Теореманы логикалық-дидактикалық талдау және оны оқытудың әдістемесі



Курстық жұмыс

Тақырыбы:
Теореманы логикалық дидактикалық талдау және теоремамен жұмыс істеу әдістемесі

Жұмыстың негізгі мақсаты:
Теоремаға логикалық дидактикалық талдау жасау;
Теореманы және оны дәлелдеуді оқытудың, оқушының пәнге деген қызығушылығын арттырудың жолдарын қарастыру;

Жұмыстың алдына қойылған нақты міндеттер:
Теорема ұғымын, оның құрамын ашу;
Теоерманың түрлерін ажырату;
Теореманы дәлелдеу әдістерін ашып көрсету;
Теореманы оқытудың әдістемесін беру;
Оқушыларды дәлелдеуді үйретудің әдістемесін беру.

1. ОЙЛАУ ФОРМАЛАРЫНЫҢ НЕГІЗДЕРІ
КІРІСПЕ
2. ТЕОРЕМАНЫ ДӘЛЕЛДЕУ ӘДІСТЕРІ
3. ТЕОРЕМАНЫ ОҚЫТУДЫҢ ӘДІСТЕМЕСІ
ҚОРЫТЫНДЫ
Мазмұны

Пікір деп белгілі бір нәрселерге немесе құбылыстарға, олардың қасиеттеріне, байланыстарына және қатынастарына сәйкес ұйғарым мақұлданатын болмаса, теріске шығарылатын ойлау формасын айтады. Пікір ақиқат немесе жалған болуы мүмкін. Математикада пікір сөз немесе символ түрінде өрнектеледі.

Аксиома деп ешбір дәлелдеусіз қабылданатын сөйлемді айтады.
Математикалық пікірдің негізгі түрлері
Постулат дегеніміз - белгілі бір ұғым немесе үғымдардың арасындағы белгілі бір қатынас қанағаттандыруға тиісті талаптарды сипаттайтын математикалық сөйлем.

Теорема дегеніміз - ақиқаттығы дәлелдеу арқылы тағайындалатын математикалық сөйлем.
Теорема құрамы:
түсіндірме бөлігі,
теорема қарастырылатын ұғымдар жиыны,
шарты(А),
қорытындысы(В),
логикалық байланысы.

Теореманың тұжырымын логикалық тілде былай жазады: А(шарт) В(қорытынды) .

Теореманың логикалық - математикалық талдауы:
тұжырым түрі анықталады;
егер қажет болса тұжырымды импликация түріне ауыстыру;
теореманың құрылымын жазу, яғни теореманың түсіндірме бөлігін, шартын, қорытындысын және құрылымдық элементтерін белгілеу;
теореманың түрін анықтау (жай немесе күрделі) ;
теоремаға кері, қарама-қарсы және кері теоремаға қарама-қарсы теоремаларды жазу және оның ақиқаттығын немесе жалғандығын анықтау.
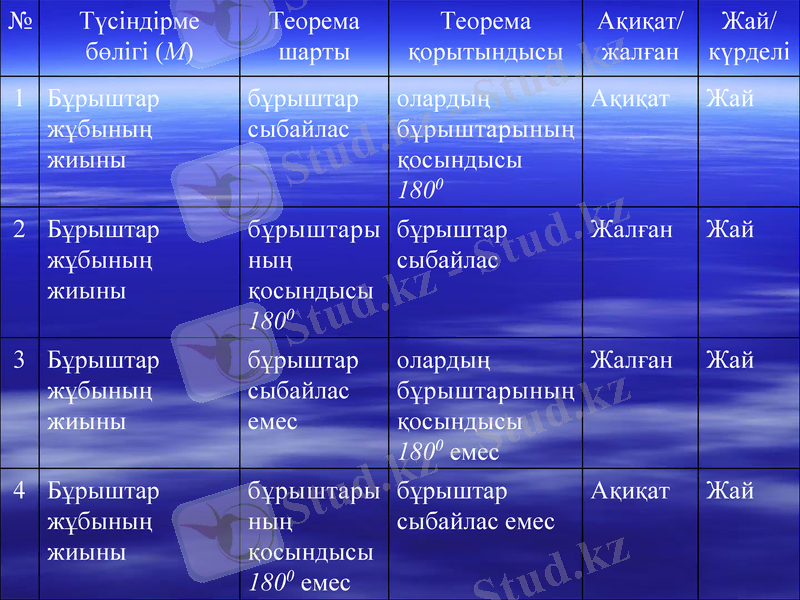
№
Түсіндірме бөлігі (М)
Теорема шарты
Теорема қорытындысы
Ақиқат/ жалған
Жай/ күрделі
1
Бұрыштар жұбының жиыны
бұрыштар сыбайлас
олардың бұрыштарының қосындысы 1800
Ақиқат
Жай
2
Бұрыштар жұбының жиыны
бұрыштарының қосындысы 1800
бұрыштар сыбайлас
Жалған
Жай
3
Бұрыштар жұбының жиыны
бұрыштар сыбайлас емес
олардың бұрыштарының қосындысы 1800 емес
Жалған
Жай
4
Бұрыштар жұбының жиыны
бұрыштарының қосындысы 1800 емес
бұрыштар сыбайлас емес
Ақиқат
Жай

Теоремалардың жалпы түрі мынадай:
1) «Егер А бар болса, онда В болады» - тура теорема.
2) «Егер В бар болса, онда А болады» - кері теорема.
3) «Егер А жоқ болса, онда В жоқ болады» - қарама-қарсы теорема.
4) «Егер В жоқ болса, онда А жоқ болады» - кері теоремаға қарама-қарсы теорема.

Теоремамен жұмыс істеу келесі кезеңдерді қамтиды:
1) Нөлдік кезең - логикалық - математикалық талдау жасау;
2) Бірінші кезең - дайындық кезеңі:
- білімді белсендендіру;
- дәйекті оқудың қажеттігін уәждеу;
- теориялық дәйекке көшу;

3) Екінші кезең - негізгі:
- теореманы тұжырымдау;
- тұжырыммен жұмыс, егер қажет болса импликация түріне көшу, шарты мен қорытындысын ажырату;
- дәлелдеудің қажеттілігін уәждеу;
- шарты мен қорытындысын талдау, дәлелдеу әдісін таңдау, дәлелдеудің схемасын немесе дәлелдеу үлгісін құру;
- дәлелдеумен жұмыс: жалпы құрылымы мен дәлелдеу қадамдарын белгілеу, дәлелдеудің аргументі мен демонстрациясын жүргізу;
- қорытынды шығару.
4) Үшінші кезең - бекіту, яғни теореманың тікелей қолданылуы (аргумент ретінде оқылған теорема ғана қолданылады және дәлелдеу 1-2 қадамдарды ғана қамтиды) .

Қажетті және жеткілікті шарттар.
АВ теоремасында шарты мен қорытындысының арасындағы байланыс әртүрлі сипатта болуы мүмкін.
Егер АВ (тура теорема, дұрыс), онда теореманың А шарты жеткілікті шарт;
Егер ВА (кері теорема, дұрыс), онда теореманың А шарты қажетті шарт;
Егер АВ (тура да, кері де, дұрыс), онда теореманың А шарты қажетті және жеткілікті шарт болады.

Теореманы дәлелдеу үш кұрамдас бөліктен турады:
1) Тезис - дәлелденетін қағида;
2) Аргумент - ақиқаттығы бұрын дәлелденген немесе тексерілген және тезистің ақикаттығы не жалғандығы негізделетін пікір;
3) Демонстрация немесе дәлелдеу тәсілі - дәлелденген тезистің ақиқаттығын түйіндейтін логикалық талқылау. Басқаша айтқанда, демонстрацияны дәлелдеу кезінде пайдаланылатын логикалық ережелердің тобы ретінде түсінуге болады.

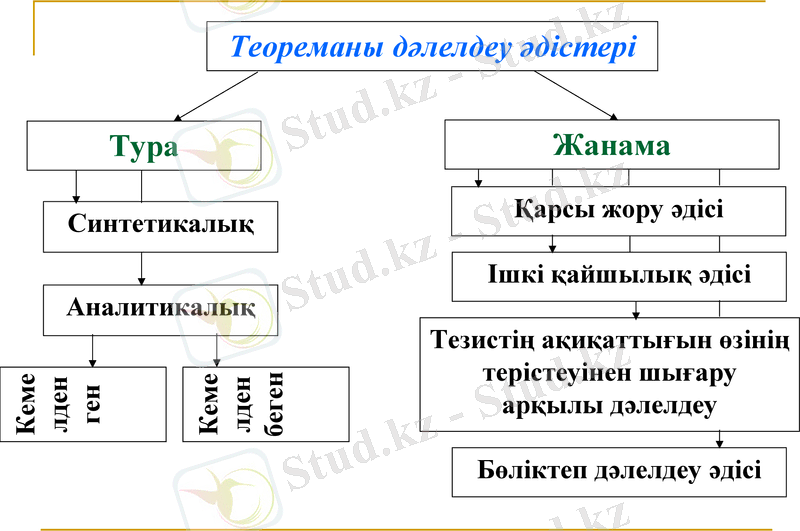
Қарсы жору әдісі

Курстық жұмыста қаралған теореманы дәлелдеу әдістері:
Дәлелдеудің дедуктивтік әдісі
Дәлелдеудің синтетикалық әдісі
Дәлелдеудің аналитикалық әдісі
Математикалық индукция әдісі
Дәлелдеуді қайшылыққа келтіру әдісі
Даралап көшіру әдісі
Векторлық әдіс

Математикалық индукция әдісі
Математикалық индукция принципі:
Егер n натурал санынан тәуелді қандай да бір P(n) математикалық сөйлемі
1) n=1 үшін дұрыс,
2) n=k үшін дұрыстығынан келесі n=k+1 саны үшін де дұрыс,
онда P(n) сөйлемі кез келген n натурал саны үшін дұрыс.

Бұл тұжырым символ түрінде мына формуламен жазылады:
P(1) kN [P(k) P(k/) ] n[P(n) ], k/=k+1;
P(n) - индукциялық сөйлем;
n - индукция жүргізілетін индукциялық айнымалы;
P(1) - индукция базисі;
P(k) P(k/) - индукциялық қадам.

Математикалық индукция әдісі арқылы дәлелдеу міндетті түрде екі бөлімнен тұрады:
1) n=1 болғандағы P(n) сөйлемінің шындығын тексеру, яғни P(1) ;
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz