Алғашқы функция және интеграл: қисық сызықты трапецияның аудандарын есептеуді бекіту және бағалау

« Мойынқұм ауданы әкімдігі білім бөлімінің Қ. Рысқұлбеков атындағы орта мектебі» мемлекеттік мекемесі .

Математика және информатика пәнінің мұғалімі

Таткеева Гүлжан Мырзахметқызы

Сабақтың тақырыбы: «Алғашқы функция және интеграл» тарауын бекіту.

Сабақтың мақсаты:

1. Қисық сызықты трапецияның ауданын табу, Нюьтон-Лейбниц формуласы және интегралдың көмегімен жазық фигуралардың аудандарын табу тақырыптырын оқушылардың қаншалықты меңгергендігін тексеру, бекіту және бағалау.

2. Оқушының ой -өрісін, сана-сезімін қалыптастыру, шығармашылық қабілетін дамыту.

3. Оқушыларды алғырлыққа, шапшаңдыққа және тапқырлыққа тәрбиелеу.

Сабақтың типі: Бекіту және бағалау сабағы.

Сабақтың әдісі: Топпен жұмыс.

Сабақтың көрнекілігі: әр түрлі графиктер сызылған плакаттар.

Сабақтың барысы:

1. Ұйымдастыру кезеңі.

2. Сабақтың мақсатын қою.

3. Білімді бекіту және бағалау.

а) Ауызша жұмыс («Ой шақыру» стратегиясы ) .

ә) Жұппен жұмыс («Миға шабуыл» стратегиясы) .

б) Тесттік формада берілген жаттығулар. ( «Ой толғаныс» стратегиясы)

4. Үйге тапсырма беру.

Бағалау парағы.

р/с

Оқушының аты-жөні

Ауызша жұмыс

Жұппен жұмыс

Тест тапсырмасы

Бағасы

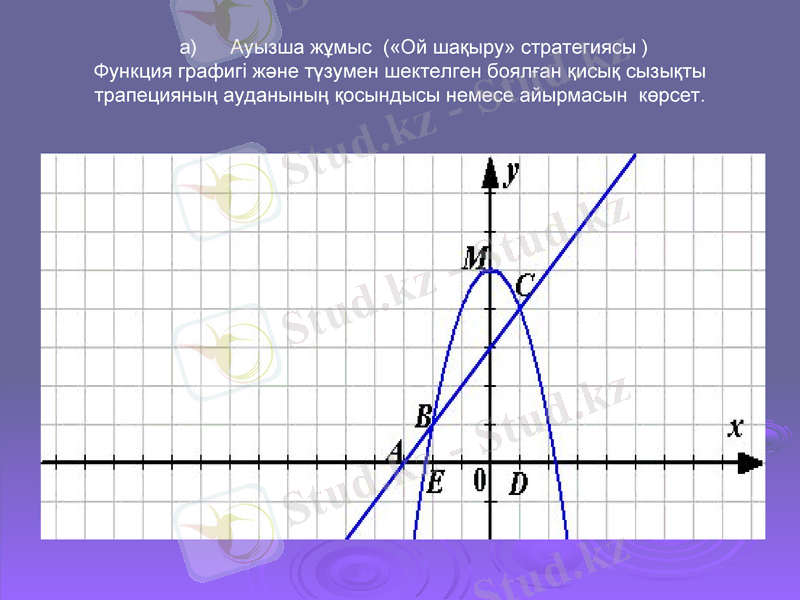
а) Ауызша жұмыс («Ой шақыру» стратегиясы )

Функция графигі және түзумен шектелген боялған қисық сызықты трапецияның ауданының қосындысы немесе айырмасын көрсет.

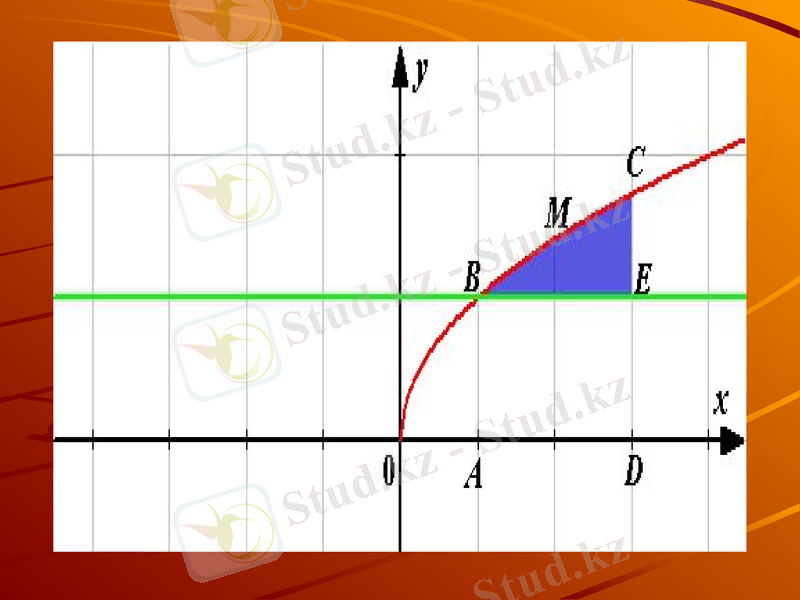
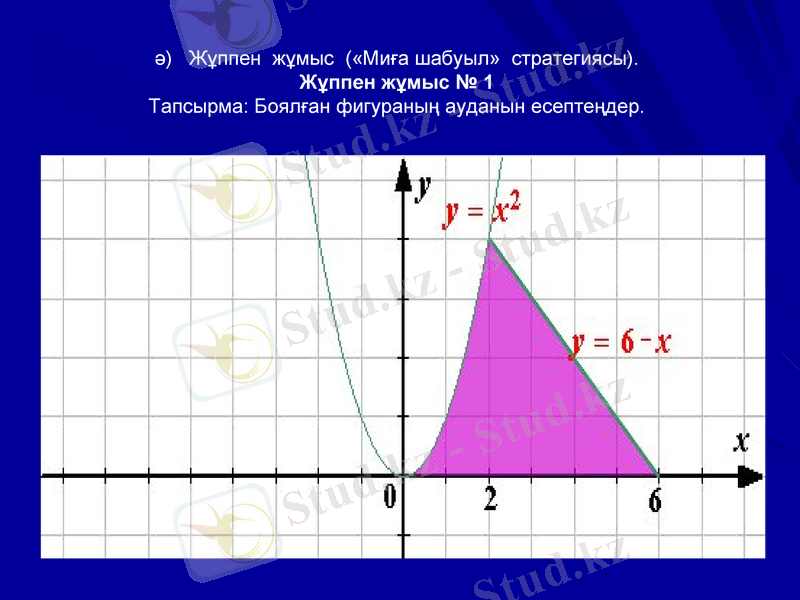
ә) Жұппен жұмыс («Миға шабуыл» стратегиясы) .

Жұппен жұмыс № 1

Тапсырма: Боялған фигураның ауданын есептеңдер.

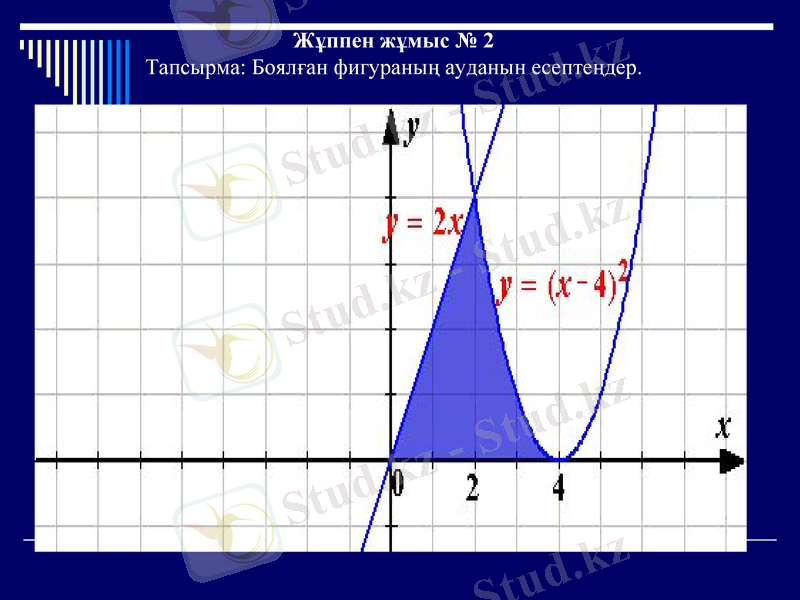
Жұппен жұмыс № 2

Тапсырма: Боялған фигураның ауданын есептеңдер.

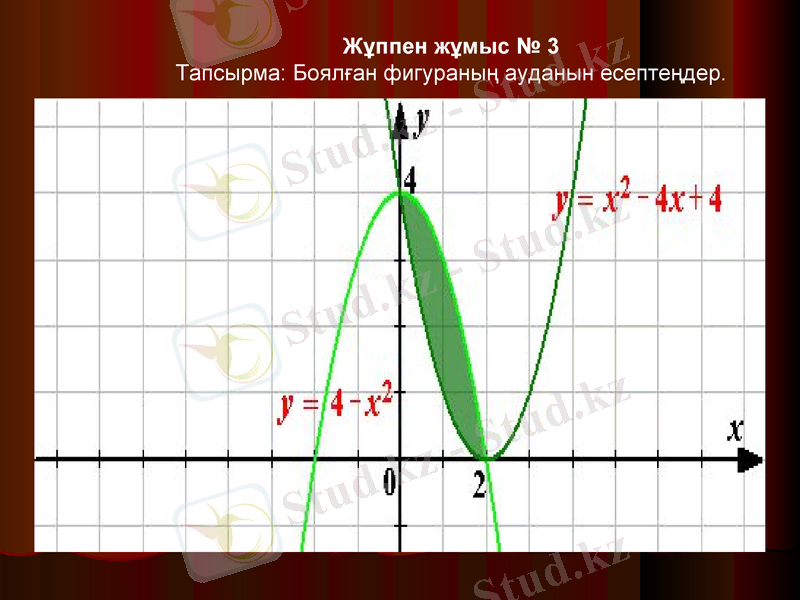
Жұппен жұмыс № 3

Тапсырма: Боялған фигураның ауданын есептеңдер.

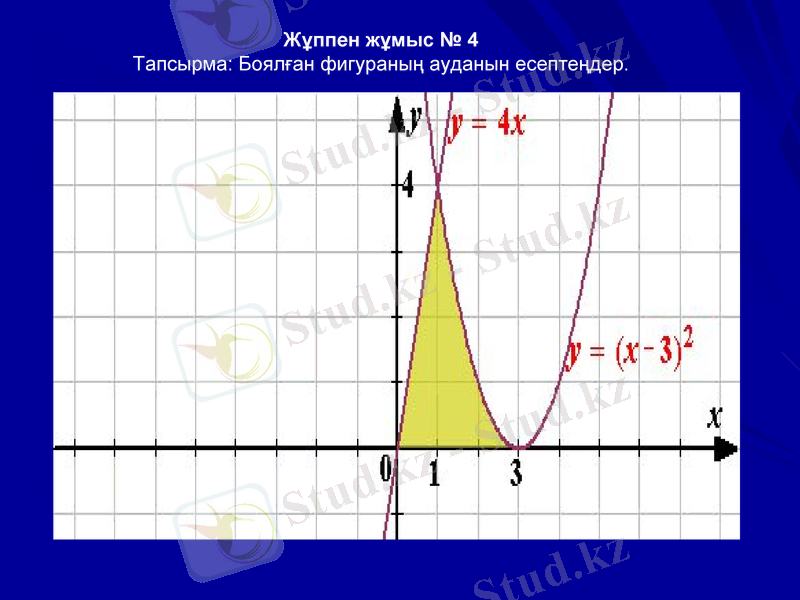
Жұппен жұмыс № 4

Тапсырма: Боялған фигураның ауданын есептеңдер.

б) Тесттік формада берілген жаттығулар. ( «Ой толғаныс» стратегиясы) .

Мына F(х) = 2х + х³ функциясы төмендегі функциялардың қайсысына алғашқы функция болады:

1) f(х) = 2 + х³;

2) f(х) = х3 +

х4;

3) f(х) = 2 + 3х².

функциясына төмендегі функциялардың қайсысы алғашқы функция болады:

, 2)

, 3)

Интегралды есепте:

. Жауабы: 1)

; 2)

; 3)

)

. Жауабы: 1)

; 2)

; 3)

Тапсырма: Мына сызықтармен шектелген фигураның ауданын есепте:

№ 1. у = 2х, у = 0, х = 0, х = 1. 1) 1; 2) 2; 3) 3; 4) 4.

№ 2. у = 2 - х3, у = 1, х = -1, х = 1. . 1) 1; 2) 2; 3) 3; 4) 4.

№ 3. у = 5 - х2, у = 2х2 + 1, х = 0, х = 1. . 1) 1; 2) 2; 3) 3; 4) 4.

№ 4. у = 2sin x, х = 0, х = p, у = 0. . 1) 1; 2) 2; 3) 3; 4) 4.

№ 5. у = 2х - 2, у = 0, х = 3, х = 4. . 1) 5; 2) 6; 3) 3; 4) 4.

№ 6. у = 3х2 + 2, у = 0, х = -1, х = 1. . 1) 1; 2) 3; 3) 5; 4) 6.

10.

Тест жауаптары

1. 3

2. 1

3. 2

4. 3

5. 1

6. 2

7. 3

8. 4

9. 5

10. 6

Үйге тапсырма беру.

у =

функециясы үшін алғашқы функцияның жалпы түрін анықтаңдар

2. Интегралды есепте

3. Мына сызықтармен шектелген қисық сызықты трапецияның (алдын ала суретін салып алып) ауданын есепте:

у = cos x, у =0, х =

, х =

4. Мына сызықтармен шектелген фигураның ауданын есепте:

у = х2 - 1 және у = 1 - х2 .

Ұқсас жұмыстар

Алғашқы функция және интеграл: пысықтау сабақ жоспары, есептер және бағалау

Алғашқы функция және интеграл: анықтамалар, негізгі формулалар және есептер

Алғашқы функция және интеграл: 11-сынып математика сабағының жоспары мен жаттығулары

Алғашқы функция мен анықталмаған интеграл: теория және есептер

Қисық сызықты қозғалыс және шеңбер бойымен бірқалыпты қозғалыстың сипаттамасы

Қисық сызықты қозғалыс: шеңбер бойымен бірқалыпты қозғалыс, бұрыштық және сызықтық жылдамдық

Алғашқы функция және интегралдар: сабақ жоспары, есептер мен тест

Үш еселі интеграл: теориясы, есептеу әдістері және қолданбалары

Анықталған интеграл: есептеу әдістері мен қолданылуы

11-сынып: Интеграл арқылы фигуралардың ауданы мен айналу денелерінің көлемін есептеу

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz