Электростатика: элементар зарядты анықтау және Кулон заңын тәжірибелік тексеру; Гаусс теоремасы, диэлектриктер және конденсаторлар



Қазақстан Республикасының Бiлiм және ғылым министрлiгi Семей қаласының Шәкәрім атындағы мемлекеттік университеті Физика-математика факультеті CӨЖ Тақырыбы:1. Иоффе және Милликен тәжірибесі. Элементар электр зарядың анықтау. 2. Кулон заңының әртүрлі қашықтықтар үшін тәжірибе жүзінде тексерілуі. Кавендиш әдісі. 3. Вакуумдағы кейбір электростатикалық өрістерге Гаусс теоремасын қолдану. 4. Эквипотенциал беттер. 5. Электрлік ығысу векторы және диэлектрлік өтімділік. 6. Конденсаторлар, олардың түрлері және сиымдылықтары Орындаған: Мәдениет Қ. Тексерген: Рахимбердина А. Т Тобы: Т-423 Семей, 2015 жыл

Электростатика

Жоспары
1. Электр зарядының сақталу заңы.
2. Кулон заңы.
3. Электр өрісі. Электр өрісінің кернеулілігі. 4. Кернеулік векторының ағыны.
5. Вакуумдағы электр өрісі үшін Остроградский-Гаусс теоремасы. .
6. Электр өрісінің күшінің жұмысы.
7. Циркуляция.
8. Потенциал.
9. Потенциалдық электр өрісінің кернеулігімен байланысы.

Электр зарядының сақталу заңы
Зерттеу жұмыстарында (1910-1914) американдық физик Р. Милликен (1868-1953) электр зарядының дискретті, яғни кез келген дененің заряды q элементар электр зарядынан тұратынын көрсетті.
e =1, 6∙10-19 Кл
me=9, 11∙10-31 кг

Электр зарядының өлшем бірлігі - кулон (Кл) - бұл ток күші 1 А болғанда, өткізгіштің көлденең қимасынан 1 с уақытта өтетін электр заряды.
Кез келген тұйық жүйеде барлық бөлшектер зарядтарының алгебралық қосындысы өзгеріссіз қалады .

Кулон заңы

Электростатикалық өріс. Электростатикалық өрістің кернеулігі.
Вакуумдағы нүктелік заряд өрісінің кернеулігі
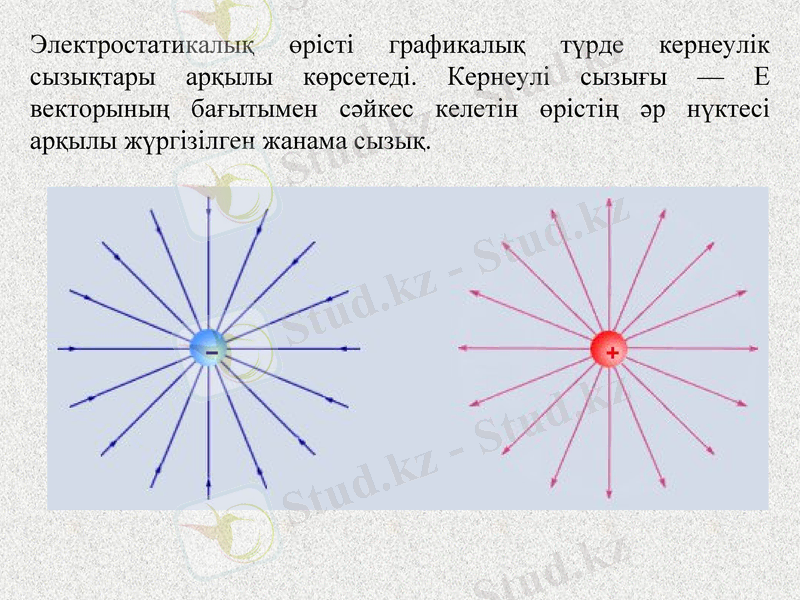
Электростатикалық өрісті графикалық түрде кернеулік сызықтары арқылы көрсетеді. Кернеулі сызығы - Е векторының бағытымен сәйкес келетін өрістің әр нүктесі арқылы жүргізілген жанама сызық.
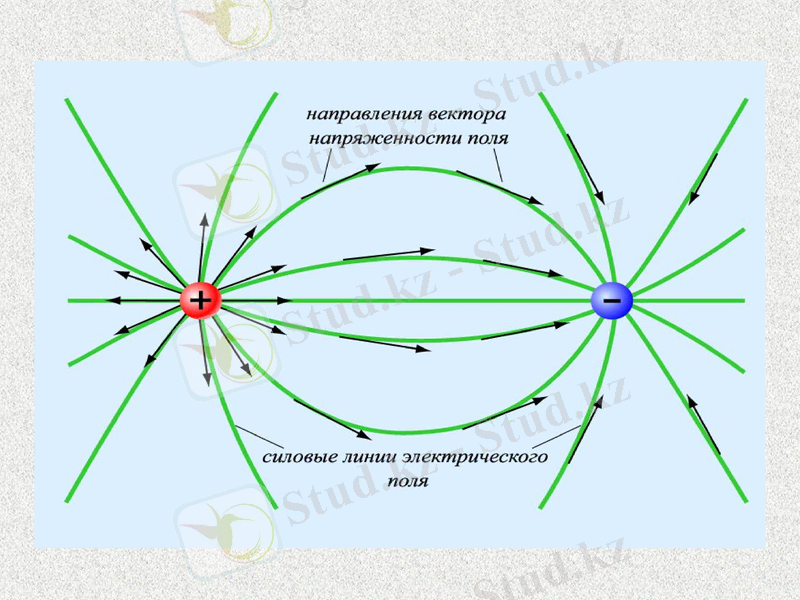

Егер өріс бірлік зарядтан турса, онда кернеулік сызықтары - түзу, егер оң заряд болса, зарядтан шығады, егер теріс заряд болса, сол зарядқа кіреді.
Суперпозиция принципы
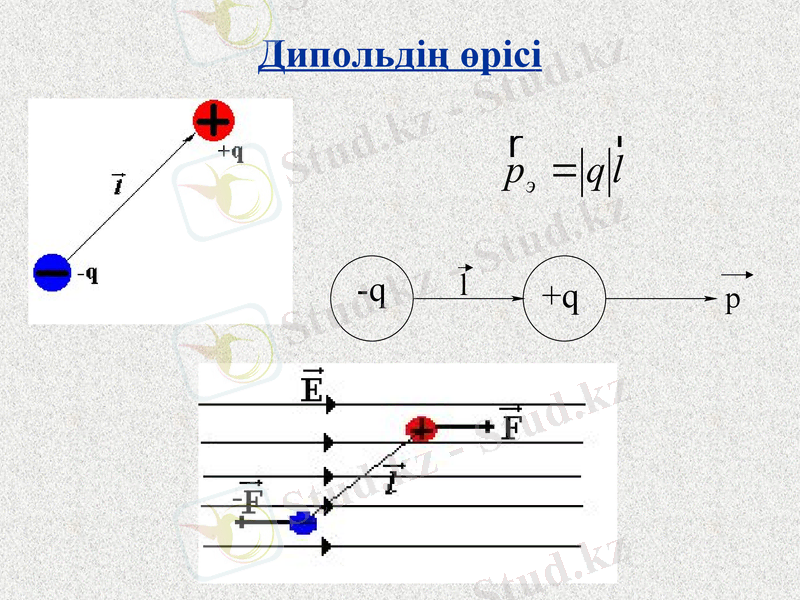
Дипольдің өрісі
-q
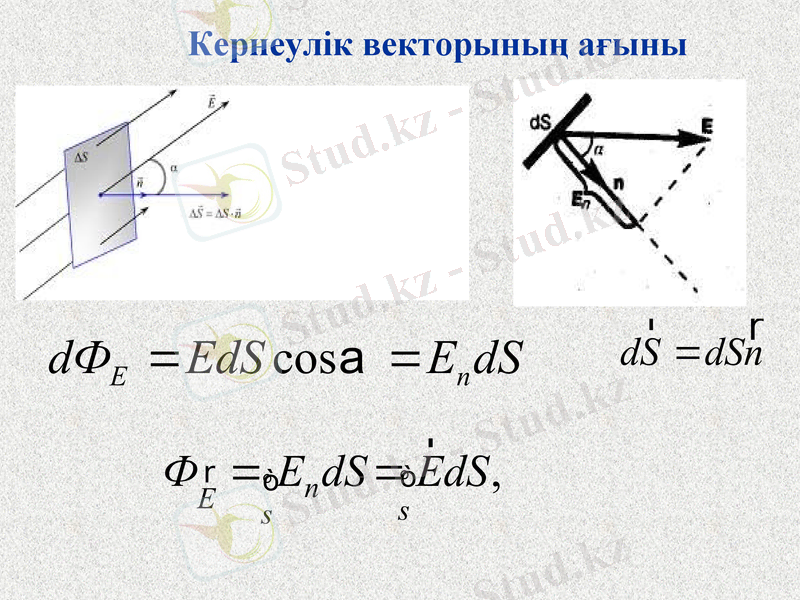
Кернеулік векторының ағыны
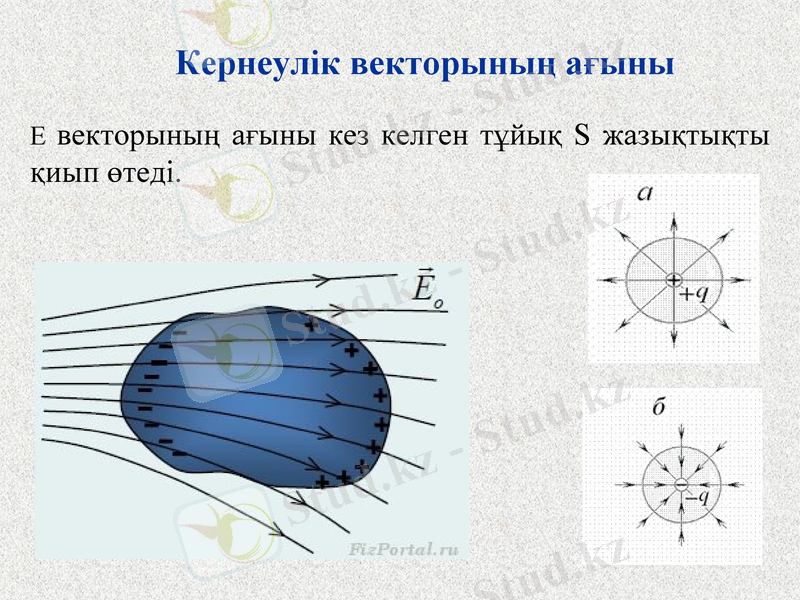
Е векторының ағыны кез келген тұйық S жазықтықты қиып өтеді.
Кернеулік векторының ағыны

Кернеулік векторының ағыны

Вакуумдағы электростатикалық өріс үшін Гаусс теоремасы
Тұйық және нүктелік q зарядтан тұратын кез келген формадағы жазықтық үшін Е векторы q/ε0 тең болады, яғни
Ағынның таңбасы q зарядының таңбамен сәйкес келеді.
К. Гаусс теоремасы кез келген тұйық жазықтық арқылы өтетін злектр өрісінің кернеулік векторының ағынын анықтайды.

Гаусса теоремасын мына түрде жазуға болады:

Кейбір вакуумдағы электростатикалық өрістерді есептеу үшін Гаусс теоремасын қолдану.

Біртекті зарядталған шексіз жазықтық өрісі.

Екі шексіз өзара параллель зарядталған жазықтықтардың өрісі
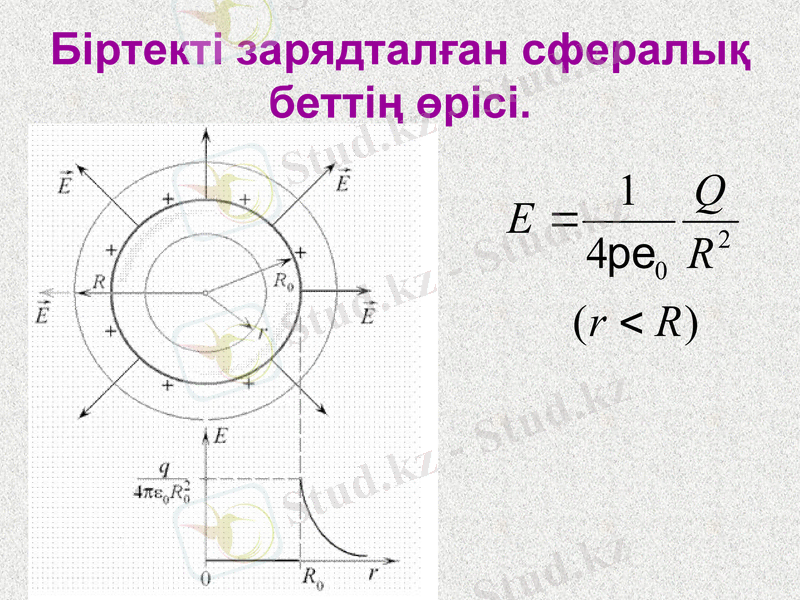
Біртекті зарядталған сфералық беттің өрісі.
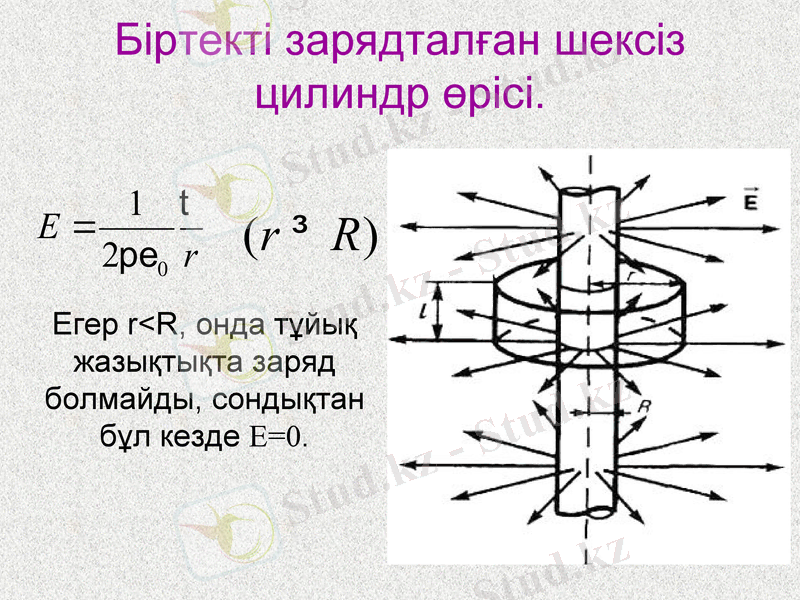
Біртекті зарядталған шексіз цилиндр өрісі.
Егер r
Электростатикалық өріс потенциалдық болып табылады.
Электростатикалық өріс күшінің жұмысын q зарядының өрісінің бастапқы және соңғы нүктелеріндегі q0 нүктелік зарядтың потенциалдық энергиясының айырымы ретінде көрсетуге болады :
1 нүктесінен 2 нүктесіне орын ауыстырған q0 зарядтың өріс күшінің жұмысы мына түрде де жазыла алады:
A12=Ep1- Ep2=q0(φ1 - φ2) .
Сонымен қатар 1 нүктесіне 2 нүктесіне электростатикалық өріс күшінің әсерінен орын ауыстырған q0 зарядтың жұмысы мына түрде беріле алады :
Бағытталған электростатикалық өрістің кернеулік векторының циркуляциясы:
Электр өріс потенциалы
Электр өрісінің кернеулігі мен φ потенциал арасындағы байланыс.
Декарттық координат жүйесінде:
Егер өріс біртекті және Х осі бойымен бағытталса, онда:
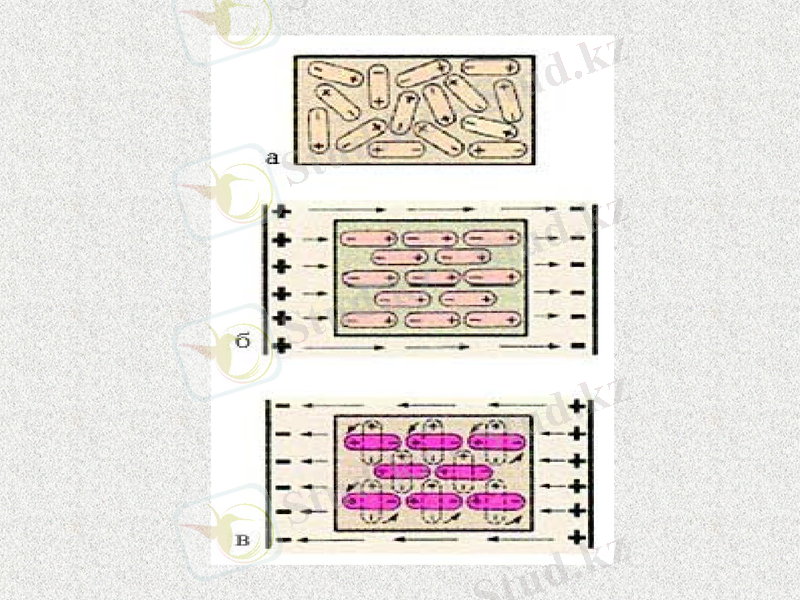
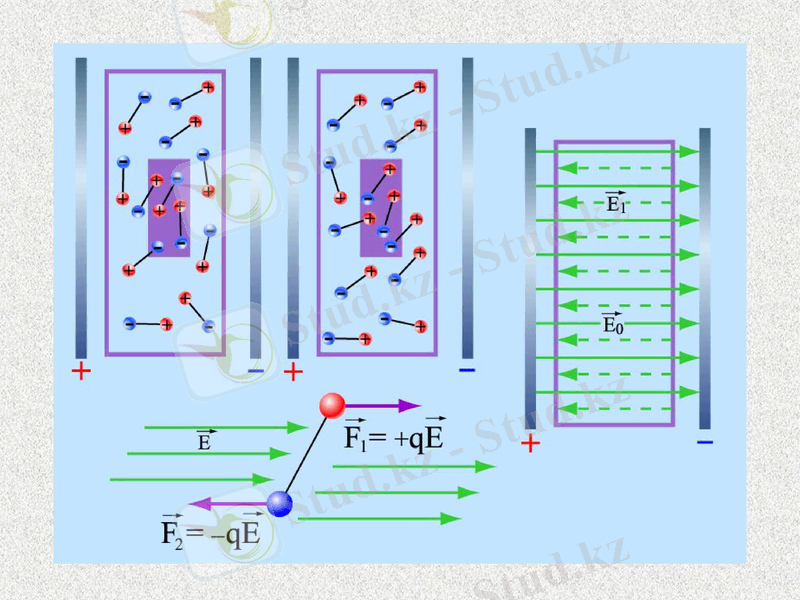
Диэлектриктердің түрлері
P=æε0Ε
ε = 1+æ
Электр ығысу векторы
Диэлектриктегі электростатикалық өріс үшін Гаусс теоремасы
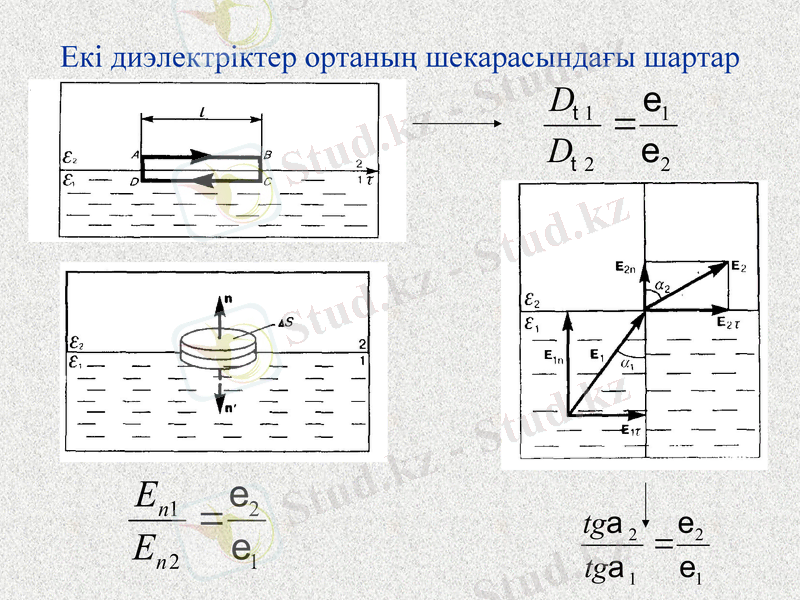
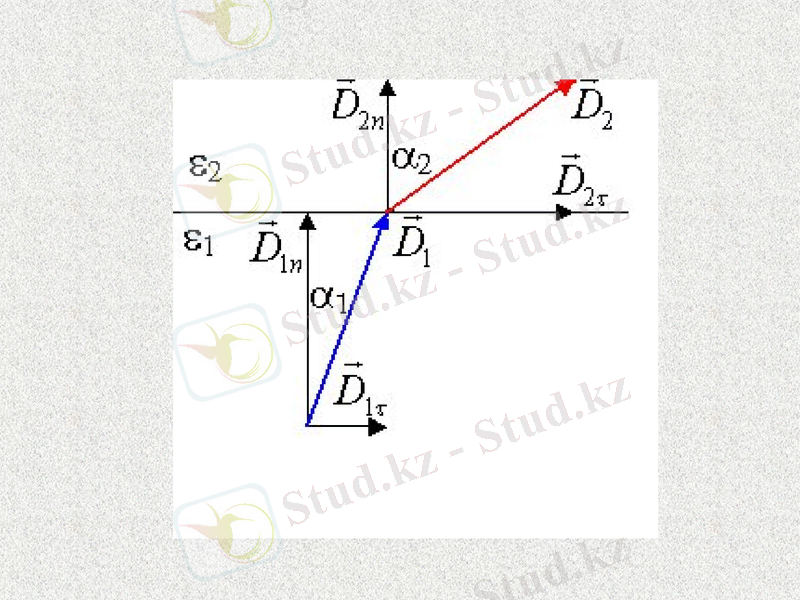
Екі диэлектріктер ортаның шекарасындағы шартар
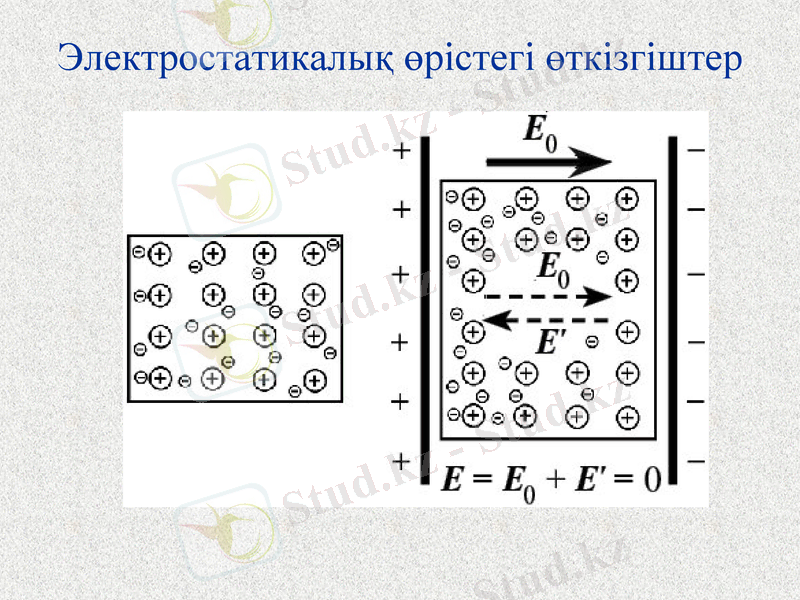
Электростатикалық өрістегі өткізгіштер
Электро сыымдылық
Конденсаторлар
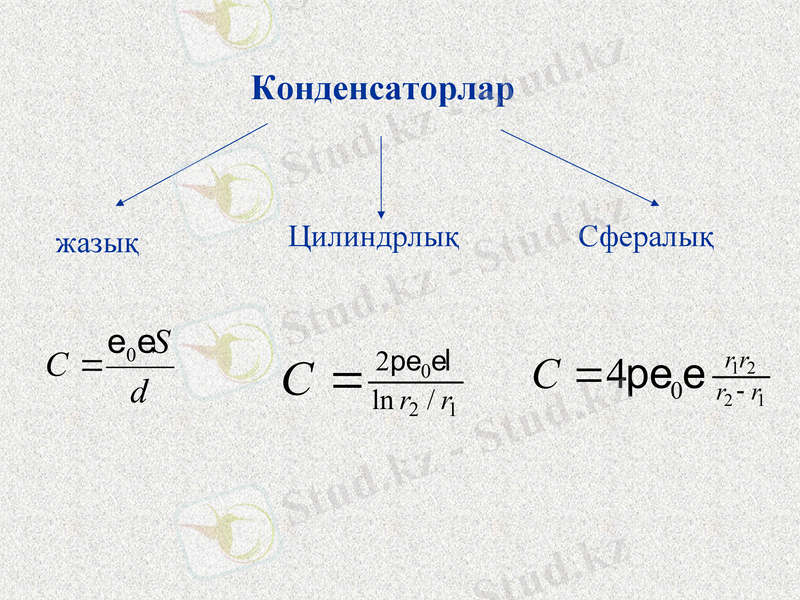
Конденсаторлар
жазық
Цилиндрлық
Сфералық
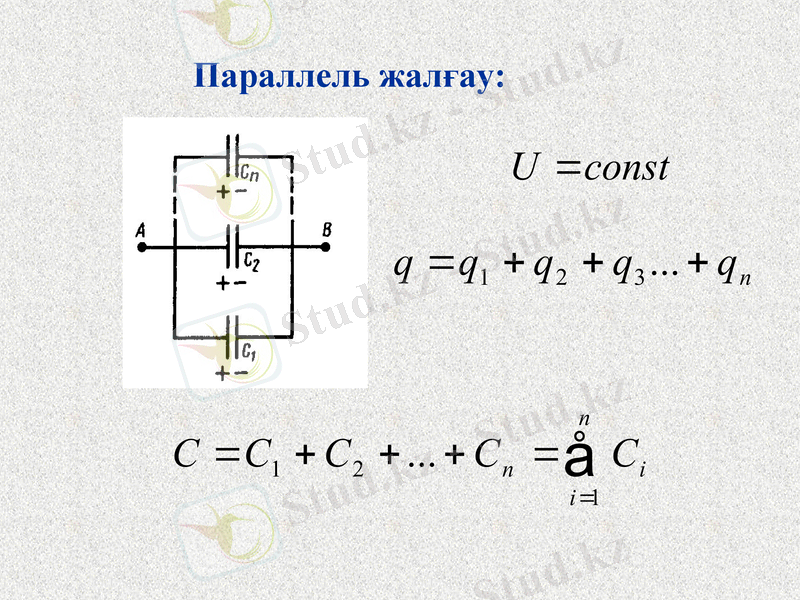
Параллель жалғау:
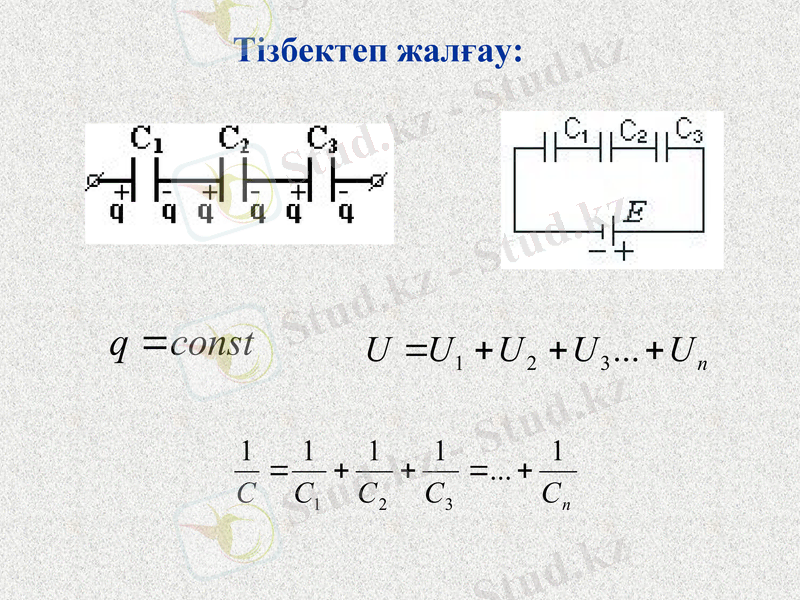
Тізбектеп жалғау:
Электростатикалық өріс энергиясы
Назарларыңызға рахмет!!!













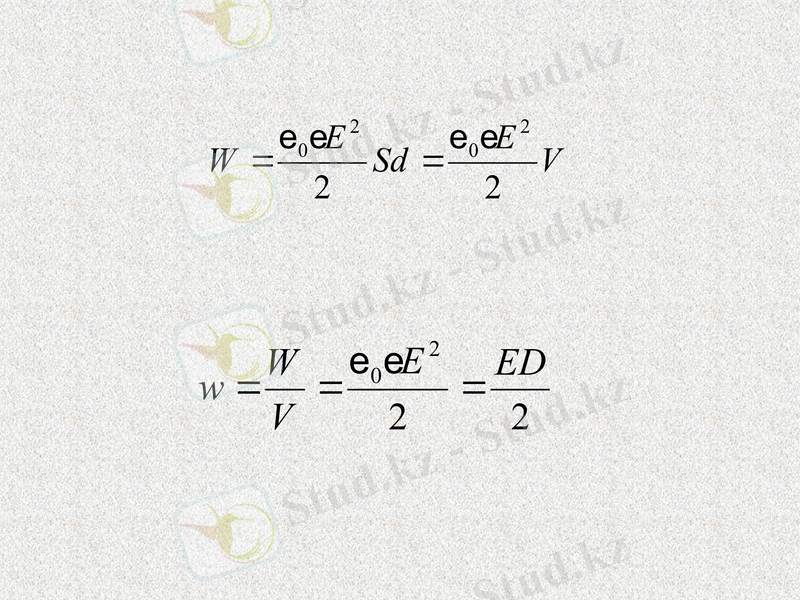

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz