Ықтималдық теориясының басты түсініктері және теоремасы. Моменттер. Дисперсия. Орташа квадраттық ауытқулар

Презентация қосу

ТЕОРИЯСЫНЫҢ
БАСТЫ ТҮСІНІКТЕРІ
ЖӘНЕ ТЕОРЕМАСЫ.
МОМЕНТТЕР.
ДИСПЕРСИЯ.
ОРТАША
КВАДРАТТЫҚ
АУЫТҚУЛАР
ЖОСПАР
I. Кіріспе
II. Негізгі бөлім
а) Ықтималдықтар теориясының
өмірде кездесуі.
b) Ықтималдықтар теориясының
тарихына шолу.
c) Зерттеу бөлімі.
d)Теория ғылыми тұрғыдан.
e) Моменттер
III. Қорытынды
Ықтималдықтар теориясы өз бастауын XVII ғасырдан
алады.Алдымен азартты ойындар пайда болды.Араб тілінде
«азар» деген сөз «қиын» деген мағына береді.Арабтар «азар»
деп лақтырылған ойын сүйегінің екеуінде де 6 ұпайдан түсүін
айтады екен.Куб түріндегі ойын құралы ол кезде піл сүйегінен
жасалатын болғандықтан «ойын сүйегі» деген атау сол
заманнан қалыптасып қалған.Ықтималдықтар теориясы
жөніндегі алғашқы жұмыстар XVII ғасырда басталды. Еуропа
елдерінде адамды құнықтыратын әр түрлі ойындардың кең
таралуына байланысты әр ойыншы өзінің жеңілмеу
ықтималдықдығын алдын ала анықтауға тырысты.Сол кездегі
математиктер де бұл мәселеге назар аудардып,бірнеше рет
қайталанатын кездейсоқ оқиғалар туралы заңдылықтар ашу ға
талпынды.Бұл мәселеге алғашқы болып еңбектерін
ұсынған:француз оқымыстысы Блез Паскаль,Пьер
Ферма,голландиялық Христиан Гюйгенс,швецариялық
математик Яков Бернулли болды. Француздың атақты
математиктері Пьер Ферма мен Блез Паскальдың азартты
ойындар жөніндегі зерттеулері ықтималдықтар теориясыны ң
негізін қалады.
1. Тәжірибе – өмірде
жүргізілетін белгілі бір
бақылаулар. Белгілі бір
шарттарды өзгертпей,
тәжірибені қайталауға
болады.
ТӘЖІРИБЕ
МЫСАЛДАРЫ
Элементар жиын –
тәжірибе нәтижесінде
пайда болатын жиын
Кездейсоқ оқиға –
элементар оқиғалардан
тұратын күрделі оқиға
Кездейсоқ оқиға – болуы да
болмауы да мүмкін оқиға
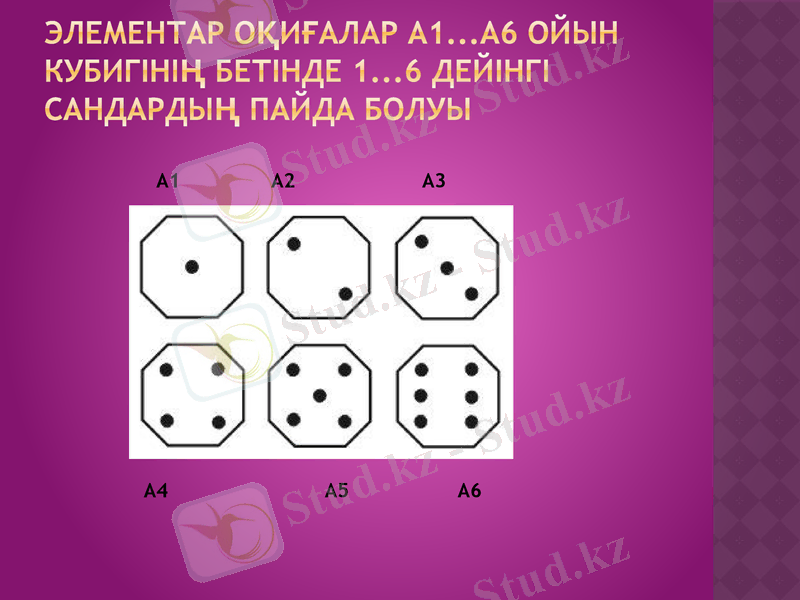
ЭЛЕМЕНТАР ОҚИҒАЛАР А1...А6
ОЙЫН КУБИГІНІҢ БЕТІНДЕ 1...6
ДЕЙІНГІ САНДАРДЫҢ ПАЙДА
БОЛУЫ

А1 А2 А3

А4 А5 А6
Ақиқат оқиға –
тәжірибе нәтижесінде
пайда болатын оқиға
Мүмкін емес оқиға –
тәжірие нәтижесінде
пайда болмайтын
оқиға
КЕЗДЕЙСОҚ ОҚИҒАЛАР
Егер бір ғана тәжірибенің барысында
бір нәтиженің пайда болуы екінші
нәтиженің пайда болуын жоққа
шығарса, онда бұл оқиғаларды өзара
үйлесімсіз деп атайды
Мысалы

А В
Егер жүргізілген тәжірибенің
нәтижесінде бірнеше оқиғаның ең
болмағанда біреуі пайда болса, ондай
оқиғаларды толық топ құрайтын
оқиғалар деп атаймыз.
ОСЫ 2 ОҚИҒА ҮЙЛЕСІМСІЗ ЖӘНЕ
ТОЛЫҚ ТОП ҚҰРАЙДЫ

1-оқиға нысанаға оқты тигізе алмауы

2-оқиға нысанаға оқты дәл тигізуі
ЫҚТИМАЛДЫҚТЫҢ
НЕГІЗГІ АНЫҚТАМАЛАРЫ
Белгілі А оқиғасының
ықтималдығы деп, осы
оқиғаға қолайлы
жағдайлар санынынң
барлық жағдайлар
санына қатынасын
айтамыз.
Мұндағы m – барлық жағдайлар саны
n – А оқиғасына қолайлы жағдайлар саны
Кездейсоқ оқиғаның ықтималдығы
P(A)=1 болса А – ақиқат оқиға
P(A) =0 болса А – мүмкін емес оқиға
ДИСПЕРСИЯ

Кездейсоқ шама

Дискрет
Үздіксіз
ті
АУЫЗША
ТҮСІНДІРЕТІНІМ
МЫСАЛ
ТЫҢДАҒАНДАРЫҢЫЗҒА
КӨП РХМЕТ!

Ұқсас жұмыстар

Ықтималдық теориясы

Вариациялық көрсеткіштер

Ықтималдықтар теориясының негізгі түсініктері. Ықтималдық теориясын көбейту теоремасы

Өлшеулер және олардың геодезиялық және фотограмметрикалық жұмыстардағы мәні

Дисперсиялық талдау

Гетероскедастикалықты түзету тәсілдері

Қателер теориясы

Қаржылық тәуекелдерді талдау және бағалау

ОРТАША ШАМАЛАР ЖӘНЕ ВАРИАЦИЯ КӨРСЕТКІШТЕРІ

Бас жиынтық және таңдама. Таңдамалы сипаттамалар

Пәндер