Стереометрия аксиомалары және олардың қарапайым салдары

Презентация қосу

*Стереометрия
аксиомалары және олардың
қарапайым салдары
Мақсаты

O Білімділік: Оқушылардың білімге
деген қызығушылықтарын арттыру.
O Дамытушылық: есепке қызықтыру
арқылы білімін тереңдету
O Тәрбиелік: Зияткерлік қабілетін
дамыту
Ойынның мақсаты:
O
Оқушылардың бір біріне жолдастық,достық
қарым қатынастары арта түседі.
Бір - бірлеріне бар ынта -жігерлерімен
көмектесуге,үйретуге бейім болады,үйрете жүріп
өзі де үйренеді.
Бір сабақтың үстінде берілген материалдарды
толық қамтуға мүмкіндік туады.
Өз білімімен жолдастарының білімін саралай
,бағалай білулеріне.
*«Білім аукционы»
сайысына қош
келдіңіздер!!!
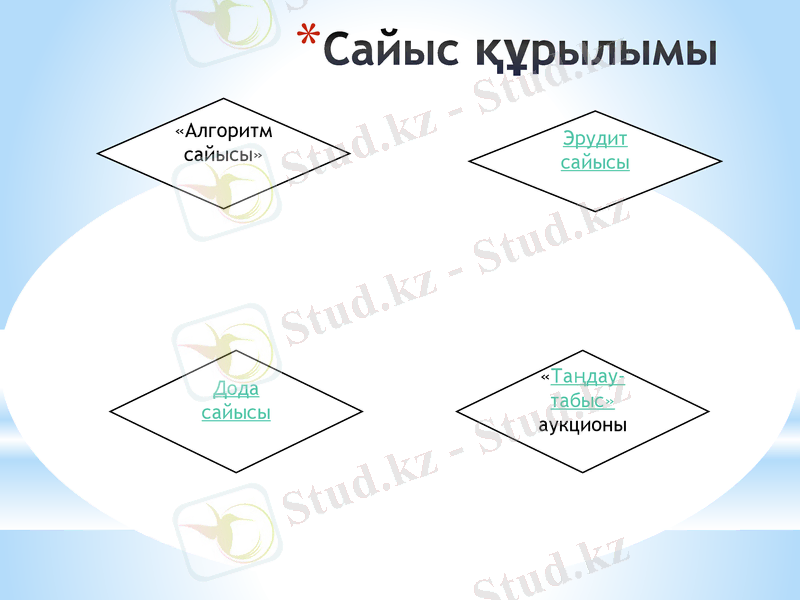
* Сайыс құрылымы
«Алгорит
м Эрудит
сайысы» сайысы

«Таңдау-
Дода
табыс»
сайысы
аукционы
«Адам байлығының
ішіндегі ең тамашасы
-білім»
Әбу-Райхан әл
Бирунидің

айтқан сөзімен алғашқы
сайысымызды бастаймыз
АЛГОРИТМ САЙЫСЫ
Ойынның жүргізілу барысы,
5 оқушыдан 4 топқа бөлеміз «А» «Б» «В» «
Г»
Берілген тапсырманы топтың бәрі
талқылайды.
Ең жоғары ұпай 10 балл, орташа балл 9
ұпай,
төмен балл 8 ұпай
Ұпай саны аз 2 топ ойыннан шығады.
1-ші «А»- тобы
O Түзудің жазықпен орналасуы
жайында айтылған аксиома

O А нүктесінде қиылысатын әр түрлі екі
түзу берілген. Берілген екі түзуді қиятын
және А нүктесінен өтпейтін барлық
нүктелер бір жазықтықта жататынын
дәлелдеңдер
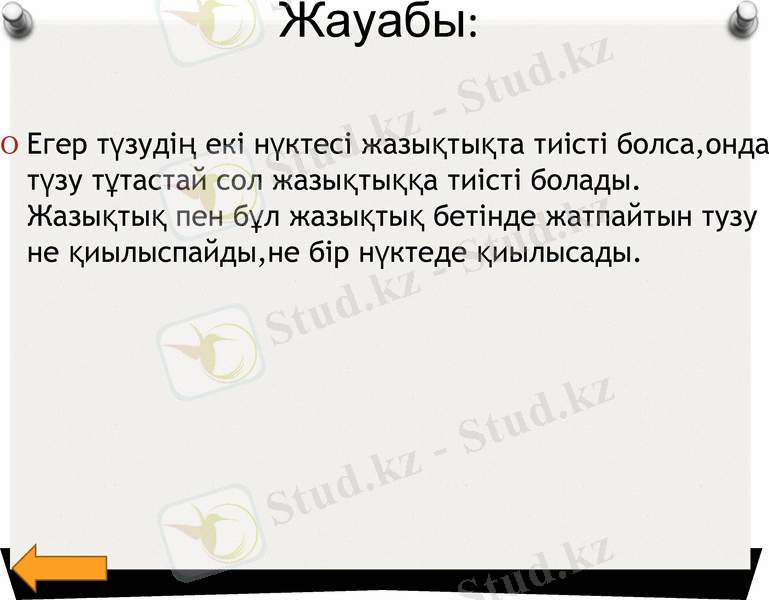
Жауабы:

O Егер түзудің екі нүктесі жазықтықта тиісті
болса,онда түзу тұтастай сол жазықтыққа
тиісті болады. Жазықтық пен бұл жазықтық
бетінде жатпайтын тузу не қиылыспайды,не
бір нүктеде қиылысады.
O Шешуі:
Берілгені: а ∩β = А В С а
а∩с=β
В ∩ с =с • •
Дәлелдеу керек: а, в, с Є α α •
Дәлелдеу керек: 1) а ∩ β арқылы С
жазықтық жүргіземіз.
2 салдар бойынша В Є α β
Сондықтан а, в, с, Є α
2-ШІ. Б-ТОБЫ
Берілген түзу және берілген нүкте арқылы
өтетін жазықтықтың бір болуы.
Түзу онда жатпайтын нүкте арқылы жазықтық
жүргізуге болады және ол тек біреу ғана
болады. Аксиоманы айт.

Берілген: түзуді қиып өтетін және сол түзуден
тысқары алынған нүктеден өтетін барлық
түзулер бір жазықтықта жататынын дәлелдеу.
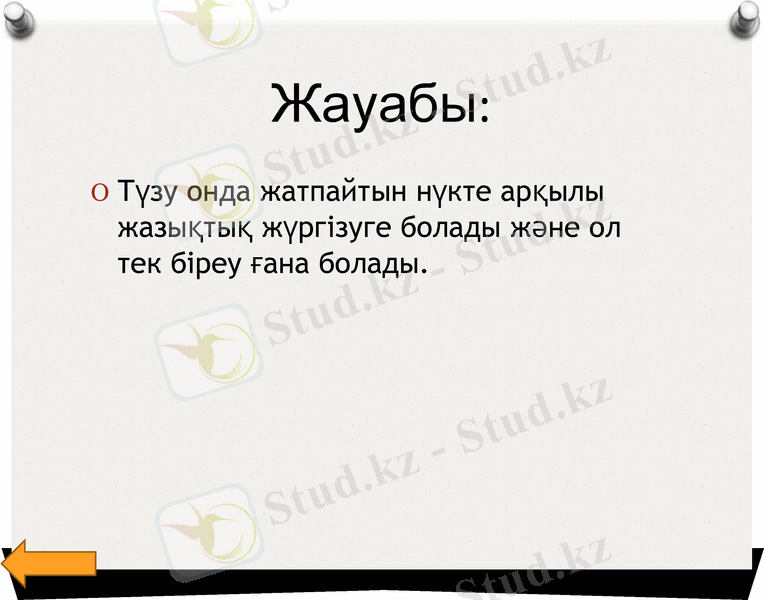
Жауабы:
O Түзу онда жатпайтын нүкте
арқылы жазықтық жүргізуге
болады және ол тек біреу ғана
болады.
O Шешуі: А Є α
АЄВ
а ∩ в =с
дәлелдеу керек: а,в Є α дәлелдеу керек
берілуі бойынша а ∩ в =с болғандықтан 3
аксиома бойынша бір жазықтық жүргізуге
болады. Сондықтан а, в Є α
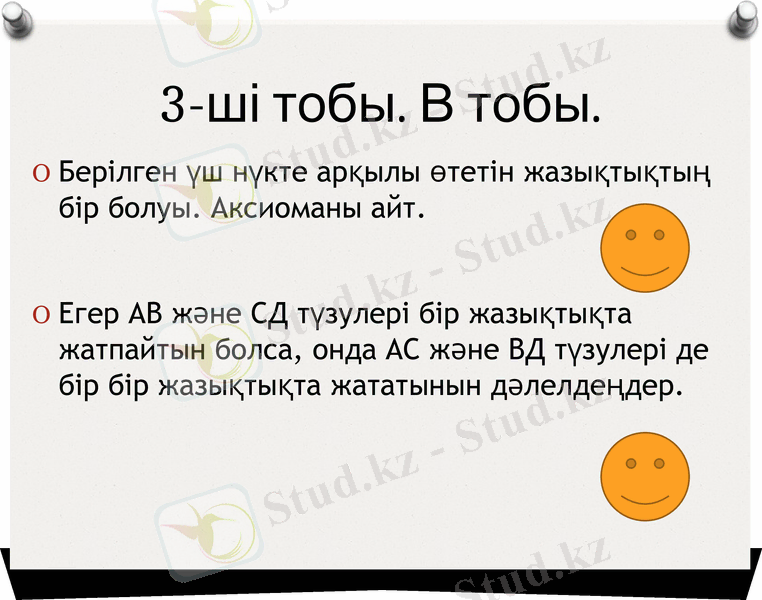
3-ші тобы. В тобы.
O Берілген үш нүкте арқылы өтетін
жазықтықтың бір болуы. Аксиоманы айт.

O Егер АВ және СД түзулері бір жазықтықта
жатпайтын болса, онда АС және ВД
түзулері де бір бір жазықтықта
жататынын дәлелдеңдер.
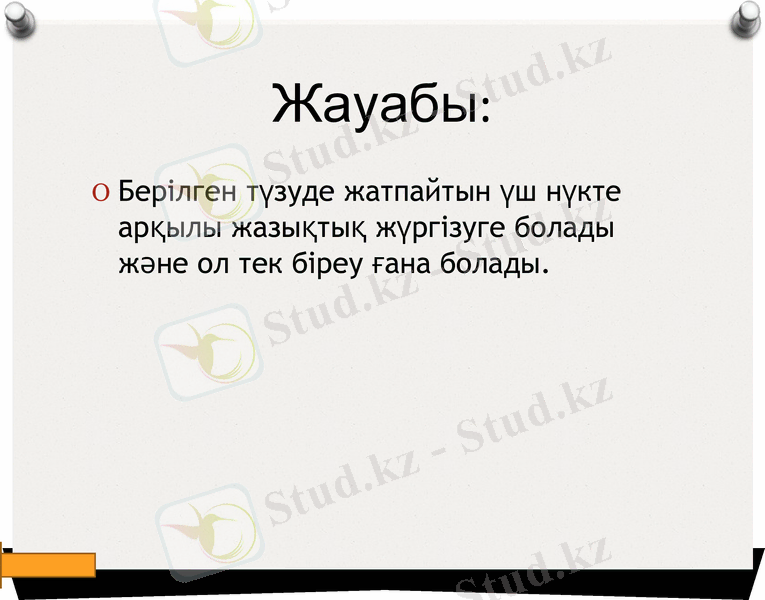
Жауабы:
O Берілген түзуде жатпайтын үш
нүкте арқылы жазықтық жүргізуге
болады және ол тек біреу ғана
болады.
O Берілгені АВ,СД Є α
Дәлелдеу керек АС,ВД Є α
Дәлелденуі: қарсы жоримыз,сонда АВ Є
ВД Є α
III- ші аксиома бойынша жүргіземіз АВСД Є
α бұл есептің берілгені қарсы,сондықтан
қарсы жорығымыз дұрыс емес.
4ші. Г тобы
O Кеңістікті екі жарты кеңістікке
жазықтықпен бөлу
Аксиоманы ата

O Бір жазықтықта жатпайтын төрт нүкте
берілген, осы нүктелердің үшеуі арқылы
өтетін әр түрлі неше жазықтық жүргізуге
болады
Жауабы:
O Жазықтықтың кеңістікті екі жарты кеңістікке
бөледі. Егер х пен у нүктелері бір жарты
кеңістікке тиісті болса,онда ху кесіндісі
жазықтықты қимайды,Егер де ХпенУ кесіндісі
жазықтықты қимайды, Егер де Х пенУ нүктелері
әр түрлі жарты жазықтықтарға тиісті
болса,онда ХУ кесіндісі жазықтықты қияды.
O Шешуі А,В,С,Д Є α
Дәлелдеу керек: α=?
Дәлелденуі: 1) (А,В,С) 3) (В,С,Д)
2) (А,С,Д) 4) (А,В,Д)
«Білім-біліктілікке
жеткізер баспалдақ, ал
біліктілік-сол білімді іске
асыра білу дағдысы»
деген Ахмет
Байтұрсынұлының
сөздеріне сүйеніп
«Эрудит» сайысын
бастайық.
ЭРУДИТ САЙЫСЫ
Берілген сұрақтарға 2 топ кезекпен жауап
береді.
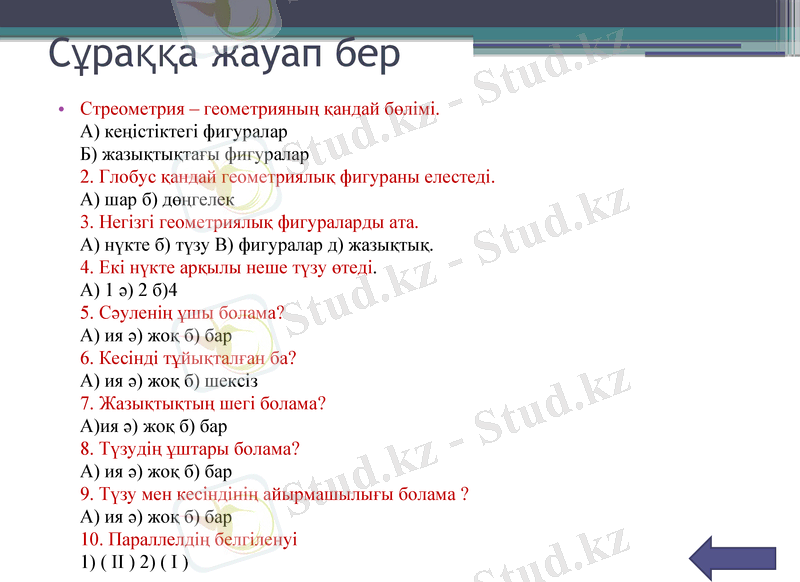
Сұраққа жауап бер
• Стреометрия – геометрияның қандай бөлімі.
А) кеңістіктегі фигуралар
Б) жазықтықтағы фигуралар
2. Глобус қандай геометриялық фигураны елестеді.
А) шар б) дөңгелек
3. Негізгі геометриялық фигураларды ата.
А) нүкте б) түзу В) фигуралар д) жазықтық.
4. Екі нүкте арқылы неше түзу өтеді.
А) 1 ә) 2 б)4
5. Сәуленің ұшы болама?
А) ия ә) жоқ б) бар
6. Кесінді тұйықталған ба?
А) ия ә) жоқ б) шексіз
7. Жазықтықтың шегі болама?
А)ия ә) жоқ б) бар
8. Түзудің ұштары болама?
А) ия ә) жоқ б) бар
9. Түзу мен кесіндінің айырмашылығы болама ?
А) ия ә) жоқ б) бар
10. Параллелдің белгіленуі
1) ( II ) 2) ( I )
«Тіл қаруы-сөз, сөз қаруы-
ой, ақылды ой, алғыр сөз-
адамның ең жоғарғы
қасиеті» деген
Ғабиден Мұстафиннің
сөзімен келесі Дода
сайысын бастайық.
ДОДА САЙЫСЫ
Сөйлемді аяқта.
• Асау тұлпар желдей ескен арынды.
Оқу менен еңбекке ...
• Ал, балақай күш жинаудан жалықпа,
Содан кейін қыран....
• Ұл-қызыңды 5жасқа келгенше,
хандай көтер, 15-келгенше құлдай
жұмса, одан соң.......
Жауабы
O сал барыңды
болып, қалықта
құрбыңдай көріп ақылдас,
сырлас
«Білекке сенген заманда
ешкімге есе бермедік,
Білімге сенер заманда қапы
қалып жүрмейік»
Абылай
ханның
сөзімен соңғы сайысымызды
бастайық.
«Таңдау- табыс»
сайысы
O Логикалық ойлау қабілеттерін
дамыту.
Сұрақ
O Бір сарайға қамалар,
Тауық, түлкі табылар.
Есеп шарты мынадай:
Аяқ пен бас саналар
Отыз аяқ жүр көп боп.
Басы 9 бір топ боп
Көрмегенмен оларды
Айыруға болады.
Түлкі нешеу қамалған,
Тауық нешеу саналған.
Жауабы:
O Шешуі:
Аяғы 30, басы 9 30-2*9=12.
12/2=6 6 түлкі, 3 тауық.
9 бас – барлығы 4 аяқты десек 36
аяқ 36-36=6
Аяқ 6/2=3 3 тауық, 6 түлкі
Сайыс аяқталды

Ұқсас жұмыстар

Аксиомалар системасының интерпретациясы

Есептер шығару. 7 сынып, Геометрия

Еркін материялдық нүктенің динамикасы

САЛУ ЕСЕПТЕРІН ШЕШУ ӘДІСТЕМЕСІ

САЛУ ЕСЕПТЕРІ

Математиканың негізгі философиялық мәселелері

Векторлық кеңістік

Орта мектепте геометрияны оқытудың жалпы әдістемелік мәселелері

Компьютерлік графика негіздері

Нүкте және түзу

Пәндер