ТЬЮРИНГ МАШИНАСЫ жә не Марковтың нормальді алгоритмы

ТЬЮРИНГ МАШИНАСЫ және Марковтың нормальді алгоритмы

Семей қаласының Шәкәрім атындағы мемлекеттік университеті

Физика - математика факультеті, математика мамандығы

Орындаған: Абдулина П. Т-311

Тексерген:Рысжанова А. С.

Семей 2015ж

Жоспар

I. Кіріспе бөлім

А) Тьюринг машинасы және Марковтың нормальді алгоритмі

II. Негізгі бөлім

А) Тьюринг машинасының құрылысы және оның тезисі, негіздемесі

Б) Марковтың норальдау принциптері және оның міндеттері

С) Марковтың нормальді алгоритмі және Тьюринг машинасының композициясы

III. Қорытынды

IV. Әдебиеттер тізімі

Алан тьюрингтің есептеуіш машинасы

Алан Мэтисон Тьюринг (ағылш. Alan Mathison Turing; 23. 06. 1912 - 07. 06. 1954) - информатиканың дамуына үлкен үлес қосқан ағылшын математигі, логигі, криптографы. 1937 жылы абстрактілі есептеу және логикалық процестерді, принципінде алдын ала жоғары дәлдікпен жүзеге асыру мүмкіндігі туды. Алгоритм ұғымын анықтаудағы алғашқылардың бірі. "Тюринг машинасы" болды, ол кейіннен өмірге келген әмбебап-цифрлы есептеу машиналарының көптеген қасиеттерін бойына жинақтады. Тюринг үйрету машинасын жасаудың аса маңыздылығын ерекше атап көрсетті, бұл машина келе-келе тәжірибе жинақтап, сыртқы ортамен істестік барысында өз "мінез-құлқын" жетілдіре түспек. Тьюринг Белоусов-Жаботинский секілді ауытқып отыратын реакцияларды болжай білді.

Белоусов-Жаботинский реакциясы ғылыми бірлестіктерге 1968 жылы ғана таныстырылған болатын. 1950 жылы Алан компьютердің жасанды зердесін сынауды көздейтін Тьюринг тестін ұсынды. Тьюринг машинасын оқу информатикаға және математикаға қызығатын оқушыларға, «Информатика» мамандығында оқитын студенттерге өте пайдалы.

Алан Мэтисон Тьюринг

(23. 06. 1912 - 07. 06. 1954)

Тьюринг машинасы

Марковтың нормальдау алгоритмі

Марковтың алгоритмді деп аталатын жүйе не модель берілген алфавиттің кез-келген кіру жолына колдануға болатын құрылымдық тип операциясына негізделген. Бұл модельдің жақтаудағы жол үсті монипуляция типтері нақты түоде шектелмеген. Грамматика деп а. Екінші моделінде бізді қызықтыратын жолдармен берілген монипуляциялар ғана емес, берілген алфавиттен алынған анықталған қатар жиындарының туындылары. Екі модельде тәжіриберлік бағалануды көрсетеді не осы бөлінің келесі параграфтарында көрсетілген мысалдармен дәлелденге. Біз зерттеп отырған жолдарды манипуляциядардың алғашқы формальдау жүйесі кәдімгі Марков алгоритмі береді. Ол формальді математикалық жүйе бола тұрып, жолдарды қайта құрудың бірінші тілі СОМІТ-тің негізінің қолданылатын СНОБОЛ программалау тілі арасында таң қаларлық ұқсастық бар.

Алгоритм ұғымын формальдау үшін орыс математигі А. А. Марков ассоциативтік есептеулерді қолдануды 1953 жылы ұсынды. Мұнда алгоритм ауыстырымдар жүйесі түрінде беріледі. Олар қандай символдарды ауыстыру керек екендігін және бұл ауыстырулар қандай ретпен жүретіндігін көрсетеді. Мұндай тәсілді А. А. Марков елуінші жылдары ұсынды, ол нормальды алгоритм ұғымын енгізді.

Қарапайым (Марковтік) өнім деп u→w түріндегі жазбаны айтады, мұндағы u және w-V’ жолдары, себебі V алфавиті құрамына «→» жане «. » символдары кірмейді.

А. А. Марков ұсынған алгоритм ұғымын анықтау тәсілі мына төмендегідей анықталатын қалыпты алгоритм ұғымына негізделген. А әріппесі және В алмастырулар жүйесі берілсін. Кез келген Р сөзі үшін В-дағы алмастырулар сол В-дағы өз ретімен алынады. Егер келісті алмастыру табылмаса, үрдіс тоқтатылады. Керісінше жағдайда келісімді алмастырулардың біріншісі алынып, оның Р-дағы солжақ бөлігінің бірінші кірісі оның оңжақ бөлігімен ауыстырылады. Сонаң соң барлық әрекет жаңадан алынған Р1 үшін қайталанады. Егер В жүйесінің соңғы алмастыруы қолданылатын болса, үрдіс тоқтатылады. Мұндай ұйғарымдар жиыны А әріппесімен және В алмастырулар жиынымен қалыпты алгоритмді анықтайды. Үрдіс екі жағдайда ғана тоқтайды: 1) тиімді алмастыру табылмаған жағдайда; 2) олардың жиынындағы соңғы алмастыру пайдалынылған жағдайда. Әртүрлі қалыпты алгоритмдер бір-бірінен әріппелері және алмастырулар жүйесі арқылы ерекшеленеді. Натурал сандарды (бірлер жиынымен берілген) қосуды сипаттайтын қалыпты алгоритмге мысал келтірейік.

Мысал : Әріппе Алмастырулар жүйесі

P сөзі: 11+11=111

Р сөзін Марковтың қалыпты алгоритмі арқылы біртіндеп қайта өңдеу мына кезеңдер арқылы өтеді:

Марковтың қалыпты алгоритмін кез келген алгоритм берілуінің әмбебап түрі ретінде қарастыруға болады. Қалыпты алгоритмдер әмбебаптығы қалыптастыру принципі арқылы жарияланады: кез келген ақырлы А әріппесінде кез келген алгоритм үшін оған пара-пар А әріппесі бойынша қалыпты алгоритм құруға болады. Соңғы тұжырымды түсіндірейік. Кейбір жағдайларда алмастыруларында тек А әріппесінің әріптерін пайдаланатын болсақ, А әріппесінде берілген алгоритмге эквивалент қалыпты алгоритм құрылмайды. Дегенмен, А әріппесін кеңейту арқылы (оған жаңа әріптерді қосу арқылы) қажетті, қалыпты алгоритм құруға болады. Бұл жағдайда, бастапқы А әріппесіндегі сөздерге ғана қолданылатын болса да құрылған алгоритмді А әріппесі бойынша алгоритм дейді. Егер N алгоритмі А әріппесінің кейбір кеңейімінде берілген болса, онда N А әріппесі бойынша қалыпты алгоритм дейді.

Р=11+11+111 P5=+1+

P1=1+11+111 Р6=++

P2=++111 P7=+

P3= +111+ Р8=

P4=+11+ P9=

Машинаның Құрылымы

Тьюринг машинасы 3 бөліктен тұрады: лентадан, оқитын-жазатын бөлшектен және логикалық құрылғыдан.

Лента сыртқы жады қызметін атқарады; ол шексіз деп есептеледі - мұның өзі Тьюринг машинасы модельді құрылғы екенін көрсетеді, өйткені ешбір құрылғы шексіз өлшемді жадыдан тұрмайды. Лента жеке ұяшықтарға бөлінген, оған (0, 1, …, N-1) алфавитінің символдары жазылады. Тьюринг машинасында бөлшек қозғалмайды, ал лента оған қатыстыоңға не солға қозғалады. Екінші бір ерекшелігі ол екілік емес қандайда да бір шектелген алфавитінде-сыртқы алфавитте жұмыс істейді. Онда арнайы символ -бос таңба болады. Оны қандайда да бір ұяшыққа орналастырса, ондағы таңбаны өшіреді жіне ұяшықты бос етеді. Лентаның әрбір ұяшығына тек бір символ жазылуы мүмкін. Лентада сақталаты ақпарат сыртқы алфавиттің бос таңбадан өзгеше таңбалардың шектелген тізбегімен кескінделеді. Автомат(q1, . ., qr) күйінің бірінде бола алады және әр уақыт аралығында (R, L, S) қозғалысының біреуін жүзеге асырады:R-бір ұяшыққаоңға орын ауыстыру, L-бір ұяшыққа солға орын ауыстыру, S-орнында қалу. Мұндай құрылғының жұмысын баңдарлама деп аталатын арнайы кесте көмегімен беруге болады. Сол жақ шеткі бағанда (0, 1, …, N-1) (машинаның сыртқы алфавиті) алфавитінің символдары орналасады. (q1, . ., qr) жиыны-машинаның ішкі алфавиті. Бұл кестенің кейбір торларыбос болуы мүмкін. Бұл кесетнің торларына

cDq

N-1

∆

z1S

z∆S

q1R

z1S

Ішкі алфавит Q=(q, z) жиынымен беріледі, мұндағы q- логикалық құрылғының жұмыс күйіне, ал z-тоқтатуға сәйкес келеді. Барлық түрлендірулер ережесінің жиынтығы төмендегі функ-дық схема түрінде көрсетілуі мүмкін.

Баған және жолдарын білдіретін танбалар логикалық құрылғынын ішкі параметрлерін аныктайтындай, ал олардың қиылысуындағы ұяшықта сырткы команда тұратын функ-дық схема кесте түрінде құырлады. Дербес жагдайда егер машинаның бастиегі лентаның 1 танбасы бар секциясын бақыласа және машина (q) жұмыс күйінде болса, онда онын берілген тактідегі жұмыс нәтижесі берілген секцияда бірді қайталау және бір секцияға оңға өту болып табылады-бұл команда былай жазылады q1R. Егер бақыланатын секцияда ∆ болса, онда ∆ 1-ге ауыстырылады, лентанын ығысуы болмайды және машина токтайды - z1S.

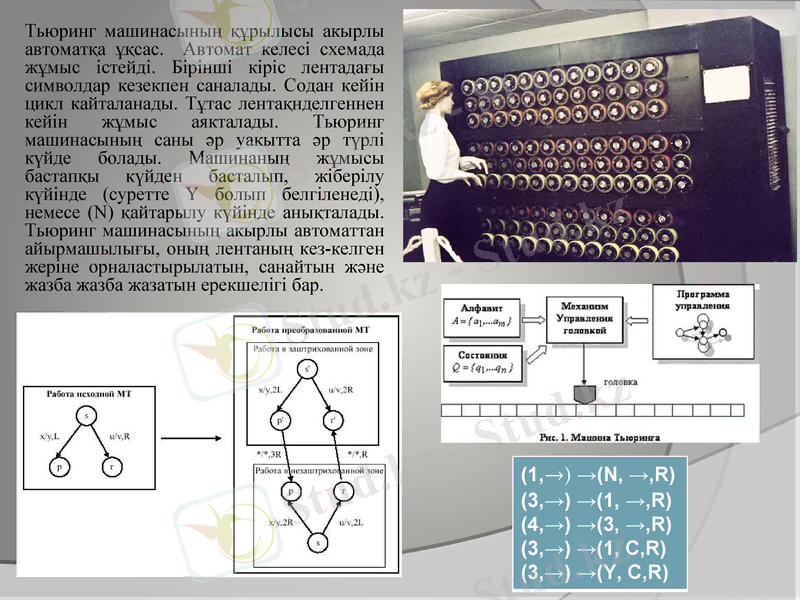
Тьюринг машинасының құрылысы акырлы автоматқа ұқсас. Автомат келесі схемада жұмыс істейді. Бірінші кіріс лентадағы символдар кезекпен саналады. Содан кейін цикл кайталанады. Тұтас лентақнделгеннен кейін жұмыс аякталады. Тьюринг машинасының саны әр уакытта әр түрлі күйде болады. Машинаның жұмысы бастапқы күйден басталып, жіберілу күйінде (суретте Ү болып белгіленеді), немесе (N) қайтарылу күйінде анықталады. Тьюринг машинасының акырлы автоматтан айырмашылығы, оның лентаның кез-келген жеріне орналастырылатын, санайтын және жазба жазба жазатын ерекшелігі бар.

Машинаның құрылымына кіреді

а) шексіз таспа (ұяшықтарға бөлінген) . Әрбір ұяшыққа тек бір ғана әріп жазылуы мүмкін.

б) оқып - жазушы құрылғы. Оқып - жазушы құрылғының шолу жасау, ұяшыққа жазылған әріпті оқу, ұяшыққа әріпті жазу, жылжу мүмкіндіктері бар.

в) басқару құрылғысы - машинаның программасы көмегімен машина жұмысын басқарады.

г) машинаның бір конфигурациясынан басқасына өтулерін анықтайтын машинаның программасы. Егер шолу жасалған ұяшық пен машинаның жағдайы белгілі болса, онда машинаның конфигурациясы белгілі деп аталады.

Тьюринг машинасының 3 алфавиті бар:

1. Бос символмен берілген сыртқы алфавит -А É {L}.

2. Ішкі алфавит немесе жағдайлар алфавиті Q={q₀, q₁, …., qn }. q₀ жағдайы қорытынды жағдай, q₁-бастапқы жағдай, q₂, q₃, …. qn - жұмыс жағдайлар деп аталады.

3. Қозғалыстар алфавиті S={-1, 0, +1}.

Чёрча-Тью́рингтің Те́зисі

Бұл тезис математикалық теорема болып есептелінбейді. Ол дәллелдене алмайды, тек кана дұрыс болуы мүмкін. Чёрча-Тью́рингтің Те́зисі - информатика, кибернетика, т. б. ғылыми облыстарда фундаментальдық бекіткен. Бұл тезисті Алонзо Чёрча пен Аланом Тьюринг 1930-жылдардың ортасында ұсынды. Олардың айтуынша. Алгоритмдерді жүзеге асыратын барлық механизмдер, негізінен бір-біріне ұқсас болып келеді. Тезистің тұжырымдауынша, программаға колданатын белгілі бір әдіс мүлдем жоқ. Бұл бір жа, ынан шындық сиякты. Мысалы, егер сізге екі санды көбейтіңіз деп сұраса, онда сіз мүмкін қарапайым алгоритмді қолдануыныз мүмкін, ол программаланған болады. Ал егер осы сандарды көбейткіштерге жіктеуді сұраса, онда сіз оған арнайы әдісті қолданасыз, ол әрине прграммамен жазылған болушы еді.

Ұқсас жұмыстар

Тьюринг машинасы. Тьюринг тезисі және оның негіздемесі

Тьюринг машинасы. Тьюринг тезисі жә не оның негіздемесі. Марковтың нормальды алгоритмы. Нормальдау принциптері жә не оның негіздемесі. Марковтың нормальды алгоритмі жә не Тьюринг машинасының композициясы

Тьюринг тезисі және оның негіздемесі

Тьюринг машинасы. Тьюринг тезисі және оның негіздемесі. Марковтың нормальды алгоритмы. Нормальдау принциптері және оның негіздемесі. Марковтың нормальды алгоритмі және Тьюринг машинасының композициясы

Марковтың нормальды алгоритмі

Тьюринг тезисі және оның негіздемесі. Марковтың нормальды алгоритмы. Нормальдау принциптері және оның негіздемесі. Марковтың нормальды алгоритмі және Тьюринг машинасының композициясы

Тьюринг машинасы. Алан Мэтисон Тьюринг

Программалау тілдері туралы ақпарат

Тьюринг машинасы және Пост машинасы

Тьюринг машинасы

Пәндер