Алгоритмдер туралы түсінік

Презентация қосу

Алгоритмдер туралы
түсінік
Жоспар:

Кіріспе
Алгоритм туралы жалпы түсінік
Негізгі бөлім
2.1 Есептеу процесі ұғымы.
2.2Алгоритм күрделілігі. Aлгоритмнің уақытша
күрделілігі. Aлгоритмнің теориялық күрделілігі.
2.3 есептелетін функция ұғымы. Рекурсия ұғымы,
рекурсивті функция. Компьютер көмегімен есептелетін
функциялар теориясы.
Қорытынды
Пайдаланылған әдебиеттер
Алгоритм - информатика пәнінің негізгі ұғымдарының
бірі.Компьютерді қоғам өмірінің қай саласында болмасын
пайдалана білу үшін алгоритм ұғымын меңгеру керек.

«Алгоритм» сөзі мағынасы жағынан нұсқау, жарлық,
рецепт, ереже, тәртіп, заң, жоба сөздеріне синоним болып
келеді. Алгоритм сөзі Орта Азияның ортағасырлық ұлы
ғалымы - Мұхамед ибн Мұса әл-Хорезмидің атымен
байланысты шыққан. Ол өзінің «Арифметикалық трактат»
деген еңбегінде
арифметикалық амалдарды орындау тәртібін ұсынған.
Алгоритмдік процесс дегеніміз – шешілетін
есептің нақты бастапқы берілгендеріне
алгоритмді қолдану процесі.
Алгоритмді ұсыну құралдары:
• ауызша (алгоритмдік тілде);
• блок-схема түрінде;
• бағдарламалау тілінде.

Алгоритмдеу – ЭЕМ-де есепті шығаруға
арналған алгоритмдер мен бағдарламаларды құру
техникасы.

Алгоритмнің блок-схемасы дегеніміз –
алгоритмнің логикалық құрылымын графикалық
бейнелеу.
БЛОКТАР
Басын және соңын
білдіретін тоқтату блогы
Берілгендерді енгізіп,
нәтижелерді шығаратын
енгізу-шығару блогы
Арифметикалық
амалдарды орындайтын
процесс блогы
Шарттың орындалу
немесе орындалмауын
тексеретін шешім
қабылдау блогы
Қайталану блогы
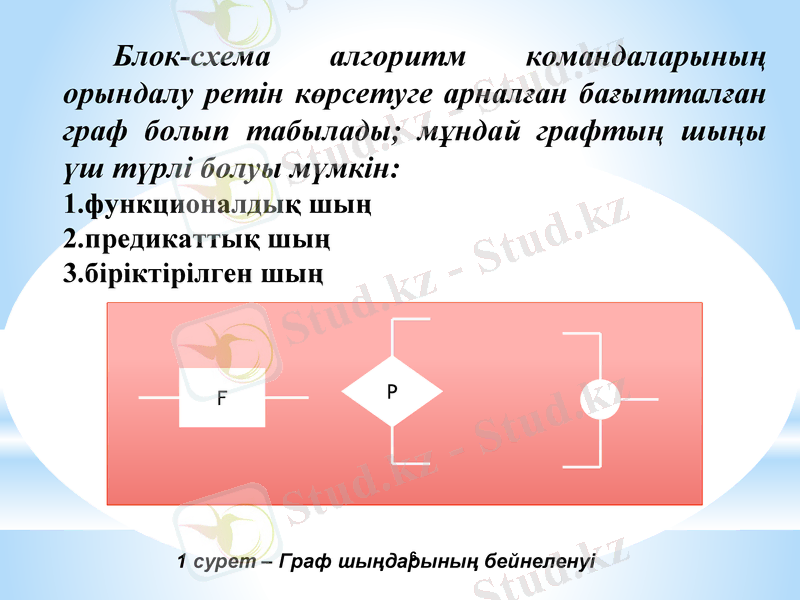
Блок-схема алгоритм командаларының
орындалу ретін көрсетуге арналған
бағытталған граф болып табылады; мұндай
графтың шыңы үш түрлі болуы мүмкін:
1.функционалдық шың
2.предикаттық шың
3.біріктірілген шың

F P

1 сурет – Граф шы ңдарының бейнеленуі
Алгоритмнің қасиеттері

Дискреттік қасиеті. Алгоритмдік үрдіс жеке
қадамдарға бөлінуі қажет. Әрбір келесі бұйрықты
орындау үшін алдыңғы бұйрықты орындау қажет.

Түсініктілік қасиеті. Тәжірибе жүзінде
қолданылатын алгоритмдер белгілі бір орындаушыға
арналады, сондықтан ол алгоритмді құру үшін
орындаушыға түсінікті болуы керек, яғни
орьшдаушының бүйрықтар жүйесін білу қажет.
Анықтық немесе детерминдік қасиеті. Алгоритм
түсінікті болуымен қатар мағынасы әр түрлі
бұйрықтардан тұрмауы қажет, яғни алгоритм
орындаушының еркіндігіне жол бермеуі қажет.

Нәтижелілік қасиеті. Кез келген алгоритм
қадамдарының саны шектеулі болу керек және белгілі бір
нәтижеге жетуі қажет. Есептің шешімі жоқтығы да
нәтиже болып есептеледі.
Көпшілік қасиеті немесе жалпылылығы.
Көптеген алгоритмдер тек қана бір есепті ғана
емес, бір типті есептер кластарының шешімін
табуға мүмкіндік береді. Қарапайым жағдайда
көпшілік қасиеті алгоритмді әр түрлі алғашкы
мәліметтер үшін қолдануға мүмкіндік береді.
Бір есепті шешу үшін тек жалғыз алгоритм емес бірнеше алгоритм
құруға болатыны белгілі. Сондықтан есепті шешу үшін барлы қ
алгоритмдердің ішінен ең тиімдісін құру қажет болады. Алгоритмді
орындаушы-адам болған жағдайда алгоритмнің күрделігі логикамен
байланысты, себебі, есепке құрылған алгоритмнің ішінде к үрделі
структура болса, одан қандай нәтиже алынатынын алдын ала болжау
мүмкін емес, тек оны орындап болған соң нәтижені ң д ұрысты ғы,
бұрыстығы зерттеледі, ал орындаушы-машина болса, оған алгоритмні ң
структурасы қаншалықты күрделі екендігі әсер етпейді, себебі машина
үшін белгілі нұсқаулар берілді, ол соны орындайды, мысалы: машина ға
бәрібір – қосуды орындап жатыр ма азайтуды орындап жатыр ма, әйтеуір
техникалық жабдығы дұрыс болса, алдына қойған проблема шешіледі.
Немесе алгоритмді жазғанда қайталану операторын қолданбай а қ к үрделі
есепті шешудің өте көп қадамнан тұратын тізбекті структурасын
қолдануға болады, ал машинаға бәрібір- циклды қолдандың ба, тізбекті
қолдандың ба, бірақ есептеу уақыты, алынған нәтиже адамды
қанағаттандырмауы мүмкін, сондықтан алгоритмнің күрделілігі деген
ұғым қажеттілігі шығады.
Анықтама. Алгоритмнен туындаған есептеу процесі деп осы
алгоритмді орындау барысында өткен тізбекті қадамдар алгоритмін
айтады.
Анықтама. Алгоритмнің күрделілігі – осы алгоритмді есептеу
процесінде қолданылған элементарлы қадамдар саны.
Анықтама. Алгоритмнің уақытша күрделілігі – оны орындауға
қажетті Т уақыты. Ол элементарлы әрекеттер саны мен оны
орындауға кеткен орташа уақыттың көбейтіндісіне тең:T=kt.
t- уақыт орындаушы – машинадан тәуелді болса, алгоритмні ң
күрделілігі k-элементарлы әрекеттер тізбегінің санынан тәуелді.
А алгоритмі бар болсын. Оған деректерді өңдеу көлемін
көрсететін а параметрі табылсын. Оны (а) - есептің өлшемі дейді.
Т арқылы алгоритмнің орындалу уақытын белгілесе, / -ар қылы
әлдебір n-нан тәуелді функцияны белгілейік.
Анықтама. T(n) алгоритмінің өсу реті f(n) бар,
немесе басқаша, алгоритмнің теориялық күрделілігі
O*(f(n)) бар болады, егер c1, c2>0 тұрақтылары және
барлық n<=n0 үшін
c1 f(n)табылса. Мұндағы f(n) функциясы ең болмағанда n<=n0
үшін теріс емес болуы керек. Егер T(n) үшін T(n)<=cf(n)
шарты орындалса, онда алгоритмнің теориялық
күрделілігі O(n) болады. (n-нен үлкен «0» деп оқылады.).
Шама дегеніміз есепті шығару барысында
қолданылатын белгілеулер. Олар 3 топқа
бөлінеді:
1. аргументтер – енетін шамалар
2. аралық шамалар
3. нәтижелер – шығатын шамалар
Алгоритмнің қызметі – берілген информацияны өңдеу арқылы
басқа, жаңа информацияны құру.
Берілген информацияны алғашқы информация дейді.
Алгоритм үшін бастапқы берілгендер немесе алғашқы информация
болып табылатын шамаларды енетін шамалар немесе аргументтер деп
атайды.
Алгоритмнің орындалу процесінде алынатын өңделген
информацияларды сақтауға арналған шамаларды шығатын шамалар
деп атайды.
Енетін шамаларға да, шығатын шамаларға дажатпайтын алгоритмді
орындау процесінде аралық мәндерді сақтауға арналған шамаларда
аралық шамалар дейді.
Шамалар 2 бөліктен тұрады:
1. шаманың аты – белгіленуі өзгермейді
2. шаманың мәні – өзгеріп отырады
Шама жәшік сияқты, жәшіктің сырты белгіленеді – ол аты, ішіне зат
салумен беру сияқты болады.
Шамалар программасындағы қызметіне қарай:
1. тұрақты шамалар
2. айнымалы шамалар
Мәні алгоритмді орындау барысында өзгермейтін, алгоритм тексінде
көрсетілген қалпында қала беретін шамаларды тұрақты шамалар дейді.
Алгоритмді орындау процесінде мәндері өзгеріп отыратын
шамаларды айнымалы шамалар дейді.
Шамалар алгоритмде қызметіне қарай бірнеше болып бөлінеді:
3. натурал
4. бүтін
5. нақты
6. литерлік
Анықтама. Әлдебір алгоритм көмегімен есептелетін функцияны
есептелетін функция дейді.
Іс жүзінде алгоритм – функцияны беру әдісі. Ал функция таблица,
схема, формула түрінде берілуі мүмкін. Бірақ кейбір процестерде
бастапқы енгізілген немесе берілген деректер мен алынған нәтижедегі
деректер арасындағы байланысты ұйымдастыратын функцияны құру
қиын, күрделі.
1 – бағыт Рекурсивті функциялар – есептелетін функциялар ұғымымен
байланысты.
X және Y жиындары бар болсын. X жиынының кейбір
элементтеріне Y жиынының элементтері сәйкес келсе, онда Y – те X –
тен бөлшекті функция берілген дейді.
Y жиынында сәйкес элементтері бар және X элементтерден
құралған жиынның элементтер жиыны функцияның анықталу
облысы деп аталады.
X жиынында сәйкес элеметтері бар Y жиынының элементтер жиыны
функцияның мәндер облысы деп аталады.
Егер X –тен Y-тегі функцияның анықталу облысы X жиынымен
беттессе, онда ол функцияны барынша анықталған деп атайды.
Осы ұғымға және рекурсивті функцияға негізделіп алгоритмнің
дәл анықтамасын құруға болады.
Кез – келген берілген деректерді (үзілісті, дискретті) әлдебір санау
жүйесінде натурал сандармен кодтауға болады, онда оларды ң барлы қ
алмастыруы есептеу операцияларының тізбегіне келтіріледі, ал өңдеу
нәтижесі солайынша бүтін сан болып қалады. Кез келген алгоритм
берілген сандық функция үшін бірдей, оның мәнін есептейді, ал оны ң
элементарлы қадамдары қарапайым арифметикалық және логикалы қ
операциялар болады. Мұндай функциялар есептелетін функциялар
деп аталады.
Y(x ,,,, x ) функция класы бар болсын. Аргументтер бүтін, нәтижеде
бүтін сан немесе аргументі де нәтижесі де дискретті болсын.
Y(x ,,,, x ) функциясы тимді есептелетін функция деп аталады, егер
белгілі аргументтер мәндері бойынша оның мәнін есептейтін алгоритм
бар болса.
Әр түрлі түсінілетін процесстер үшін есептелетін функциялар тізімі
(алгоритмнің барлық қасиеттерін қанағаттандыратын) кәдімгі
математикалық терминмен жеңіл сипатталатын функциялар болса,
рекурсивті деп аталады.
Бөлшекті функцияның суперпозициясы

m – орынды f функциялар n – орынды g (x ,,,, x )
функциясына қойылатын болсын. Нәтижеснде n –
орынды функциясы алынады.
Мұны h функциясы g функциясынан суперпозиция
арқылы алынды деп айтады.
Мұндай қою - деп берілгенді n- функция саны, олар
келесі бір функцияның g-дің аргументтері ретінде
қойылып тұр.
Егер функциялары есептелетін болса, n- функциясы да
есептеледі. Онда функциялары интуитивті есептелетін
болса, n- функциясы да интуитивті есептеледі.
Назарларыңызға
рахмет!!!
Пайдаланылған әдебиеттер:

1.Https://ru.wikipedia.org/wiki/Алгоритм
2 .Б.Д.Сыдықов “Алгоритм теориясы” Алматы 2012ж.
3.Htt://studopida.net/10_104972_cherch—tyuring-tezis
4.Htt://kinostan.kz/news/view?id=443

Ұқсас жұмыстар

Алгоритмдер туралы түсінік. Алгоритм күрделілігі

Бастауыш мектепте компьютерлік технологияны қолданудың қазіргі жағдайы

Алгоритм күрделілігі

Алгоритм түсінігі

Шешілмейтін алгоритмдер туралы тү сінік. Алгоритм кү рделілігі. Алгоритм тү сінігінің функция тү сінігімен байланысы. Алгоритмдік тіл жә не оны орындаушылардың сипаттамалары

Алгоритмдер ұғымы туралы түсінік

ЕСЕПТЕУДІҢ АЛГОРИТМДІК ШЕШІМІ АЛГОРИТМДІК КҮРДЕЛІКТІ ТАЛДАУ

Криптографияның математикалық негіздері

Алгоритм туралы мәлімет

Шешілмейтін алгоритмдер туралы түсінік

Пәндер