Ықтималдықтар теориясының негізгі түсініктері. Ықтималдық теориясын көбейту теоремасы

Презентация қосу

ЫҚТИМАЛДЫҚТАР
ТЕОРИЯСЫНЫҢ НЕГІЗГІ
ТҮСІНІКТЕРІ.
ЫҚТИМАЛДЫҚ
ТЕОРИЯСЫН КӨБЕЙТУ
ТЕОРЕМАСЫ.
Ықтималдық теориясы
Ықтималдық теориясының негізгі мақсаты – біртекті
кездейсоқ оқиғалардың жалпы ықтималдық
заңдылықтарын зерттеу болып табылады.
Оқиғалар: ақиқатты, мүмкін емес және кездейсоқ
болып бөлінеді.
Кездейсоқ оқиғалар дегеніміз кейбір жағдайларға
байланысты сынау кезінде оқиғалардың пайда болуы
не болмау мүмкін оқиғаларды айтамыз.
Кездейсоқ оқиғалар: үйлесімсіз, бір ғана
мүмкіндікті, тең-мүмкіндікті болып бөлінеді. Оқиғалар
үйлесімсіз деп аталады, егер бір сонау кезінде
оқиғаның пайда болуы оқиғалар бір-бірін шығару
орын алатын болса.
Пайда болу тарихы
Ықтималдылық теориясы 17 ғ-дың орта кезінде пайда болды. Ықтималдылық
теориясы 17 ғ-дың орта шенінде әйгілі ғалымдар Б.Паскаль (1623 – 62) мен
П.Ферма (1601 – 65), Х.Гюйгенс (1629 – 95), Я.Бернулли (1654 – 1705), Муавр (1667
– 1754), Гаус (1777 – 1885) еңбектерінде пайда болып, әрі қарай дамыған. Қазір
Лаплас (1812) пен Пуассон (1837) теоремаларының дәлелденуі осы кезеңге
жатады; ал А.Лежандр (Франция, 1806) мен К.Гаусс (1808) ең кіші квадраттар
тәсілін жетілдірді. Ықтималдылық теориясы тарихының үшінші кезеңі (19 ғ-дың 2-
жартысы) негізінен орыс математиктері П.Л. Чебышев, А.М. Ляпунов және А.А.
Марков (үлкені) есімдеріне байланысты. 19 ғ-дың 2-жартысында Батыс Еуропада
матем. статистика (Белгияда А.Кетле, Англияда Ф.Гальтон) мен статис. физика
(Австрияда Л.Больцман) бойынша көптеген еңбектер жазылды. Бұл еңбектер
(Чебышев, Ляпунов және Марковтардың негізгі теор. еңбектерімен қатар)
ықтималдылық теориясы тарихының төртінші кезеңінде ықтималдылық
теориясының шешілуге тиісті мәселелерінің аясын кеңейтті. Бұл кезеңде шет
елде де (Францияда Э.Борель, П.Леви, т.б., Германияда Р.Мизес, АҚШ-та Н. Винер,
т.б., Швецияда Г.Крамер) КСРО-да өте маңызды зерттеулер жүргізілді.
Ықтималдылық теориясының жаңа кезеңі С.Н. Бернштейннің зерттеулерімен
байланысты. Ресейде А.Я. Хинчин мен А.Н. Колмогоров ықтималдылық
теориясының мәселелеріне нақты айнымалы функциялар теориясының тәсілдерін
қолдана бастады. Кейінірек (30-жылдары) олар процестер теориясының негізін
қалады. Қазақстан ғалымдары да (І.Б. Бектаев, Б.С. Жаңбырбаев) Ықтималдылық
теориясы бойынша зерттеулер жүргізіп келеді.
Мысал : ойын тасын (біртекті куб) тастағанда,
ол алты жағына түсуі мүмкін. Егер оларды 1, 2,
3, 4, 5, 6 деп белгілесек, 7 түсуі жалған, осы
алты жағының бірі түсуі айқын оқиғалар.

Ал жұп ұпайдың түсуі, түспеуі кездейсоқ оқиға,
өйткені оның яғни 2, 4, 6 жағының түсуін
алдын-ала болжай алмаймыз. Ол нәтижеге
байланысты. Нәтиже дегеніміз, кездейсоқ
тәжірибені аяқтайтын және бір-бірін өзара
жоққа шығаратын нұсқалардың бірі.
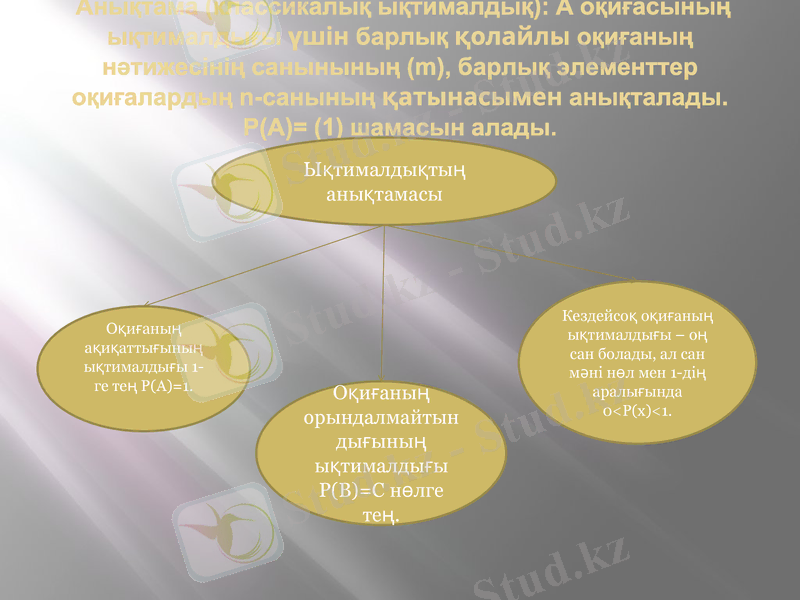
Анықтама (классикалық ықтималдық): А оқиғасының
ықтималдығы үшін барлық қолайлы оқиғаның нәтижесінің
санынының (m), барлық элементтер оқиғалардың n-санының
қатынасымен анықталады. Р(А)= (1) шамасын алады.

Ықтималдықтың
анықтамасы

Кездейсоқ
Оқиғаның
оқиғаның
ақиқаттығының
ықтималдығы –
ықтималдығы
оң сан болады, ал
1-ге тең Р(А)=1.
сан мәні нөл мен
Оқиғаның 1-дің аралығында
орындалмайты 0<Р(х)<1.
ндығының
ықтималдығы
Р(В)=С нөлге
тең.
Ықтималдықтарды көбейту
теоремасы
Екі А және В оқиғалардың бір кезде орындалуы деп олардың
ықтималдықтарының көбейтіндісіне айтылады. Егер А оқиғаның
орындалу ықтималдығы басқа бір оқиғаның орындалуына
байланысты болмаса А оқиғаның орындалу ықтималдығына
шарттсыз ықтималдық делінеді. Мысалы екі ойын сүйегін
тастағанда бірінші ойын сүйегінде 5 тік ұпайының түсуі екінші
ойын сүйегінде қандай ұпайдың түсуіне байланысты емес.
1-теорема. Бір-бірінен байланысты емес оқиғалардың
ықтималдықтарын көбейту: бір-біріне байланыссыз оқиғалардың
екеуінің немесе бірнешеуінің бірдей пайда болуының
ықтималдығы: Р(және А, және В)=Р(А)•Р(В), Р(и А1, и А2,…и
АП)=Р(А1)•Р(А2)•Р(АП).
2 теорема. Бір-біріне байланысты оқиғалардың ықтималдықтарын
көбейту: бір-біріне байланысты оқиғалардың біреуі немесе
бірнешеуі орындалдының ықтималдығы біреуінің ықтималдығын
бірінші оқиға орындалуы деп Рв(А) екіншісінің ықтималдығының
көбейтіндісіне тең, яғни Р (и А1 и В)=Р(А)•Ра(В), Р(и А1, и А2, …и
Ап)=Р(А1)•Ра1(А2)•… •Р а1…п-1 (Ап).
Мысал
Мысал. М О С К В А сөзін құрастыратын кеспе
әріптер әбден араластырылып, 4 кеспе әріпті
қатарынан қойғанда К В А С сөзінің шығу
ықтималдығын анықтау керек.
Шешуі: Бірінші алынған кеспе әріп К болуы А1
оқиғасы болсын, екіншісі В болуы –А2, үшіншісі А
болуы –А3, төртіншісі С болуы А4 оқиғасы болсын
десек, онда КВАС сөзінің пайда болуы А оқиғасы
болады. Көбейту теоремасы бойынша
Р(А)=Р(А1А2А3А4 )=Р(А1)*Р(А2)*Ра1а2(А3)*Ра1а2а3(А

4)=
1 1 1 1 1
6*5*4*3 360
болып шығады.

Ұқсас жұмыстар

ЫҚТИМАЛДАР ТЕОРИЯСЫ

Ықтималдық теориясының басты түсініктері және теоремасы. Моменттер. Дисперсия. Орташа квадраттық ауытқулар

Кездейсоқ оқиғаны модельдеу

Ықтималдықтар теориясының даму тарихы

Ықтималдықтар теориясы. Негізгі түсініктері. Кездейсоқ шаманың сандық сипаттамасы. Математикалық күтім

Ықтималдық теориясы

Ықтималдықтың классикалық анықтамасы

Оқиға бірнеше түрге бөлінеді сенімді

Ықтималдылық алгоритмінің сапа көрсеткіштері

Оқиғаның ықтималдығы және оның қасиеттері

Пәндер