Сызықтық теңдеулер жүйелері және олардың классификациясы: матрицалық жазылуы және Крамер ережесі

Сызықтық теңдеулер жүйесі және оның классификациясы

Сызықтық теңдеулер жүйесін крамер формуласымен шешу

түріндегі теңдеулер жүйесін сызықтық

теңдеулер жүйесі деп атайды. Осындай

m теңдеудің жүйесі қысқаша былай жазылады:

Анықтама: Егер

теңдігі орындалса

сандарының жиыны (1) теңдеулер жүйесінің шешімі деп аталады.

Егер сызықтық теңдеулер жүйесінің ең болмағанда бір шешімі бар болса, онда ол үйлесімді деп, ал егер шешімі болмаса үйлесімсіз деп аталады.

(1) сызықтық теңдеулер жүйесімен қатар

теңдеулер жүйесін қарастырайық.

Анықтама: Егер (1) теңдеулер жүйесінің әрбір шешімі (2) теңдеулер жүйесінің шешімі болса, онда (2) теңдеулер жүйесін (1) теңдеулер жүйесінің салдары деп атайды.

Егер (1) теңдеулер жүйесінің барлық шешімінің жиыны (2) теңдеулер жүйесінің шешімдер жиынының ішкі жиыны болса, сонда тек сонда, (2) сызықтық теңдеулер жүйесі (1) - нің салдары болады.

Анықтама: Егер сызықтық теңдеулер жүйесінің біреуінің әрбір шешімі екінші жүйенің шешімі де болса, онда бұл теңдеулер жүйелері тең мағыналы деп аталады.

Егер сызықтық теңдеулердің екі жүйесінің әр біреуі екіншісінің салдары болса, онда бұл теңдеулер жүйелері тең мағыналы болады. Сонымен қатар сызықтық теңдеулердің екі жүйесінің біреуінің шешімдер жиынын екіншісінің барлық шешімдер жиынымен беттессе, онда осы екі жүйе тең мағыналы болады.

Берілген n белгісізді m теңдеулер жүйесін матрицалық түрде былай жазуға болады: A∙X=B

Мұндағы А жүйенің коэффициенттерінен құралған матрица, оны жүйенің негізгі матрицасы деп атайды.

Негізгі матрицаға бос мүшені тіркеп жазғаннан шыққан матрица жүйенің кеңейтілген матрицасы деп аталады.

n белгісізді n теңдеулер жүйесі берілсін

Бұл жүйенің негізгі матрицасы квадраттық матрица. Оның анықтауышы жүйенің анықтауышы деп аталады.

Сызықтық теңдеулер жүйесін крамер формуласымен шешу

Егер болса, жүйе туындамаған деп аталады.

болған жағдайда жүйені шешейік. Берілген жүйені матрицалық түрде жазып алайық.

A∙X=B. Бұл теңдеудің екі жағын да сол жақтан

көбейтіп

Сызықтық теңдеулер жүйесінің бұл шешуі матрицалық әдіспен шешу деп аталады. Бұл шешімді матрицалық түрде былай жазамыз.

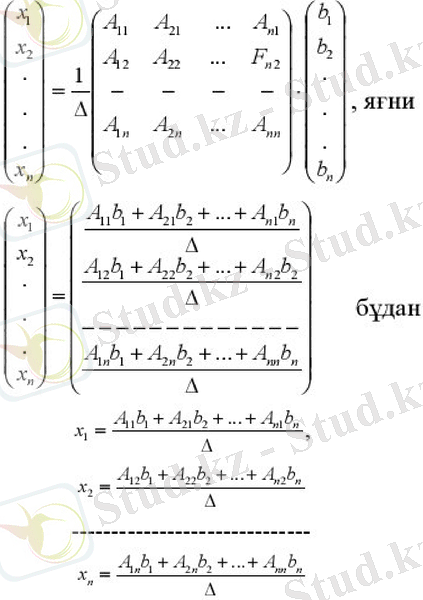
анықтауышының бірінші бағанның элементтері бойынша жіктелуі болып табылады. анықтауышы анықтауышының бірінші бағанын бос мүшелерден құрылған бағанмен ауыстырудан алынған.