Марковтың нормальды алгоритмі

Презентация қосу

Қазақстан Республикасының Білім және ғылым министрлігі
Семей қаласының Шәкәрім атындағы Мемлекеттік университеті
Жаратылыстану – математика ғылымдар факультеті

СӨЖ №1

Орындаған: Бекбосунова Мариям Т- 311

Тексерген: Рысжанова Айжан Сайлаухановна

Семей 2015 жыл
Жоспар:
1. Тьюринг машинасы. Тьюринг
тезисі және оның негіздемесі.
2. Марковтың нормальды алгоритмі.
3. Нормальдау принциптері және
оның негіздемесі.
4. Тьюринг машинасының
композициясы.
• Информатиканың негізгі ұғымдарының бірі болып
алгоритм ұғымы саналады.
• Алгоритмдер – математика және информатиканың
шекарасындағы математикалық логикаға жанасатын –
алгоритмдер теориясы деп аталатын ғылыми пәннің
жүйесі зерттеулерінің объектісі болып саналады.
• 1936 жылы ағылшын математигі Алан Тьюринг
алгоритмді нормальді түрде анықтауға мүмкіндік
беретін, кейінірек тьюринг машинасы деп аталған
абстрактілі есептеуіш конструкциясын ұсынды. Бұл
машина толық детерминделген әмбебап орындаушы
болып табылады. Ол алғашқы деректерді «енгізіп» және
бағдарлама орындалғаннан кейін нәтижені «оқуға»
мүмкіндік береді.
Алан Тьюринг
Алан Мэтисон Тьюринг (23.06.1912 -
07.06.1954) — информатиканың
дамуына үлкен үлес қосқан ағылшын
математигі, логигі, криптографы. Ұлы
Отан соғысы кезінде Алан Тьюринг
Блетчли-паркта орналасқан Үкіметтік
Байланыс Орталығында қызмет
атқарды.Тьюринг Жапония, Германия
және Италия секілді нацисттік елдер
мен олардың жақтаушыларың құпия
жазбаларын, шартты белгілерінің
мағынасын ашумен айналысқан. Ол
Германияның әскери-теңіз флотының
хабарламаларының криптоанализіне
жауапты Hut 8 тобын басқарды.
Тьюринг криптоанализдің бірқатар
тәсілдерін ойлап тапты. Соның ішінде,
неміс шифраторы Enigma-ның құпия
жазбаларын шешуді мақсат ететін
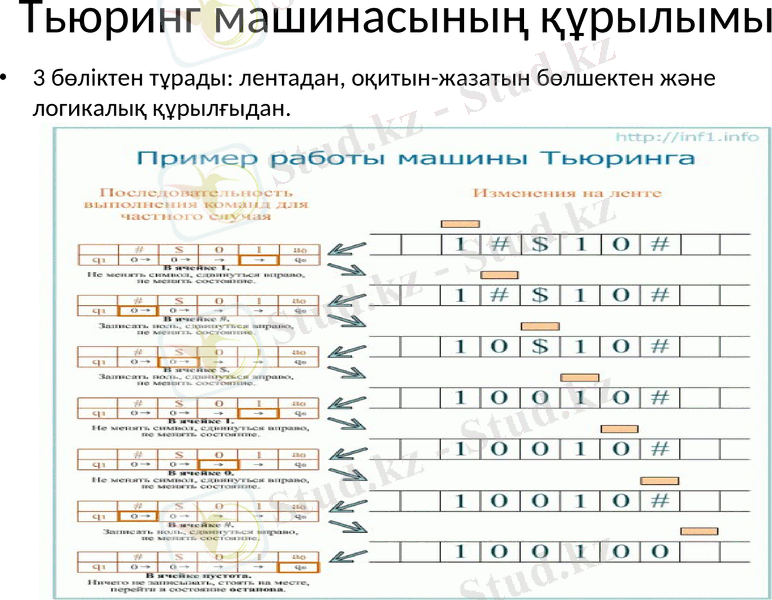
Тьюринг машинасының құрылымы
• 3 бөліктен тұрады: лентадан, оқитын-жазатын
бөлшектен және логикалық құрылғыдан.
• Мысал:
N көпразрядты санының ондық санау жүйесінде
жазылуы берілген.
n+ 1 мәнін есептеуді орындайтын Тьюринг
машинасын құрайық:
А={0,1,…,9,0,} сыртқы алфавитін қолданамыз, ондағы
символы бос таңбаға сәйкес келеді. Ішкі алфавит
алдыңғы мысалдағы сияқты екі күйде – жұмысшы (q)
және тоқтату (z) (Q={q,z}) болады. Берілген n саны,
сондай-ақ нәтиже - n+ 1 – ондық жүйеде жазылады,
цифрлар бірден көрші ұяшықтарға бос орынсыз
орналасады.
A 0 1 Функционалдық
2 3 4 5 схеманы
6 7 кесте
8 түрінде
көрсетейік:
Q z1 z2 z3 z4 z5 z6 z7 z8 z9 q0 z1
S S S S S S S S S L S
Марковтың нормальды алгоритмдері.
• Бірінен-бірі тәуелсіз тарихи пайда болған бұл тәсілдер, со ңыра
өзара эквивалентті болып шықты. Алгоритм ұғымын т ұрпаттандырудың
негізгі мақсаты мынада: әртүрлі математикалық есептердің алгоритмдік
шешімділігі мәселесін шешуге жол ашу, яғни есеп шешіміне әкелетін
алгоритм құруға бола ма?- деген сұраққа жауап беру. Біз осы мәселені ң
қойылуын және есептердің алгоритмдік шешімділігі теориясыны ң кейбір
нәтижелерін қарастырамыз, бірақ алдымен Пост, Тьюринг машиналары ж әне
Марковтың нормалы алгоритмдері мысалында автоматтар теориясында ғы
алгоритм ұғымын тұлғатандыруды, сонан соң рекурсивті функциялар
теориясы негіздерін талқылаймыз.
• Өздеріне арналған программалардың қасиеттері туралы әртүрлі
тұжырымдауды дәлелдеуге арналған абстракты ( яғни шын емес, тек қиялда
ғана бар) Пост пен Тьюринг машиналарын американдық математик Эмил
Пост пен ағылшын математигі Аллан Тьюринг бірінен-бірі т әуелсіз (ж әне іс
жүзінде бір уақытта) 1936 ж. ұсынды. Бұл машиналар бастапқы
мәліметтерді “енгізіп”, программалар орындалғаннан со ң нәтижені о қу ға
мүмкіндік беретін, толығымен анықталған әмбебап орындаушылар болып
табылады. Пост машинасы аса танымал емес, біра қ Тьюринг машинасына
қарағанда әлдеқайда қарапайым.
Тьюринг машиналарының композициясы

Осы уақытқа дейін әртүрлі алгоритмдер командалар жиыны
мен ішкі және сыртқы әріппелерімен өзгешеленетін
әртүрлі Тьюринг машиналарында орындалады деп келді.
Дегенмен, кез келген Тьюринг машинасының кез келген
алгоритмін орындауға қабілетті әмбебап Тьюринг
машинасын жасауға болады. Бұған әмбебап машинаның
сырт әріппесіндегі кез келген берілген Тьюринг
машинасының конфигурациясы мен программасын кодтау
арқылы қол жеткізуге болады.
• Кодтаудың өзі былай орындалуға тиіс:

а) әртүрлі таңбалар әртүрлі кодтық топтармен алмастырылуы
қажет, бірақ бір таңба қай жерде кездескеніне қарамай, бір
ғана кодтық топпен жаппай ауыстырылуы қажет;

б) кодтық жазба жолдары жеке кодтық топтарға бірмәнді
бөлшектенуге тиіс

с) А,П,С командаларына сәйкес кодтық топтарды тану, сыртқы
әріппеге және іш күйлеріне сәйкес кодтық топтарды ажырату
Қорытынды:
Тьюринг машинасы – белгілі бір есептерді шығару ға арнал ған қата ң
математикалық құрылым, математикалық аппарат. Бұл аппарат машина деп
аталу себебі оның құрамдас бөлігінің және функцияларының есептеу
техникасына ұқсауында. Тьюринг машинасының есептеу техникасынан
ерекшелігі оның еске сақтау құрылғысы шексіз лентадан т ұруында, ал
есептеу техникасының еске сақтау құрылғысы қаншалықты үлкен
көлемді болса да шектеулі. Сондықтан Тьюринг машинасын лентасы шексіз
болғандықтан есептеу техникасы түрінде қолдану ға болмайды.
Марковтың нормальды алгоритміне қойылатын талаптар: алгоритм
қарапайым орындалатын саны шектеулі ережелерден т ұруы тиіс, я ғни
жазбалардың шектеулі болуы талабын қанағаттандыруы тиіс; алгоритм
шектеулі қадамнан соң есепті шешуі тиіс, яғни әрекеттерді ң шектеулі болу
талабын қанағаттандыруы тиіс; алгоритм барлы қ мүмкін болатын
бастапқы деректер үшін біреу ғана болуы керек, яғни әмбебапты қ талабын
қанағаттандыруы тиіс; алгоритм қойылған есепті ң дұрыс шешімін табуы
керек, яғни дұрыс болу талабын қанағаттандыруы тиіс. Б ұл
анықтамаларда әрекетті орындаушы көрсетілуі тиіс ж әне ол орындайтын
«қарапайым» операцияларға не жататыны на қтылануы тиіс. Алгоритмді
әртүрлі формада бейнелеуге , яғни беруге болады.
Қолданылған ақпарат көздері:
1. А.Шәріпбаев «Информатика» , Алматы, 1992
2. О. Камардинов «Информатика», Алматы,2006
3. studopedia.ru/5_164228_algoritm-abstraktili-m.
4. rankw.ru/k/тьюринг+машинасы/
5. Алгоритмдер теориясы: Оқу –әдістемелік кешен.
Б.Д.Сыдықов. Алматы: Нур-Принт, 2012 жыл, 145 бет

Ұқсас жұмыстар

Тьюринг тезисі және оның негіздемесі

Тьюринг машинасы. Тьюринг тезисі және оның негіздемесі. Марковтың нормальды алгоритмы. Нормальдау принциптері және оның негіздемесі. Марковтың нормальды алгоритмі және Тьюринг машинасының композициясы

Тьюринг машинасы. Тьюринг тезисі және оның негіздемесі

Тьюринг машинасы. Тьюринг тезисі жә не оның негіздемесі. Марковтың нормальды алгоритмы. Нормальдау принциптері жә не оның негіздемесі. Марковтың нормальды алгоритмі жә не Тьюринг машинасының композициясы

Тьюринг тезисі және оның негіздемесі. Марковтың нормальды алгоритмы. Нормальдау принциптері және оның негіздемесі. Марковтың нормальды алгоритмі және Тьюринг машинасының композициясы

Тьюринг машинасы. Алан Мэтисон Тьюринг

ТЬЮРИНГ МАШИНАСЫ жә не Марковтың нормальді алгоритмы

Тьюринг машинасы

Авогадро заңы. Газдардың молярлық көлемі. Газдардың салыстырмалы тығыздығы

Программалау тілдері туралы ақпарат

Пәндер