Комбинаторика мен Ньютон биномы және олардың ықтималдықта қолданылуы

Презентация қосу

Сабақтың тақырыбы

Комбинаторика мен Ньютон
биномы және олардың
ықтималдықта қолданылуы
Күтілетін нәтиже
• Тақырыптың жаңа терминдерімен жұмыс жасай
алады; комбинаторика ұғымын біледі;
комбинаториканың орналастырулар, алмастырулар,
терулер бөлімдерінің ұқсастықтары мен
айырмашылықтарын атап, ажырата алады және
белгіленуін біледі; өздігінен және жұппен жұмыс
жасай отыра, өмірмен байланысын ұғынады; ойын
ашық айта алады
• Сандар теориясының кейбір сұрақтарын терең
зерттеу, факториялды есептей білу.
• Олимпиадалық дайындық. Жұмыстың бұл түрі
олимпиадаларға қатысатын оқушыларға қызық және
пайдалы, себебі конкурстық есептерді шығару үшін
мектеп бағдарламасы негізінде білім жетіспейді
Сабақ 3 деңгейлі бөлімнен
тұрады

Анықтамалармен сырласу

Формуланы табайық

Кім жылдам?
Анықтамалармен сырласу
Орналастырулар дегеніміз не?

Алмастырулар дегеніміз не?

Терулер дегеніміз не?

Биномдық коэффициент
дегеніміз не?
Анықтамалармен сырласу
• Анықтама: n элементтен алынған m-нен
құралған орналастырулар деп берілген n
элементтерден әр топта m элемент
(m озгешелігі ең болмағанда элементтерінің
біреуінің өзгешелігінде немесе
элементтерінің алыну ретінде болатын
қосылыстар (комбинациялар) топтарын
айтамыз
Анықтамалармен сырласу
• Анықтамасы: n элементтен жасалған
алмастырулар деп n элементтен алынған
n-нен жасалған орналастыруларды айтады.
Анықтамалармен сырласу
• Анықтама: n элементтен алынған m-нен
құралған терулер деп бір-бірінен тек
құрамымен ғана ерекшеленетін m
элементтерден тұратын комбинациялар
тобын аталады
Анықтамалармен сырласу
• Ньютон биномының
формуласындағы коэффициент
биномдық коэффициент деп
аталады
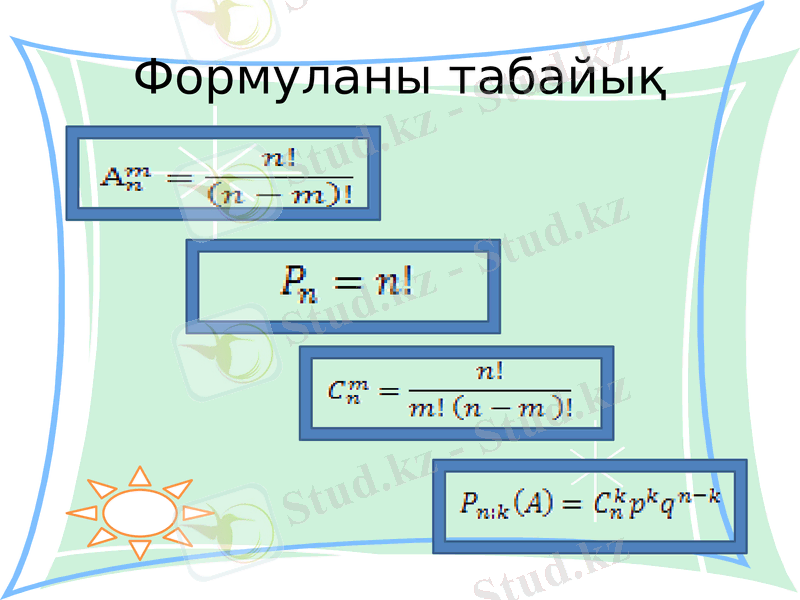
Формуланы табайық
Формуланы табайық
• Орналастырулар
Формуланы табайық
• Алмастырулар
Формуланы табайық
• Терулер
Формуланы табайық
• Бернулли формуласы
Кім жылдам?

Комбинаторика 10 20 30 40

Ньютон биномы 10 20 30 40
Кім жылдам?
• Есеп. Шахмат турниріне 12
ойыншы қатысты және әрбір
шахматшы өзгелермен бір-бір
ойыннан ойнайды. Турнирде
барлығы неше партия ойналды?
Кім жылдам?
• Талдау: Әрбір партияны өткізуге
екі ойыншы қатысады. Онда
барлық өткізілген партиялар саны
12-ден 2 бойынша алынған
терулер санына тең.
2 12! 10! 11 12 11 12
C
12 66
2!10! 10! 2 1 2
Кім жылдам?
• Есеп. Бес адамды кезекке неше
түрлі тәсілмен тұрғызуға болады?
Кім жылдам?
• Талдау: Бізге қажетті сан 5
элементтен алынған барлық
алмастырулар санына тең.

P5 5! 5 4 3 2 1 120
Кім жылдам?
• Есеп. Үш таңбалы саннан қанша
әртүрлі цифрдан құрастырылған
үш таңбалы сан алуға болады?
Кім жылдам?

P3 3! 3 2 1 6
Кім жылдам?
• Есеп. 4 оқушыны 7 орындыққа
неше түрлі тәсілмен отырғызып
шығуға болады?
Кім жылдам?
• Талдау: Мұнда Х жиыны 7
элементтен тұрады. Онда бізге
қажетті сан барлық 7-ден 4
бойынша қайталанбайтын
орналастырулар санына тең.
Өйткені бірнеше оқушы бір
орындыққа
A 7 7 отырмайды
6 5 4 деп
840
есептейміз.
Кім жылдам?

(2t + 3/t)4.
қосылғыштарға жикте
Кім жылдам?
Кім жылдам?

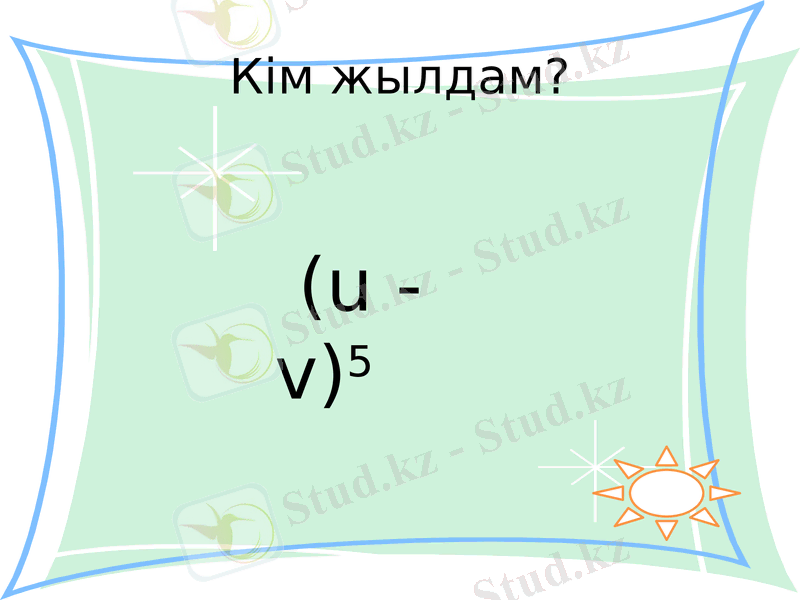
(u - v) 5
Кім жылдам?
• (u - v)5 = [u + (-v)]5 = 1(u)5 + 5(u)4(-
v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-
v)4 + 1(-v)5 = u5 - 5u4v + 10u3v2 -
10u2v3 + 5uv4 - v5.
Кім жылдам?

• (x2 - 2y)5.
Кім жылдам?
Кім жылдам?

• (2/x + 3√x)4
Кім жылдам?

• (2/x + 3√x)4 =
16/x4 + 96/x5/2 +
216/x + 216x1/2 +
81x2.
ах мет
з ғ а р
а р ы ң ы
а з а р л
Н

Ұқсас жұмыстар

Теру қасиеттері

Ньютон биномы

Комбинаторика ғылым ретінде

Математиканы оқыту әдістемесі Комбинаторика элеметтері. Логикалық есептер

Комбинаторика элементтері

Толқындардың интерференция құбылысы

Мектептегі дискретті математика элементтерін оқыту әдістемесі

Анықталған интегралдың қолданылуы

Анықталған интеграл. Анықталған интегралдың бар болу шарты. Анықталған интегралдың негізгі қасиеттері. Орта мән туралы теорема. Ньютон-Лейбнец формуласы. Анықталған интегралды интегралдау әдістері. Анықталған интегралдың қолданылуы

ТУЫНДЫ ҰҒЫМЫН ОҚЫП ҮЙРЕНУДЕ ТАРИХИ МАҒЛҰМАТТАРДЫ ПАЙДАЛАНУ

Пәндер