Виет теоремасы туралы ақпарат

Презентация қосу

Шымкент қаласының №79 орта мектебі

Виет теоремасы

Алгебра 8 сынып

Математика пәнінің мұғалімі: Ахметова Ж. К.
Сабақ мақсаты:

1. Виет теоремасын тұжырымдау және дәлелдеу.
Квадрат теңдеулерді түбірлердің қасиеттерін
қолдану арқылы шешуді үйрету;

2. Оқушыларға Виет теоремасын қолдану
тәсілдерімен таныстыру және квадрат
теңдеулерді шешуді үйрету;

3. Виет теоремасын қолдана отырып есептер
шығаруға оқушыларды баулу және дағдыландыру.
Қайталау сұрақтары:
1. ах 2 bx c 0 түріндегі теңдеу қалай
аталады?
b 4ac
2. формуласымен есептелетін сан қалай
аталады?
3. Егер D>0 болса, онда квадраттық теңдеудің неше түбірі
болады?
4. Егер D=0 болса, онда квадраттық теңдеудің неше түбірі
болады?
5. Егер D<0 болса, онда квадраттық теңдеудің неше түбірі
болады?
6. Қ2 х 2 жа
андай 5 хғдайда
3 квадратты
0 қ теңдеу келтірілген квадраттық
теңдеу деп атайды?
7. те ңдеуіні ң коэффициенттерін атап
шығыңдар.
8. Егер квадраттық теңдеуінде коэффициенттердің бірі – b не с
немесе b мен с-ның екеуі де 0-ге тең болса, мұндай теңдеулерді
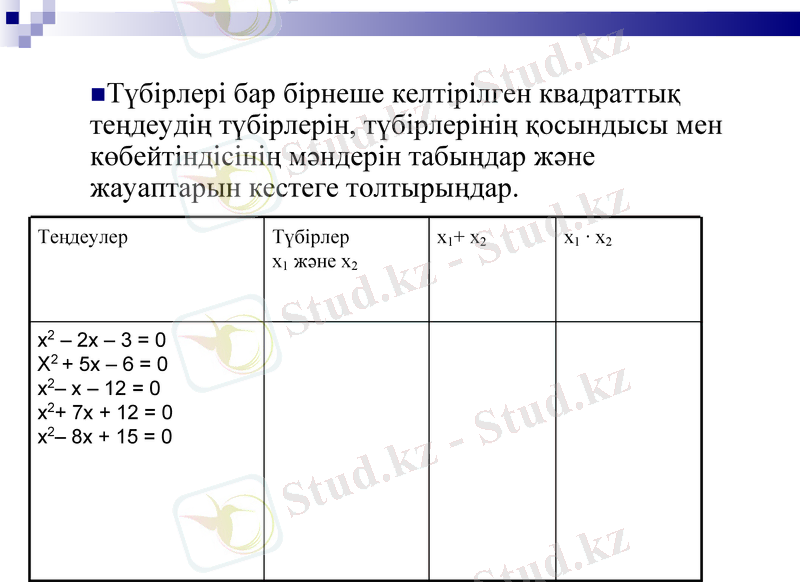
Түбірлері бар бірнеше келтірілген квадраттық
теңдеудің түбірлерін, түбірлерінің қосындысы мен
көбейтіндісінің мәндерін табыңдар және
жауаптарын кестеге толтырыңдар.
Теңдеулер Түбірлер х1+ х2 х1 · х2
х1 және х2
х2 – 2х – 3 = 0
Х2 + 5х – 6 = 0
х2– х – 12 = 0
х2+ 7х + 12 = 0
х2– 8х + 15 = 0
Бұл мысалдардан, келтірілген квадраттық теңдеу
түбірлерінің қосындысы қарсы таңбасымен
алынған екінші коэффициентке, ал көбейтіндісі бос
мүшеге тең екенін байқадық.
Енді бұл қасиетті теорема ретінде тұжырымдап
шығайық.
Теорема : Келтірілген квадраттық теңдеу
түбірлерінің қосындысы қарсы таңбасымен
алынған екінші коэффициентке, ал көбейтіндісі
бос мүшеге тең болады:

х1 х2 p; x1 x2 q
x 2 px q 0 (келтірілген квадрат теңдеу)
p – екінші коэффициент
q – бос мүше
Теңдеудің дискриминанті: D p 4q
р D р D
Егер D>0, онда теңдеудің екі түбірі бар: х1 және х2
2 2
р D р D 2p
Түбірлердің қосындысы: х1 х2 p
2 2

( р D ) ( р D ) ( p) 2 ( D ) 2
Түбірлердің көбейтіндісі: х1 х2
2 2 2
2 2 4
p D p ( p 4q )
q . Сонымен, х1 х2 p
4 4
х1 х2 q
Бұл теореманы бірінші дәлелдеген француз математигі
Француа Виет (1540-1603) болғандықтан, соның
атымен аталады.
Кейбір есептерді шешкенде Виет теоремасына кері
теореманы қолданады.
Теорема (кері теорема). Егер p, q, x1 , x2 сандары
үшін х1 х2 p, x1 x2 q шарттары орындалса,
онда x1 мен x2 сандары х px q 0
теңдеуінің түбірлері болады.
Виет теоремасы және оған кері теорема теңдеуді
шешпей-ақ , түбірлерінің қосындысы мен
көбейтіндісін табуға және түбірлері белгілі
болғанда, теңдеуді құруға мүмкіндік береді.
Мысал қарастырайық:
Түбірлері õ1 2 3 және õ2 2 3
болған квадраттық теңдеуді құрайық:
õ2 ( 2 3 2 3 ) õ ( 2 3 )(2 3) 0
õ 4 õ 1 0
№257

Теңдеулер Түбірлерінің Түбірлерінің
қосындысы көбейтіндісі

õ2 2 õ 35 0

õ2 4 õ 3 0

õ2 8 õ 7 0

õ2 8 õ 9 0

õ2 10 õ 11 0

õ2 4 õ 1 0
№258 Теңдеулер Түбірлерінің Түбірлерінің
қосындысы көбейтіндісі
х 2 24 х 23 0

у 2 44 у 300 0
х 2 120 х 0
у 2 12 0
2 х 2 9 х 10 0

5 х 2 12 х 7 0
х 2 2 х 0
4 х 2 12 0
õ2 2 õ 35 0
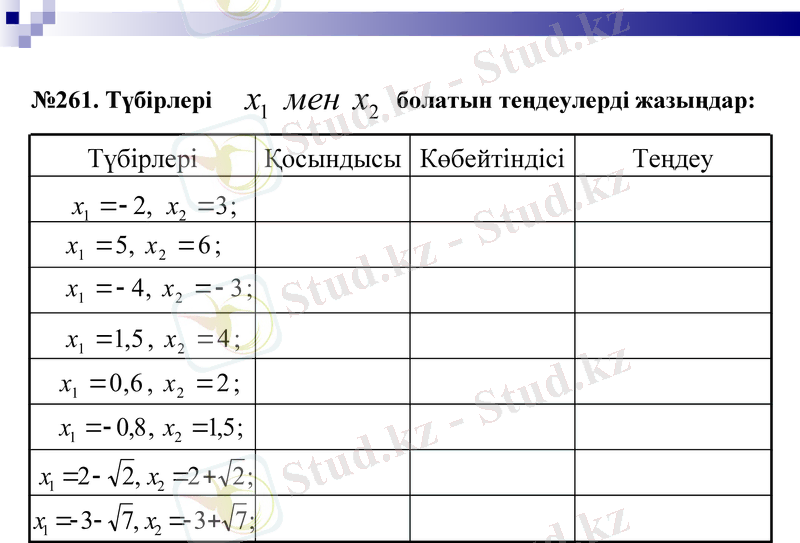
№261. Түбірлері х1 мен х2 болатын теңдеулерді жазыңдар:

Түбірлері Қосындыс Көбейтіндісі Теңдеу
ы
х1 2, х2 3 ;
х1 5, х2 6 ;
х1 4, х2 3 ;
х1 1,5 , х2 4 ;
х1 0,6 , х2 2 ;
х1 0,8 , х2 1,5 ;
х1 2 2 , х2 2 2 ;
х1 3 7 , х2 3 7 ;
1. х2 - 12х + с = 0 теңдеуінің бір түбірі х1=5.
х1+ х2=12 және х1 · х2=с. с-ны табыңдар.

2. х2 +рх + 15 = 0 теңдеуінің бір түбірі х1=3.
х1+ х2= -р және х1 · х2=15. р-ны табыңдар.

3. Теңдеулерді шешіп Виет теоремасы және кері
теорема арқылы тексеріңдер:
а) х2 - 9х + 8 = 0,
б) х2 + 12х + 20 = 0,
в) х2 - 4х - 21 = 0.
Тест сұрақтары:
1. Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:
х 2 8 х 15 0
А) 8; 15 В) -8; 15 С) 8; -15 D) -8; -15 Е) 5; -18
2. Түбірлері х1 1, х2 7 болатын те ңдеуді жазы ңдар:
А)
х 8 х 15 0 В)
х 8 х 7 0 С) х 2 8 х 7 0
х 2 8 х 7 0 х 2 8 х 7 0
D)х 2 рх 35 0 Е)
3. теңдеуінің бір түбірі 7-ге тең. Екінші түбірін және
р-ны табыңдар.
А) 2; 5 В) -2; 5 С) -5; -2 2
D) 2;х-5 Е) 5; -1.10
11 х 0
4. Теңдеудің түбірлерін табыңдар:
А) 11; 10 В) -1; 10 С) 1; 10 D) 1; -10 Е) -1; -10
2 2
5 х 8 х квадратты
5. Келтірілген 3 0 қ теңдеуді
х кө8 х 15 0
рсет: 9 х 2 х 15 0
А) 2 В) 2 С)
2 х 5 х 1 0 3 х х 5 0
Теңдеулердің түбірлерінің қосындысы мен көбейтіндісін
табыңдар:
Үйге тапсырма: §3.
№259, №260 79 бет

Ұқсас жұмыстар

Теңдеудің түбірлерін табыңдар

Виет теоремасы

Таләйлі болсын талғамың

Виет теоремасын үйрену

Жұп коэффициенті бар теңдеуді шешу

Теңдеуді шеш

Квадрат теңдеулерді шешу

Кейбір тригонометриялық функциялар

Квадрат теңдеулерге қайталап есеп шығару.Виет теоремасы

Квадрат теңдеу

Пәндер