Жамбыл атындағы №5 мектеп-гимназиясының Математика және информатика кафедрасының қаңтар айлық жоспары, іс-шаралары және есептер жинағы

Скачать

1. Әдістемелік бірлестіктің айлығы туралы

Жамбыл атындағы №5 мектеп-гимназиясында барлығы 8 кафедра (әдістемелік бірлестік) жұмыс істейді. Қазан айынан мамыр айына дейін әрбір кафедра кафедра айлығын өткізеді . Математика кафедрасы қаңтар айында әдістемелік бірлестіктің іс-шараларын өткізді. Кафедрада барлығы 13 мұғалім жұмыс істейді, 9-ы математика, 4-еуі информатика пәнінің мұғалімдері. Айлық кезінде төмендегідей іс-шаралар ұйымдастырылып, өткізілді.

Тақырыбы: «Топтық және жұптық жұмыстарда оқушыларды бағалау»

Мақсаты

Топтық жұмыста өзін-өзі бағалау және өзара бағалау дағдыларын қалыптастыру.

Математика және информатика кафедрасының айлық жоспары

№

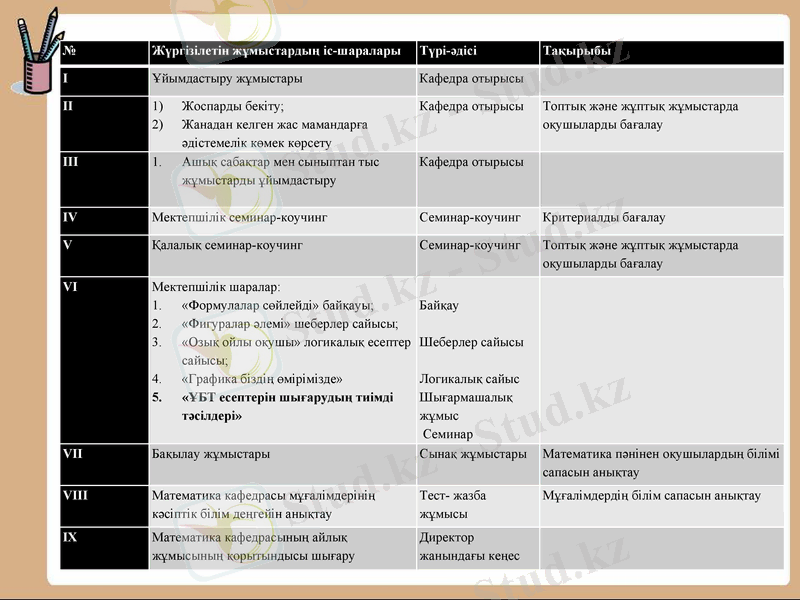
Жүргізілетін жұмыстардың іс-шаралары

Түрі-әдісі

Тақырыбы

I

Ұйымдастыру жұмыстары

Кафедра отырысы

II

Жоспарды бекіту;

Жанадан келген жас мамандарға әдістемелік көмек көрсету

Кафедра отырысы

Топтық және жұптық жұмыстарда оқушыларды бағалау

III

Ашық сабақтар мен сыныптан тыс жұмыстарды ұйымдастыру

Кафедра отырысы

IV

Мектепшілік семинар-коучинг

Семинар-коучинг

Критериалды бағалау

V

Қалалық семинар-коучинг

Семинар-коучинг

Топтық және жұптық жұмыстарда оқушыларды бағалау

VI

Мектепшілік шаралар:

«Формулалар сөйлейді» байқауы;

«Фигуралар әлемі» шеберлер сайысы;

«Озық ойлы оқушы» логикалық есептер сайысы;

«Графика біздің өмірімізде»

«ҰБТ есептерін шығарудың тиімді тәсілдері»

Байқау

Шеберлер сайысы

Логикалық сайыс

Шығармашалық жұмыс

Семинар

VII

Бақылау жұмыстары

Сынақ жұмыстары

Математика пәнінен оқушылардың білімі сапасын анықтау

VIII

Математика кафедрасы мұғалімдерінің кәсіптік білім деңгейін анықтау

Тест- жазба жұмысы

Мұғалімдердің білім сапасын анықтау

IX

Математика кафедрасының айлық жұмысының қорытындысы шығару

Директор жанындағы кеңес

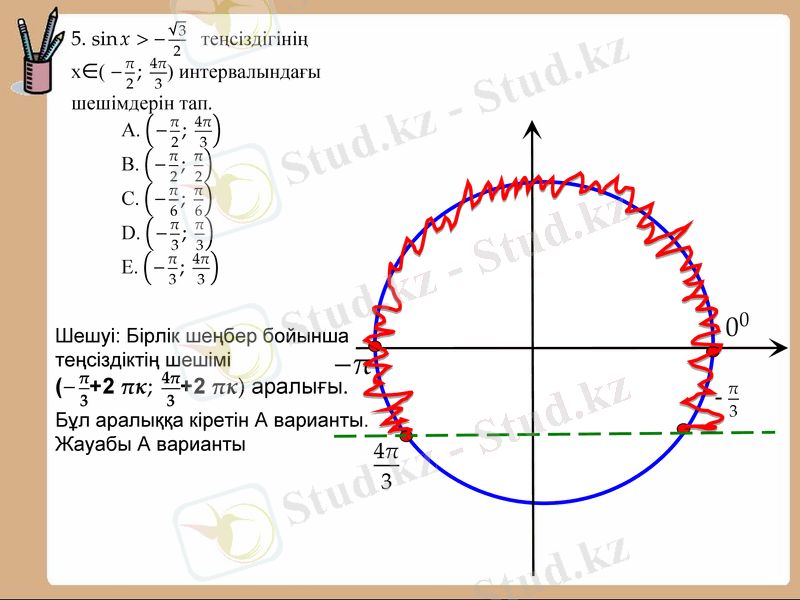
Тригонометриялық теңдеулер, теңсіздіктер және олардың жүйелерінің шешімдерін табудың тиімді тәсілдері

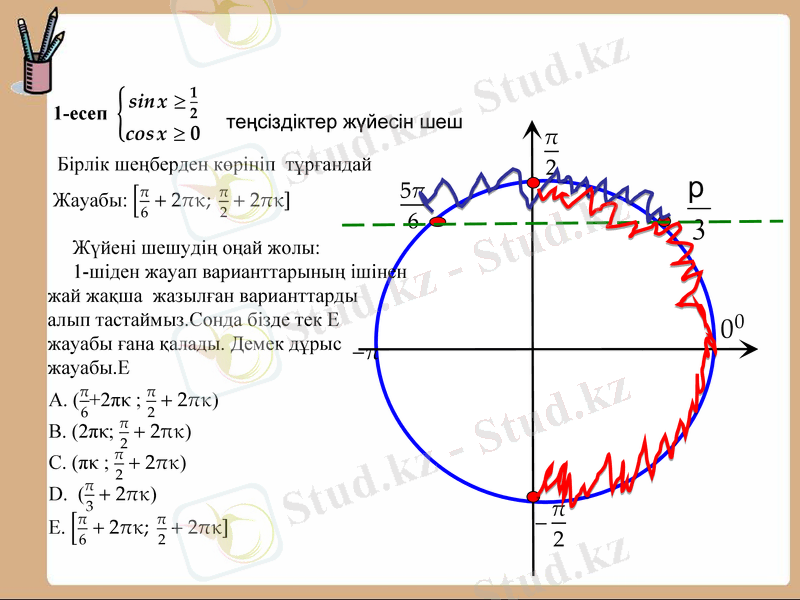
Жүйені шешудің оңай жолы:

1-шіден жауап варианттарының ішінен

жай жақша жазылған варианттарды

алып тастаймыз. Сонда бізде тек Е

жауабы ғана қалады. Демек дұрыс

жауабы. Е

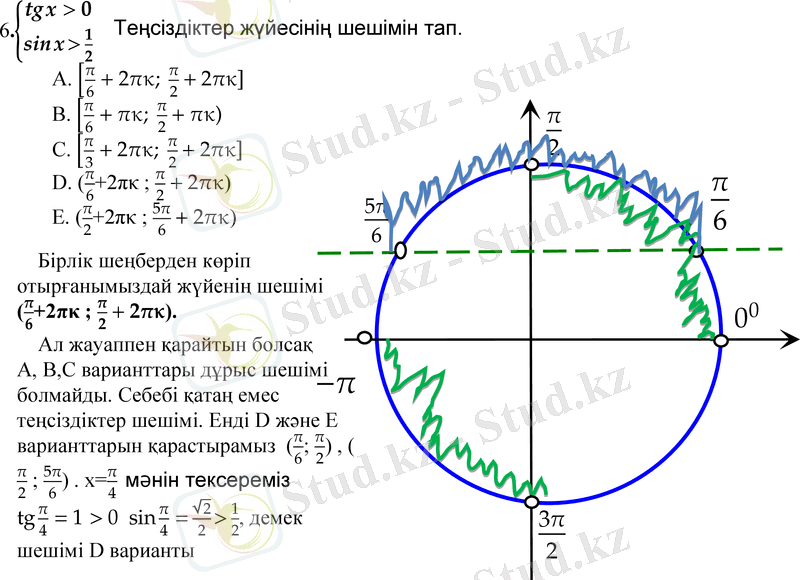
теңсіздіктер жүйесін шеш

Бірлік шеңберден көрініп тұрғандай

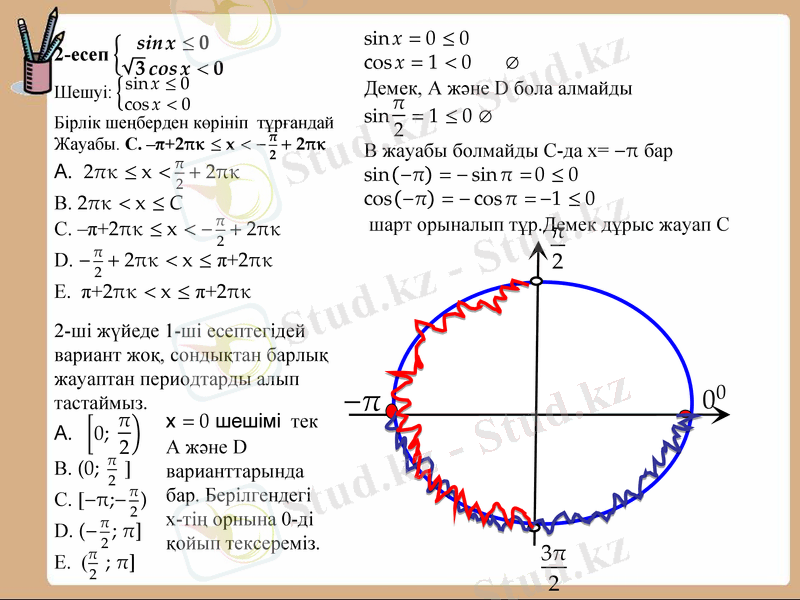
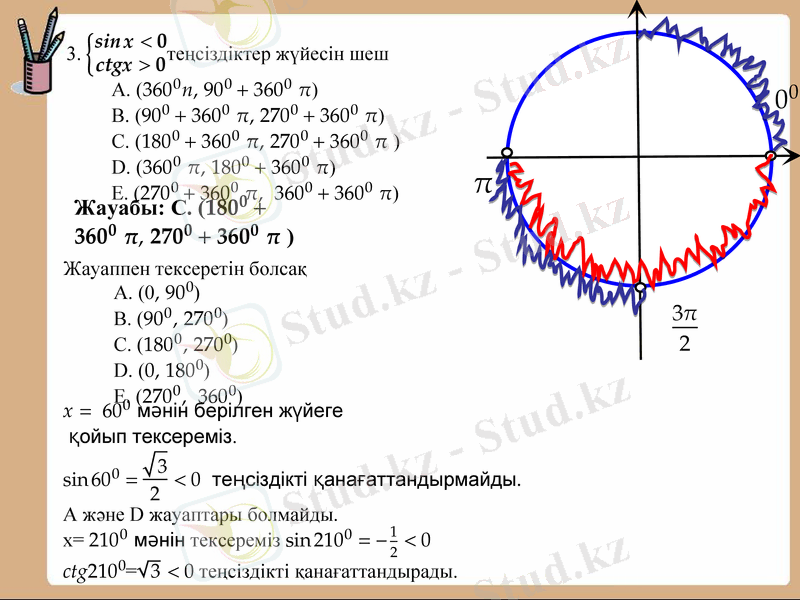
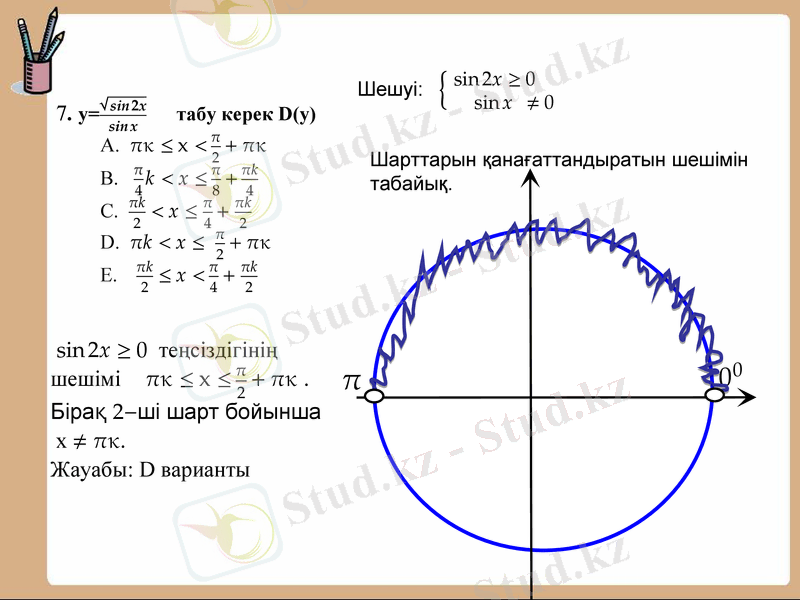
Теңсіздіктер жүйесінің шешімін тап.

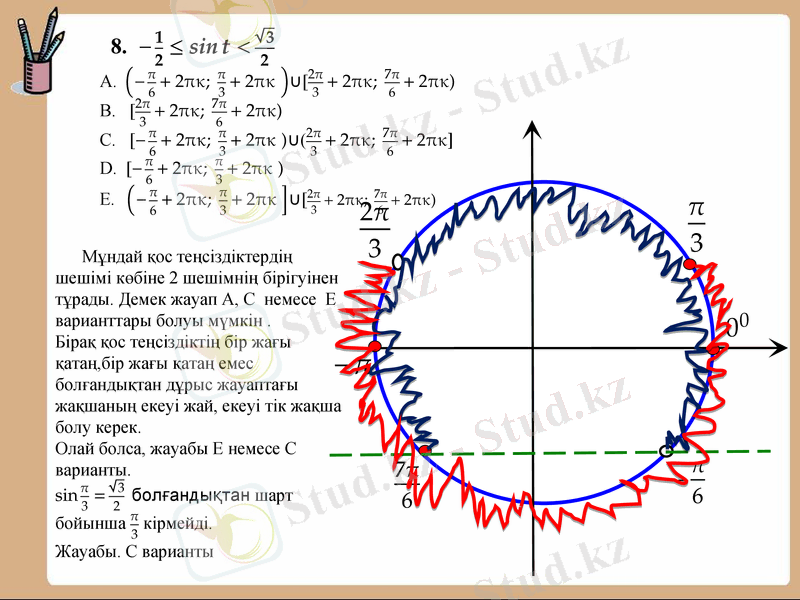
Шарттарын қанағаттандыратын шешімін табайық.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс