Негізі айнымалы болып келген көрсеткіштік және логарифмдік теңсіздіктерді шешу

Жамбыл атындағы №5

мектеп-гимназиясының 11 “Г”

сынып оқушысы

Құрманбаева Сымбат

Жобаның тақырыбы

Негізі айнымалы болып

келген көрсеткіштік

және логарифмдік

теңсіздіктерді шешу

Мақсаты:

Көрсеткіштік және логарифмдік теңсіздіктерді шешу кезеңдерін оқып-үйреніп, шешудің әр түрлі әдістерін білу

Зерттеу жаңалығы:

Жұмыста негізі айнымалы болып келген кейбір логарифмдік теңсіздіктерді шешудің оқулықтарда және талапкерлерге арналған әдебиеттерде келтірілген тәсілдерден басқа тиімді жолы көрсетілген.

Логарифмнің негізгі қасиеттері

1. , (a > 0, a  1) - негізі а болатын бір санының логарифмі нөлге тең;

2. , (a > 0, a  1) - негізі а болатын а санының логарифмі бірге тең;

3. , (a > 0, a  1) , b > 0, с > 0 екі немесе бірнеше оң сандардың

көбейтіндісінің логарифмі көбейткіштердің логарифмдерінің қосындысына тең;

4. , (a > 0, a  1, b > 0, с > 0) қатынастың немесе бөлшектің

логарифмі алымының логарифмі мен бөлімінің логарифмінің айырымына тең;

5. , (a > 0, a  1, b > 0) дәреженің логарифмі дәреже көрсеткішін

дәреже негізінің логарифміне көбейткенде тең;

6. , (a > 0, a  1, b > 0)

7. , (a > 0, a  1, b > 0, с > 0, с  1) жаңа негізге көшу формуласы;

8. , (a > 0, a  1, b > 0, b  1) ( 7-қасиеттің дербес жағдайы) ;

9. , (a > 0, a  1, b > 0)

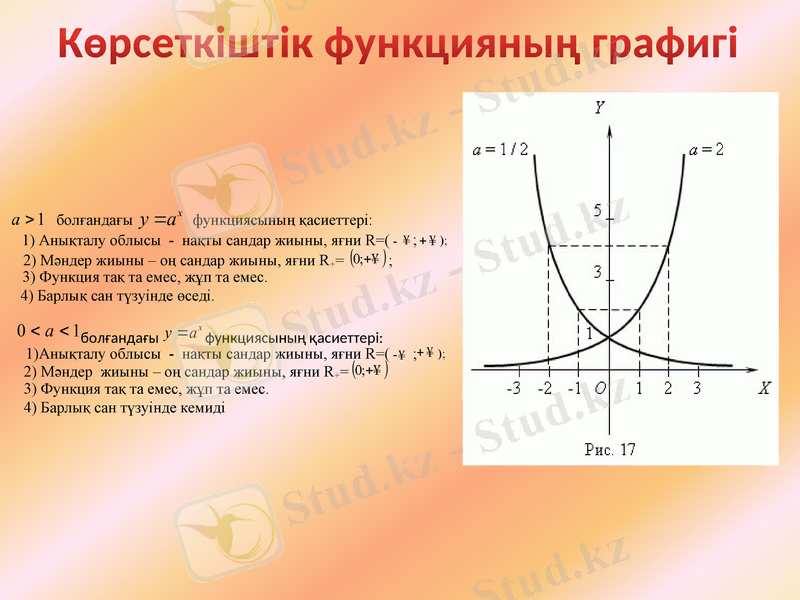
3) Функция тақ та емес, жұп та емес.

4) Барлық сан түзуінде өседі.

болғандағы функциясының қасиеттері:

болғандағы

функциясының қасиеттері:

1) Анықталу облысы - нақты сандар жиыны, яғни R=( -

;

) ;

2) Мәндер жиыны - оң сандар жиыны, яғни R+=

;

1) Анықталу облысы - нақты сандар жиыны, яғни R=( -

;

) ;

2) Мәндер жиыны - оң сандар жиыны, яғни R+=

3) Функция тақ та емес, жұп та емес.

4) Барлық сан түзуінде кемиді

Көрсеткіштік функцияның графигі

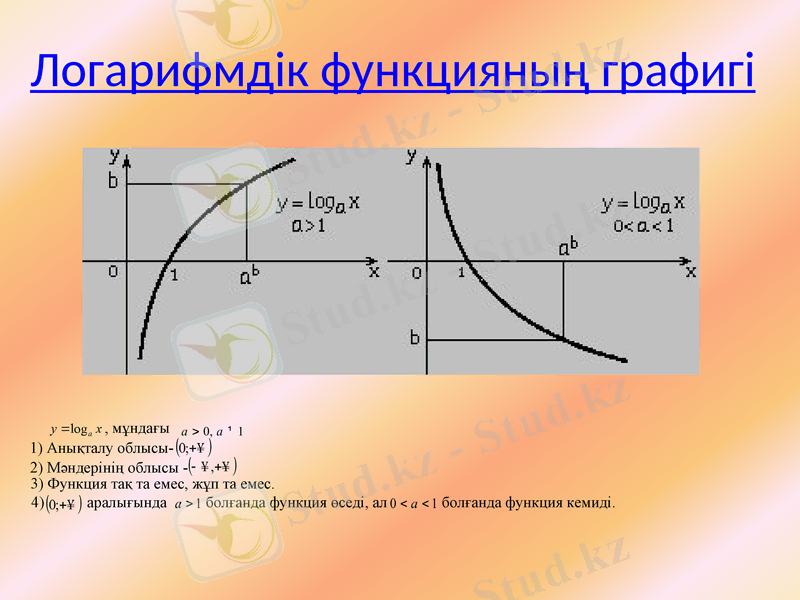
3) Функция тақ та емес, жұп та емес.

4) аралығында болғанда функция өседі, ал болғанда функция кемиді.

Логарифмдік функцияның графигі

, мұндағы

1) Анықталу облысы-

2) Мәндерінің облысы -

1. Сан түзуіне f(x) функциясының барлық нөлдері мен үзіліс нүктелерін боялмаған

дөңгелекшелермен белгілейді.

2. а) функцияның барлық жұп дәрежелі көбейткіштерін алып тастайды.

б) функцияның тақ дәрежелі көбейткіштері бірінші дәрежелі көбейткіштерге ауыстырылады.

в) бөлшектің алымы мен бөлімінде бірдей көбейткіштер қалса, оларды шығарып тастайды.

3. Соңғы теңсіздіктегі функцияның нөлдері мен үзіліс нүктелерінің ең үлкенінің оң жағынан, сан

өсінің үстіндегі кез келген нүктеден шығатын,

f(x) функциясының нөлдері мен үзіліс нүктелері арқылы өтетін толқын сызық жүргізіледі.

4. Егер теңсіздік f (x) < 0 болса, онда осы толқын сызық астында жататын аралықтар берілген

түрдегі теңсіздіктің шешімі.

f(x) =

>0, немесе f(x) <0, немесе f(x)

0, немесе f(x) 0

түрдегі теңсіздіктерді интервалдар тәсілімен шешу

Негізі айнымалы болып келген логарифмдік теңсіздік

(1) теңсіздігі өзінің анықталу облысында

(2)

келесі теңсіздік мәндес:

(3) яғни, болса, онда

(4)

Дәлелдеуі. Айталық, (2) шарт орындалсын. Онда

дәлелденді.

Теңсіздікті шешудің алгоритмі:

1. (2) жүйені шеше отырып, теңсіздіктің анықталу облысын (D) табамыз. .

2. (3) теңсіздікті шешіп, шешімдер жиынын А арқылы белгілейміз.

3. (2) жүйе мен (3) теңсіздіктің шешімдер жиынының қиылысуын,

яғни жиынын анықтаймыз.

Мысалы. Теңсіздікті шешіңіз

1-тәсіл. [2, 72б] Шешуі.

берілген теңсіздік келесі жүйелер жиынтығына эквивалент:

(5) жүйені шеше отырып, келесі жүйені аламыз:

(7)

(7) жүйе келесі екі жүйелер жиынтығына эквивалент:

(8)

(9)

(8) жүйенің шешімі жоқ. (9) жүйенің шешімі

(6) жүйені шеше отырып, келесі жүйені аламыз

немесе

(10) яғни,

Жауабы:

Ұсынылған алгоритмді пайдаланып шешу.

1. Жүйені шеше отырып, теңсіздіктің анықталу облысын анықтаймыз.

Сонымен, анықталу облысы

эквиваленттілікті ескере отырып, берілген теңсіздіктің орнына

теңсіздігін аламыз. Интервалдар әдісін пайдалана отырып, теңсіздіктің шешімін табамыз:

3. А және D жиындарының қиылысуын анықтаймыз:

Жауабы:

Ескерту: Жауапқа анықталу облысына енбейтін x=0 нүктесі қате енгенін оңай байқауға болады. Бұл қате (6) жүйені оған эквивалент емес (10) жүйемен алмастырғаннан туды.