Еркін материялдық нүктенің динамикасы

2- дәріс.

Динамиканың негізгі түсініктері мен анықтамалары.

1. Еркін материялық нүкте қозғалысының дифференциалдық теңдеулері.

2. Нүкте динамикасының негізгі екі есебі.

Динамиканың негізгі түсініктері мен анықтамалары

Динамика деп теориялық механиканың денеге түсірілген күштер мен олардың әсерінен болатын

қозғалыс арасындағы тәуелділікті зерттейтін бөлімін айтады.

Осы бөлімдегі негізгі ұғымдардың бірі - дененің массасы. Масса - дененің инерттілігін сипаттайтын шама. Динамикада қозғалысы зерттелетін қарапайым объект - материялық нүкте. Материялық нүкте деп берілген есеп жағдайында өлшемдерін ескермеуге болатын белгілі массасы бар геометриялық нүкте деп қарастыруға болатын дене. Қозғалысы еш бағытта шектелмейтін материялық нүкте еркін нүкте деп аталады.

Динамиканың негізгі түсініктері мен анықтамалары

1 - аксиома. (Ньютонның бірінші заңы) Егер еркін материялық нүктеге ешқандай күш әсер етпесе, онда ол өзінің тыныштық күйін немесе түзу сызықты бірқалыпты қозғалысын сақтайды. Бұл аксиома екпін заңы деп те аталады.

Динамиканың аксиомалары:

Динамиканың негізгі түсініктері мен анықтамалары

2 - аксиома. (Ньютонның екінші заңы) Егер еркін материялық нүктеге бір күш әсер етсе, онда ол осы күшке пропорционал үдеумен қозғалады.

Осы аксиоманы динамиканың негізгі заңы деп те атайды.

m - материялық нүктенің массасы;

оның үдеуі;

нүктеге әсер етуші күш.

Динамиканың негізгі түсініктері мен анықтамалары

Динамиканың аксиомалары:

3 - аксиома. (Ньютонның екінші заңы) Екі материялық нүкте бір-біріне модульдері тең, бір түзудің бойында жататын бағыттары қарсы күштермен әсер етеді.

Динамиканың аксиомалары:

4 - аксиома. Еркін материялық нүктеге бір мезетте бірнеше күштер әсер етсе, онда нүкте

әрқайсысы нүктеге беретін үдеулерінің

күштердің векторлық

қосындысына тең үдеумен қозғалады. Осы аксиома күш әсерінің тәуелсіздігі туралы заң деп те аталады.

n n

v v

m m

    1  F  R .

v 1 v 1

Бұл аксиома нүктеге әсер ететін бірнеше күшті тең әсерлі күшпен алмастыруға болатындығын көрсетеді.

1, 2, 4 - аксиомалардағы орындалатын координат жүйелерін екпіндік жүйе деп атайды.

Динамиканың негізгі түсініктері мен анықтамалары

(3)

Динамиканың негізгі түсініктері мен анықтамалары

Динамиканың аксиомалары:

m  F a  N,

F a  

5 - аксиома. Еркін емес нүктедегі байланыс әсерлерін байланыс реакцияларымен алмастырып, нүктені еркін нүкте ретінде қарастыруға болады.

нүктеге әсер ететін берілген күштердің тең

әсерлі күші, (бұл күштерді актив күштер деп

атайды) ;

N - байланыс реакцияларының тең әсерлі күші.

(4)

1 ВЕКТОРЛЫҚ ТҮРІ

Материялық нүкте қозғалысының дифференциалдық теңдеулері

(5)

- нүктеге әсер етуші күштердің бас

векторы, нүктенің

жалпы жағдайда ол орнына, жылдамдығына

және уақытқа тәуелді болуы мүмкін

Материялық нүкте қозғалысының дифференциалдық теңдеулері

2 КООРДИНАТТЫҚ ТҮРІ

(6)

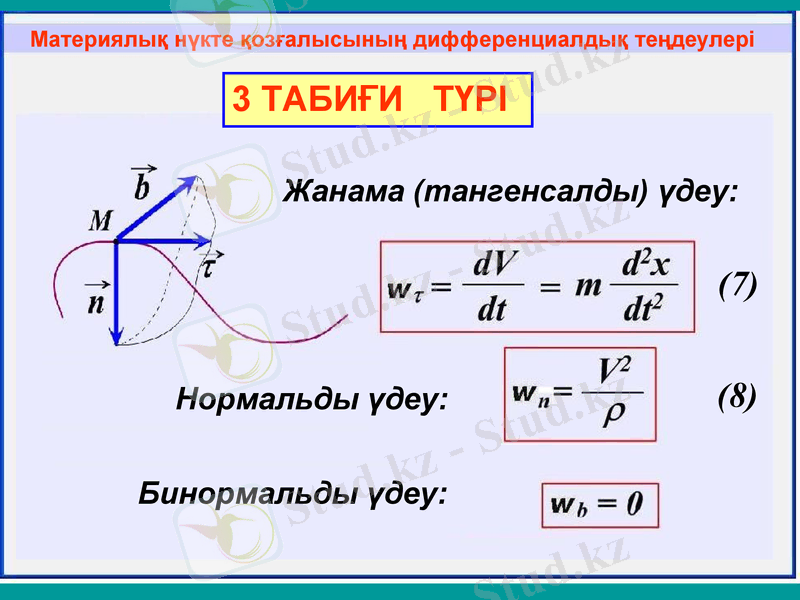
3 ТАБИҒИ ТҮРІ

Материялық нүкте қозғалысының дифференциалдық теңдеулері

Нормальды үдеу:

Бинормальды үдеу:

Жанама (тангенсалды) үдеу:

(7)

(8)

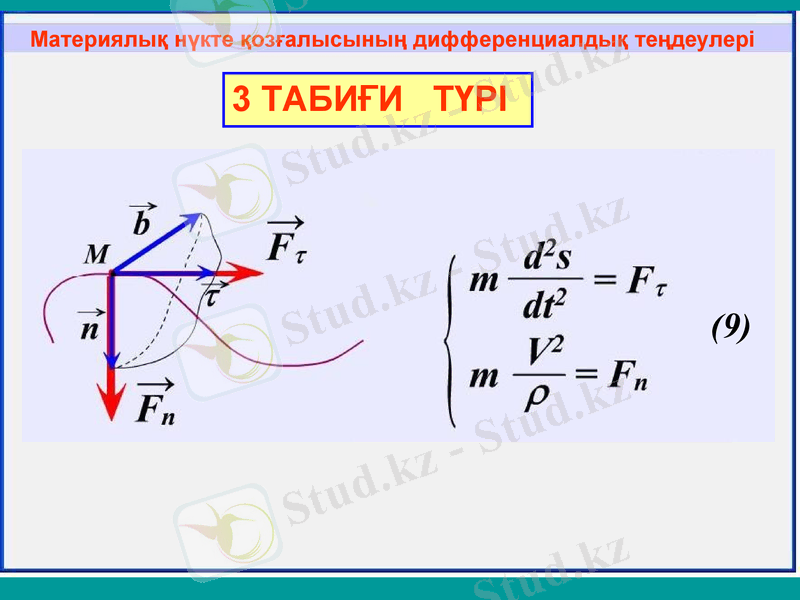
Материялық нүкте қозғалысының дифференциалдық теңдеулері

3 ТАБИҒИ ТҮРІ

(9)

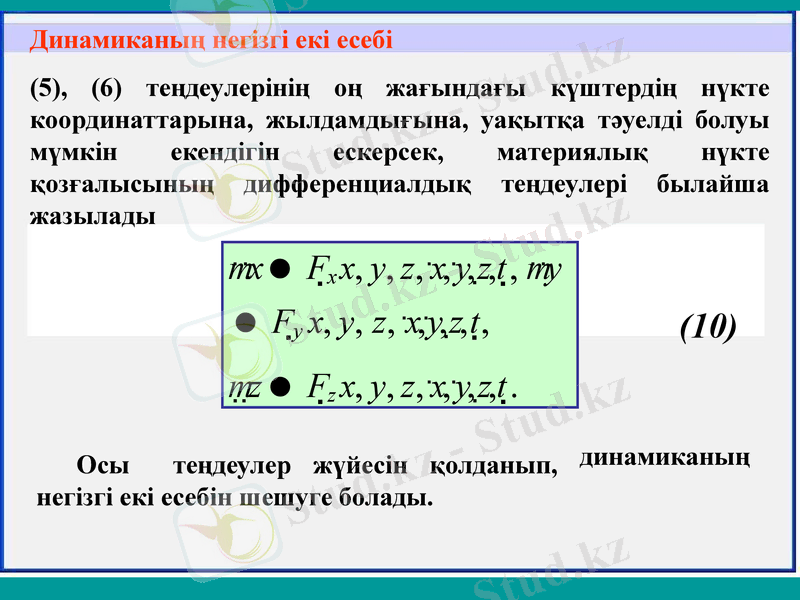
Динамиканың негізгі екі есебі

(5), (6) теңдеулерінің оң жағындағы

күштердің нүкте

координаттарына, жылдамдығына, уақытқа тәуелді болуы

мүмкін екендігін ескерсек,

материялық теңдеулері

нүкте былайша

қозғалысының дифференциалдық жазылады

динамиканың

mx  Fx x, у, z, x, у, z, t , my  Fу x, у, z, х, у, z, t ,

mz  Fz x, у, z, x, у, z, t .

Осы теңдеулер жүйесін қолданып, негізгі екі есебін шешуге болады.

(10)

Динамиканың негізгі екі есебі

Динамиканың екінші (кері) есебі

Алғашқы

шарттар

бойынша,

берілген

күштер әсер

ететін

массасы

белгілі

материялық

нүктенің

қозғалыс

заңдылығын

анықтау. Алғашқы шарттар деп уақыттың алғашқы мезетіндегі нүктенің орны мен оның жылдамдығы аталады.

Динамиканың бірінші (тура) есебі

Массасы белгілі, берілген заңдылықпен қозғалатын материялық нүктеге әсер етуші күштерді анықтау

бірінші есебін

шешу үшін

Нүкте динамикасының

берілген нүкте қозғалысының

кинематикалық

теңдеулерінен уақыт бойынша екінші ретті туынды алып,

(6) немесе (10) теңдеулер жүйесін тұрғызып, оны шеше отырып ізденді күштің өстерге проекцияларын табамыз

Fx  mx, Fy  mу, Fz  mz.

Осы күш проекциялары арқылы күштің модулі мен бағыты анықталады.

Динамиканың негізгі екі есебі

(11)







t; C, C

z  f 

3 1 2 6

2 1 2 6

, , C .

 y  f t; C, C, , C ;

Динамиканың негізгі екі есебі

Нүкте динамикасының екінші есебін шешу (6) немесе (10) дифференциалдық теңдеулер жүйесін құрастырып, жүйенің әрбір теңдеуін екі рет интегралдау керек. Интегралдағанда алты интегралдық тұрақтылар С1, С2, . . . , С6 пайда болып, толық шешімі мына түрде жазылады:

 x  f1 t; C1, C2, , C6 ;

Осы шешімдерден уақыт бойынша туынды алсақ, нүкте жылдамдығының проекцияларын анықтаймыз

(12)

x  f  t; C1, C2, , C6 ;

Динамиканың негізгі екі есебі







z 3 1 2 6

  f  t; C, C, , C .

 y  f2 t; C1, C2, , C6 ;

етуші күштер

бірдей

болғанмен

(12)

Әсер формуладан

шығатын жалпы

тұрақтыларға байланысты әр

шешімі интегралдық түрлі дербес шешім

болатыны көрініп тұр. Интегралдаудың белгісіз тұрақты шамалары алғашқы шарттардан анықталады, яғни уақыт

t0 болған сәттегі нүктенің орны x0, y0,

жылдамдығының проекцияларының V0x,

z0 мен

V0y, V0z

шамалары бойынша. Көбінесе t0 = 0 деп алынады.

(13)

Динамиканың негізгі екі есебі

Бастапқы шарттарды (12) және (13) теңдеулеріне қойып интегралдық тұрақтыларды анықтап, берілген шарт үшін нүктенің қозғалыс заңы анықталады







z  f t; x, y

0 z

0 y

0 x

0 0

0 y 0 z

0 0 0 x

2 0

,  .

, z, 

 y  f t; x, y, z, , ,  ;

, 

 x  f1 t; x0, y0, z0, 0 x, 0 y, 0 z ;

(14)

Сонымен,

материялық

теңдеулерінің алғашқы

нүктенің шартты

дифференциалдық қанағаттандыратын

шешімдері нүктенің нақты қозғалысын анықтайды.

Динамиканың негізгі екі есебі

Динамиканың негізгі есебін шешкенде көбіне мынадай ретті ұстаған ыңғайлы:

Координаталар жүйесін қабылдағанда координатаның басын нүктенің бастапқы орнымен беттестіріп, өстер бағыттары күш, жылдамдық пен үдеулерді проекциялауға ыңғайлап салу керек.

Қабылданған координаталар жүйесіне қарағанда қозғалыстағы нүктенің бастапқы шарттарын жазу керек.

Қозғалып бара жатқан нүктенің кез келген уақыт аралығындағы қозғалысының орнын (көбінесе, координатасы және жылдамдығы оң болатындай) салу керек.

Нүктеге әсер етуші активтік және реакция күштерін салу керек.