Материалдық нүктенің қозғалысының дифференциалдық теңдеулері, түзу сызықты тербелістер және нүкте динамикасының жалпы теоремалары

Еркін емес матерялық нүкте қозғалысының дифференциалдық теңдеулері және оны нүкте динамикасының негізгі есептерін шешу үшін қолдану

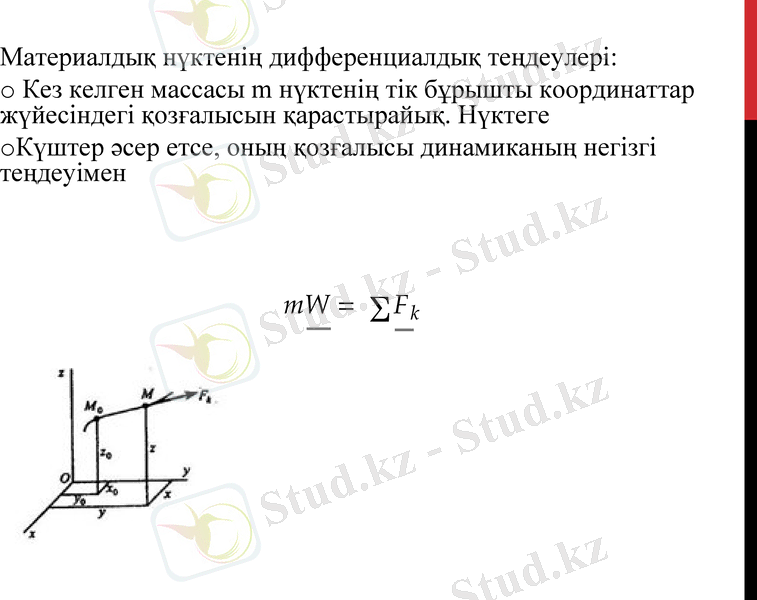
(2) -жай дифференциалдық теңдеулердің әр қайсысы екінші ретті болғандықтан, үш теңдеудің әр қайсысын интегралдағанда алты интегралдық тұрақтылар пайда болады.

МАТЕРИЯЛЫҚ НҮКТЕНІҢ ТҮЗУ СЫЗЫҚТЫ ТЕРБЕЛІСІ

Нүктенің түзу сызықты еркін тербелісі

Уақытқа байланысты қайталанып отыратын қозғалысты “тербеліс” деп атаймыз. Мысалы алтыбақан қозғалысы, бесік қозғалысы тербеліске жатады. Тербеліс қозғалыстары механикада, физикада, жалпы табиғатта кең таралған қозғалыстар. Мысалы, электронның тербелісі, серіппенің ұшына бекітілген жүк тербелісі, су-газ тербелісі, жүрек тербелісі. Тербеліс қозғалыстары қайтарушы күштер әсерінен туады. Қайтарушы күшке серіппенің серпімділік күші, тартылыс күштері, тағы да басқа күштер жатады.

НҮКТЕ ДИНАМИКАСЫНЫҢ ЖАЛПЫ ТЕОРЕМАЛАРЫ

Нүкте динамикасының есептерін шығару үшін нүкте қозғалыстарының дифференциалдық теңдеулерін интегралдау қажет. Бұл теңдеулерді интегралдау негізінде жеңіл емес. Сол үшін көп жағдайда нүктелер динамикасының жалпы теоремаларын пайдаланған жөн.

Онда есепті шығару үшін, теңдеулерді интегралдамай, аталмыш теоремалардың қорытынды өрнектерін пайдаланады. Ал теңдеулерді интегралдау әрекеттері теоремаларды дәлелдеуге орындалады.

Алдымен нүктенің қозғалыс мөлшерінің қозғалыс мөлшерінің өзгеруі туралы теоремасын қарастырамыз. Ол үшін бізге күш импульсы деген түсінік қажет.