Алгебралық есептерді шешудің геометриялық әдістері

Орындаған: Сибекова А. Р.

11-сынып оқушысы

Жетекшісі: Самарбаева Б. А.

Ғылыми жұмыс

Тақырыбы:

Алгебралық есептерді шешудің геометриялық әдістері

№41 жаратылыстану-математика бағытындағы мектеп-лицей

М. Өтемісов атындағы Батыс Қазақстан мемлекеттік университетінде кеңес алу сәті

Зерттеу жұмысының өзектілігі:

Алгебралық тапсырмалардың шешімдерін табуда геометриялық түсіндірме әдісінің тиімділігі мен көрнекі шығару арқылы оңай табылатындығын көрсету.

Мақсаты

Нақты алгебралық есептерді геометриялық жолмен шешудің артықшылғын көрсету және «GeoGebra» бағдарламасын осы тақырыппен байланыстырып, тиімді қолдана білу.

Есепті геометриялық тәсілмен шығару 3 кезең арқылы жүзеге асады:

1) есептің геометриялық моделін кұру, оны геометриялық тілге келтіру;

2) пайда болған геометриялық есептің шешімі;

3) нәтижесін геометриялықтан табиғиға айналдыру.

Қозғалысқа берілген есептер

Жұмысқа берілген есептер

Тригонометриялық есептерді геометриялық әдіспен шешу

Параметрмен берілген есептерді геометриялық тәсілмен шешу

Квадрат теңдеулерге берілген есептер

Арифметикалық пррогрессия

Қысқаша көбейту формуласы

www. PresentationPro. com

Тригонометриялық есептерді геометриялық

әдіспен шешу

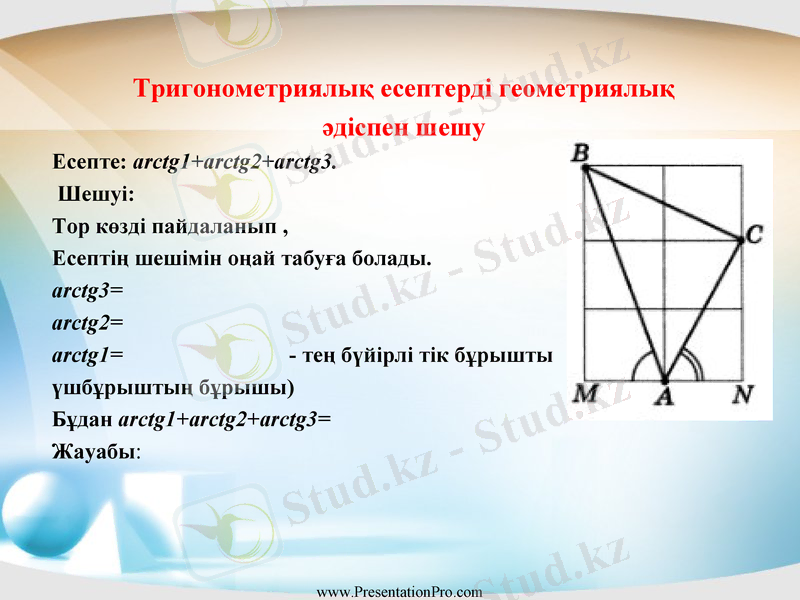
Есепте: arctg1+arctg2+arctg3.

Шешуі:

Тор көзді пайдаланып,

Есептің шешімін оңай табуға болады.

аrctg3=

аrctg2=

аrctg1= - тең бүйірлі тік бұрышты

үшбұрыштың бұрышы)

Бұдан arctg1+arctg2+arctg3=

Жауабы:

Геометриялық жолмен шешу:

Егер, онда

-ті катеттері 3 және 4, ал гипотенузасы 5 ке тең тік бұрышты үшбұрыш ретінде қарастыруға болады. Егер

болса, онда -

ке тең ұқсас үшбұрышты қарастыруға болады.

Тригонометриялық есептерді геометриялық әдіспен шешу

Шешімін тап:

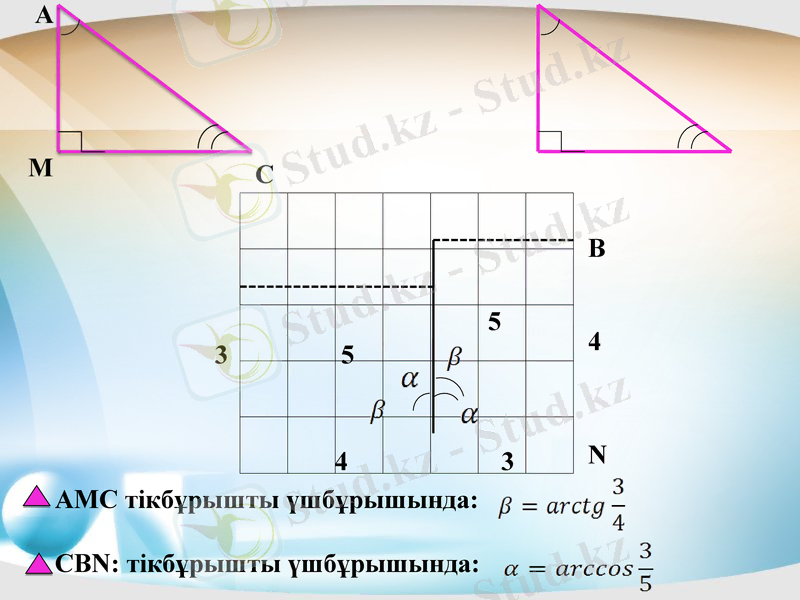
АМС тікбұрышты үшбұрышында:

СBN: тікбұрышты үшбұрышында:

, бұдан онда

Жауабы:

Параметрмен берілген есептерді геометриялық тәсілмен шешу

Теңдеулер жүйесін геометриялық тәсілмен шешу

x, y, z оң сандар деп олардың мәндерін есептемей, ху+уz өрнектің мағынасын анықтаңыз

х>0, y>0, z>0 болғандықтан, есепті геометриялық тәсілмен шешуге болады. Тік бұрышты үшбұрыштың катеттері 3 және 4 деп алып,

ху+уz=(x+z) y десек,

үшбұрыштың

ауданын екі түрлі тауып

оларды теңестіруге болады

(x+z) y=12

Жауабы:12

Арифметикалық прогрессия

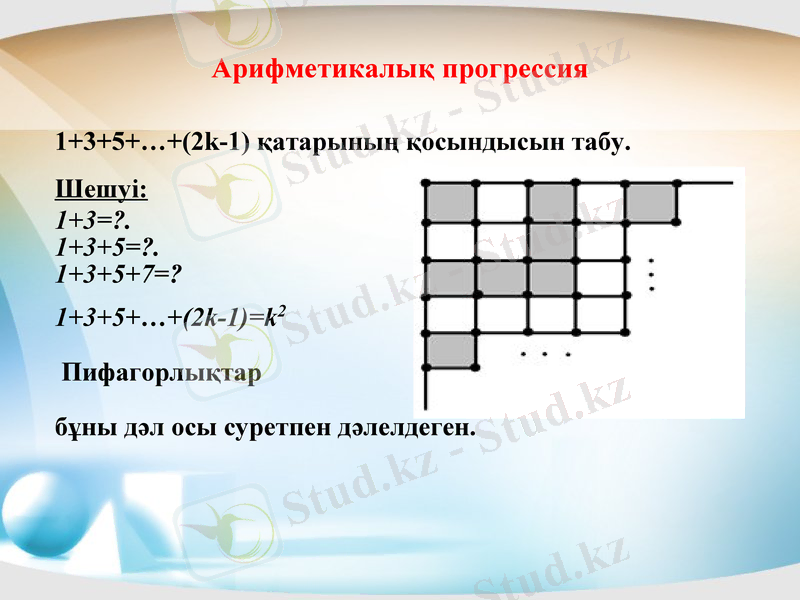
1+3+5+…+(2k-1) қатарының қосындысын табу.

Шешуі:

1+3=?.

1+3+5=?.

1+3+5+7=?

1+3+5+…+(2k-1) =k2

Пифагорлықтар

бұны дәл осы суретпен дәлелдеген.

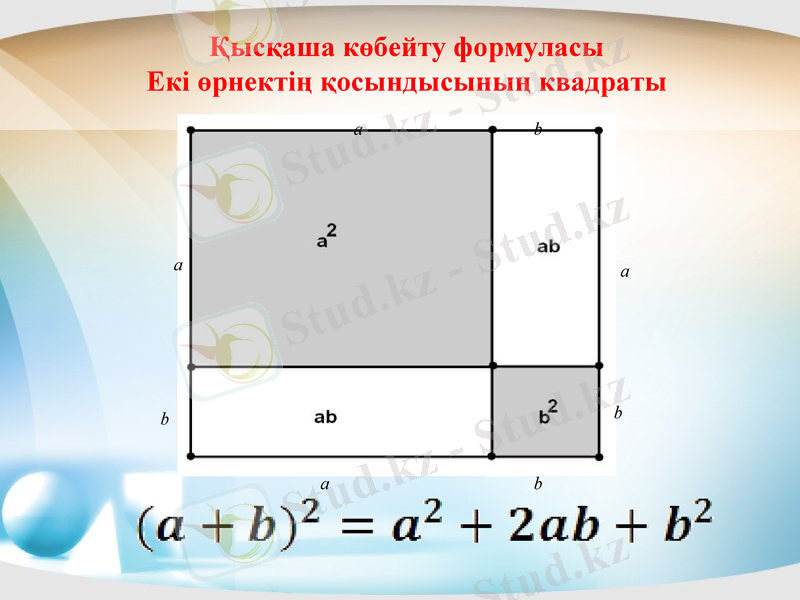
Қысқаша көбейту формуласы Екі өрнектің қосындысының квадраты

Екі өрнектің айырымасының квадраты

Екі өрнектің квадраттарының айырмасы

Қорытынды

Геометриялық әдіс дегеніміз - ол оқушыларға жақсы идея ұсынатын әдіс. Бұл жерде геометриялық заңдар мен геометриялық фигуралардың қасиеттерін пайдалана отырып, есеп шығарудың жеңіл және қызық екенін айқындайды. Сонымен, мен кейбір алгебралық есептерді геометиялық әдіспен шығарып мынадай тұжырымға келдім.

1. Әр түрлі есептерді қарастыра отырып, бірнеше геометриялық әдістерді көрсетіп, есептерді шешуде алгебралық әдіс пен геометриялық әдісті салыстырдым;

2. Жеңіл және көрнекті геометриялық әдіс пен тригонометриялық есептер шығады. Бұл әдіс есептің дұрыс шығарылу сапасын тексереді;

3. Бұл жерде геометриялық әдіс ойлау қабілетін арттырады және уақытты үнемдей білуге үйретеді. Яғни, біздерге жоғары сынып оқушыларына пайдалануға ыңғайлы. Есептердің геометриялық жолмен шығаудың артықшылықтары:

Есепті бұл жолмен шығару бастапқы іс - әрекетті нақты айқындайды;

Графиктік сурет - теңдеулерді құрастыруда, есептердің бірнеше шығару жолдарын қарастырғанда талдау жасауды жеңілдетеді;

Графиктерді қолдану аймағын кеңейтеді және графикті салу мәдениетін қалыптастырады;

Есептерді шешудің жаңа технологиясын, Geogebra программасының пайдасы көрсетеді;

Пәндер ішіндегі (алгебра мен геометрия) байланыс және пәнаралық (математика және физика) байланысты көрсетеді