Бас жиынтық және таңдама. Таңдамалы сипаттамалар

Презентация қосу

Бас жиынтық және
таңдама. Таңдамалы
сипаттамалар.

• 1.Бас жиынтық және таңдама.
• Көптеген кездейсоқ құбылыстардың
бағынатын заңдылығын анықтау
мәселесі, бақылау нәтижесінің
статистикасын зерттейтін ықтималдық
теориясының әдістеріне негізделген.
• Математикалық статистиканың
мынадай есептерін қарастырамыз:
• Жүргізілген тәжірибенің немесе
бақылаудың нәтижесінде, алынған
статистикалық мағлұматтарды жинау
және оларды топқа бөлу әдістерін
көрсету.
• Зерттеудің мақсатына байланысты
статистикалық мағлұматтарға анализ
жасау әдістерін іздеп табу.
• Математикалық статистиканың міндеті
ғылыми және практикалық тұжырымдар
жасау үшін статистикалық
мағлұматтарды жинау.
• Кейде қажетті белгісі бойынша , заттар
жиынтығындағы әрбір затты түгелдей
тексеруге тура келеді. Іс жүзінде бұлай
түгелідей тексеру өте сирек кездеседі.
• Таңдап алынған жиынтық немесе жай
ғана таңдамалы деп кездейсоқ таңдап
алынған заттардың жиынын айтады.
• Бас жиынтық деп, таңдама жасалатын
заттардың жиынтығын айтады.
• Көлем жиынтығы деп, осы жинақтың
ішіндегі заттардың санын айтады.
Мысалы, егер 1000 бөлшектен тексеру
үшін 100 бөлшек бөліп алынса, онда бас
жиынтықтың көлемі N=1000, ал
таңдамалы жиынтығының көлемі n=100
болады.
• 2. Статистикалық мәліметтерді
өндеу және көрсету тәсілі.

•
• Бақылау нәтижесінде қарастырылып
отырған белгілер жиынтықтағынан,
әрбір бірлікке қатысты сандық немесе
сапалық өзгерісі туралы мәлімет
аламыз. Статистикалық бақылаудың
мақсаты сол жиынтықта белгінің
өзгеруін (вариациясын) шешу. Ал
белгінің мүмкін мәндерін статистикада
варианта деп атайды.
• Варианталар сандық (дискретті немесе
үздіксіз) болады.
• Тәжірибе жүргізілгенде белгі мәндері
қалай болса солай орналасуы мүмкін.
Мысалы, тексерілген 100 вал диаметрі
сантиметырымен 15, 12, 16, 12, 13, 14,
16, 13, 14, 12 болып шықты. Мұны реттеп
жазсақ 12, 12, 12, 13, 13, 14, 14, 15, 16,
16 болар еді. Мұны ықшамдап кесте
түрінде жазсақ, мынадай болады:
•
• 1- кесте
Xi 12 13 14 15 16 ²
ni 3 2 2 1 2 10
• Бұл кестенің жоғарғы жолында белгі
мәндері (варианталары), ал төменгі
жолында әрбір мәнінің неше рет
кездескені келтірілген. Осылай реттелген
кестені вариациялық қатар деп атайды.
• Әдетте белгіні (вариантаны) кездейсоқ
шамалар сияқты Х, У,.. әріптерімен
белгілеп,оның қабылдайтын мәндерін
(варианталарды)

х1 , х2 ,...., хк ; у 1 , у 2 ,...., ук;
• арқылы белгілейміз.
• Варианта қайталап отыруы
мүмкін. Ол қайталаулардың
абсолютті санын (жиілігін) n1, n2…
nk деп белгілесек, онда
вариациялық қатардың жалпы
түрін мына кесте көрсетеді:
Xᵢ X₁ X₂ ….. Xk Σ
• 2 – кесте
nᵢ n₁ n₂ …… nk n
• Мұнда, хі – варианталары;
• ni – жиіліктер;

• Іс жүзінде варианта абсолютті
жиілікпен қатар салыстырмалы
жиілік түрінде де беріледі. Бұл
жағдайда екінші кесте былай
жазылады:
• 3 –Xᵢкесте
X₁ X₂ ….. Xk Σ

Wᵢ W₁ W₂ …… Wk 1
ni
• Мұндағы wi салыстырмалы жиілік
n
• n ni вариация қатардың көлемі.
• wi 1 салыстырмалы жиіліктердің
қосындысы тең бірге.

• Егер варианталар үздіксіз өзгеретін болса, онда
вариациялық қатарды интервал бойынша құруға
тура келеді.
• Жалпы түрде интервалдық қатар мынадай
болады:
•
• 4 – кесте. Жиіліктің интервалдық түрі:
•
X (X2;X3) (X3;X4) …..
(X1;X2) (Xm;Xm+1)

ni n1 n2 n3 ….. nm
• немесе
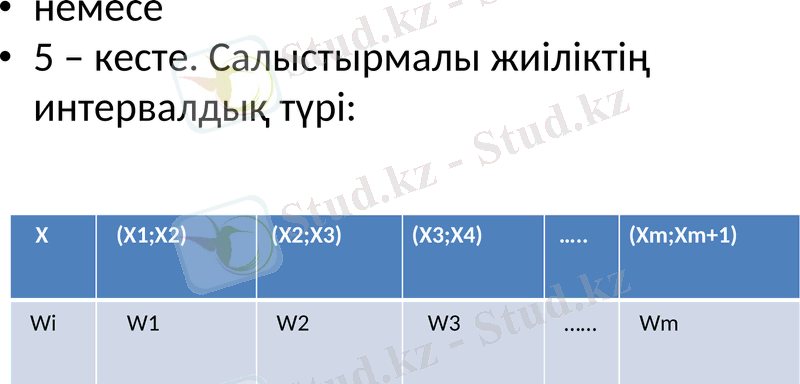
• 5 – кесте. Салыстырмалы жиіліктің
интервалдық түрі:

X (X1;X2) (X2;X3) (X3;X4) ….. (Xm;Xm+1)

Wi W1 W2 W3 Wm
……
• Мұндағы (x1;x2), (x2;x3), (x3;x4) ...,
(xm;xm+1) аралықтары белгінің
мүмкін мәндері жататын
интервалдар. к1= x2-x1; к2= x3-
x2,....., кm= xm+1-xm – айырымдары
интервал узындығын сипаттайды.
• Полигон және гистограмма.
• Жиілік полигоны деп (xі; ni), (x2;
n2), ..., (xк; nк), нүктелерін
кесінділермен қосқанда шыққан
сынық сызықтарды айтады.
• Полигон салу үшін абсцисса осіне x і –
варианттары, ал оларға сәйкес жиіліктері
ордината осіне салынады. (xі; ni) нүктелерін
кесінділермен қоссақ жиілік полигонын аламыз .
• Салыстырмалы жиілік полигоны деп (x1; w1),
(x2; w2), ..., (xк; wк) нүктелерін кесінділермен
қосқанда шыққан сынық сызықтарды айтады.
• Салыстырмалы жиілік полигонын салу үшін,
абсцисса осіне xі – варианттары, ал оларға
сәйкес wi – салыстырмалы жиіліктер ордината
осіне салынады.
• (xі; wі) – нүктелерін кесінділермен қоссақ
салыстырмалы жиілік полигонын аламыз.
• Жиілік гистограммасы деп
табандарының ұзындықтары һ – қа
ni
тең дербес интервалдан, ал
h
биіктері қатынасындай болатын
тік төртбұрыштардан құрылған
сатылы фигураны айтады.
• Жиілік гистограммасын салу
үшін абсцисса осіне дербес
интервалды, алn олардың
i
жоғарғы
жағынан абсцисса
h осіне
паралелль және одан ара
қашықтықтары - қа тең
ni
• Мұндағы -h жиілік
тығыздығы. Жиілік
гистограммасының ауданы барлық
ni
h

жиіліктердің қосындысына тең,
яғни таңдау көлеміне тең.
• Салыстырмалы жиілік
w
гистограммасыh
i
деп,
табандарының ұзындықтары һ – қа
тең интервалдар, ал биіктіктері
(салыстырмалы жиілік
тығыздығы) қатынасына тең тік
төртбұрыштардан құрылған
• Салыстырмалы жиілік гистограммасын салу үшін абсцисса осіне
интервалдарды, ал оның жоғарғы жағынан абсцисса осіне
паралелль және одан
wi
• қашықтықтары
h

қатынасына тең кесінділерді саламыз.
• і – ші тік төртбұрыштың ауданы:
wi
h w i
• h - ге тең.

• Сонымен салыстырмалы жиілік гистограммасының ауданы,
барлық салыстырмалы жиіліктер қосындысына, яғни бірге тең.

•
• 3.Таңдамалы сипаттамалар.
•
• Статистикалық үлестірімнің сандық
сипаттамалары мен оларды есептеу
формулаларын қарастырайық.
• Арифметикалық таңдамалы орта.
Белгінің (Х) арифметикалық ортасы деп
варианталардың жалпы санын
таңдаманың көлеміне қатынасын
айтады, яғни (егер барлық варианталар
әртүрлі болса):
k

• жай түрі
x
i 1
i
хт
• n

• Мұнда, х i
•
• варианталар (белгі) мәндері:
к
• n ni - таңдама көлемі.
i 1
• Егер таңдама вариациялық қатармен берілсе,
онда
•
Xᵢ X₁ X₂ …… Xk

nᵢ n₁ n₂ ……. n
•
k
•
n i xi
•
x т i 1
n
• өлшенген түрі
•
•
• Мұнда,

• nі – варианталар cалмағы (жиілігі);
•
•

n ni
- таңдама көлемі;

• хі – варианталар.
•
• Мода (М0). Берілген вариациялық қатардың
ең жиі кездесетін вариантасын мода деп
атайды. Басқаша айтқанда, ең жоғары
жиілікке сәйкес варианта мәні мода болады.
• Медиана (Ме). Жиынтықты тең етіп екіге
бөлетін белгі мәнін медиана деп атаймыз.
Егер белгінің өзгеруші мәндері тақ болып,
ұлғаю ретімен орналасса x1,x2, ..., xm-1, ,xm
,xm+1, ..., ,x2n-1, онда бұл үйлестіру үшін Ме
медианасы хm вариантасына тең, яғни Ме
=хm, өйткені Ме =хm – нен төмен де жоғары
да белгінің саны бірдей m-1 мәндері
орналасқан.
• Ал варианта саны жұп болса, x1,x2,
..., xm-1, ,xm ,xm+1, ..., ,x2m, онда бұл
жиынтықты тең екіге бөлетін
медиана мәні (xm ,xm+1)
аралығында болады. Бұл
жағдайда медиана Ме – нің мәні
x m x m 1
осы екі вариантаның
Me
арифметикалық ортасы 2 болады,
яғни
•
• Вариация құлашы.

• Ауытқу сипаттамаларының
ішіндегі ең қарапайым түрі –
вариация құлашы. Мұның мәні
варианталарының максимум және
минимум мәндерінің айырымына
тең: R x x
max min
• Дисперсия және орташа
квадраттық ауытқу.
• Анықтама.
• Кездейсоқ шамамен оның
математикалық күтімі айырымының
квадратының математикалық күтімін
дисперсия (шашырау дейді).
• Х кездейсоқ шамасының
дисперсиясын Д(Х) арқылы
белгілесек,Dонда
( Х ) анықтама 2
M X M бойынша:
(X )
• Белгі мәндерінің арифметикалық
ортадан ауытқу квадраттары
қосындысының арифметикалық
ортасын таңдамалы дисперсия
немесе дисперсия дейміз. 2

• n (x х )
- өлшенген түрі,
2 i i т
D
T
n

DT 2 i
( x xт )
• немесе n
• - жай түрі
• Түзетілген дисперсия
2 n
s Д Т
n 1
•
• Орташа
Тквадраттық
ДТ ауытқу

•
т
V коэффициенті
• Вариация 100%
xт
• Тандама ортаны және дисперсияны есептеу
көбейту әдісі.
• а) Шарттық варианталар.
• Делік, таңдама варианттарлары өспелі ретінде
орналасқан, яғни вариациялық қатар түрінде.
• Айырымы h – қа тең арифметикалық прогрессияны
құрастыратын варианталарды бірдей қашықтықтағы
x C деп атайды.
варианталар
uі i
• h
•
• формуламен анықталатын вариантталарды
• шарттық варианта деп атайды.
• Мұндағы С – жалған ноль (санақтың жаңа бастамасы).
• Һ – қадам (екі көрші варианталардың
айырмасы).
• б) Таңдамалы орта мен дисперсияны
есептеу көбейту әдісін қарастырайық.
• Делік, таңдама бірдей қашықтықтағы
варианталар және оларға сәйкес
жиіліктер түрінде берілсін. Бұл
жағдайда таңдамалы ортаны және
дисперсияны көбейту әдісі
формулаларымен табу қолайлы.
• Яғни, xT M *1 h C -таңдамалы орта
• * - таңдамалы
DT M 2 ( M 1 ) h 2
* 2

• дисперсия
• Мұндағы һ – қадам
• С – жалған ноль (ең үлкен
жиілігі бар варианта).
• * n i u i
M1
• n бірінші ретті шарттық сәт.

• M n n u
*
i i

• екінші ретті шарттық сәт.
• Көбейтінді әдісін қолданауын бір
мысалда қарастырайық.
•
• Мысал. Көлемі n=100 берілген
үлестірімнің таңдамалы орта мен
дисперсиясын табыңыз.

Xᵢ 12 14 16 18 20 22
nᵢ 5 15 50 16 10 4
• Шешуі.
• Бірінші есептеу кестені құрамыз; Ол үшін:
• 1.Варианталарды бірінші бағанға жазамыз.
• 2.Жиіліктерді екінші бағанға жазамыз,
жиілік қосындысын (n=100) екінші
бағанның төменгі торшасына жазамыз.
• 3.Жалған ноль (С) ретінде С=16
вариантаны аламыз, оның ең үлкен жиілігі
бар (С ретінде бағаның ортасында тұрған
әлде қандай болса вариантаны алуға
болады).
• Жалған ноль тұрған жолдың
үшінші бағанның торшасына 0
жазамыз, оның үстінен тізбектеп –
(-1), (-2) – жазамыз, ал 0 – дың
астына 1,2,3 жазамыз.
n i u i
• 4.Жиіліктердің шарттық
варианталарға
n i u i
• көбейтінділерін төртінші
бағанға жазамыз, ал олардың
қосындысын

• бағанның төменгі торшасына
Xᵢ nᵢ uᵢ nᵢ*uᵢ nᵢ*uᵢ² nᵢ(uᵢ+1)² (uᵢ+1)²
12 5 -2 -10 20 5 1
14 15 -1 -15 15 0 0
16 50 0 0 0 50 1
18 16 1 16 16 64 4
20 10 2 20 40 90 9
22 4 3 12 36 64 16
Σ 100 Σnᵢ*uᵢ²=127 Σnᵢ(uᵢ+1)²=
Σnᵢ*uᵢ=23 273
• Бақылау:
• n i ( u i 1) ni ui 2 ni ui n
2 2

• 273=127+2*23+100
• 273=127+146
• 273=273
• 5) Жиілікті шарттық
варианталардың квадраттарына
n i u i
көбейтіп шыққан көбейтінділерді
бесінші бағанға жазамыз,
n u
i i
шыққан сандарды қосып,
олардың қосындысын
• бағанның төменгі торшасына
орналастырады.
• 6)Шарттық ықтималдылықтарды 1
санына үлкейтіп және олардың
квадраттарын сәйкес жиіліктерге
көбейтіп n i ( u i 1) 2
• көбейтіндіні алтыншы бақылау
бағанға жазамыз; барлық шыққан
сандарды қосып, олардың 2
қосындысын
n i ( u i 1)

• бағанның төменгі торшасына
орналастырамыз.
• Қорытындыда 1-ші кесте шығады.
• Бақылау үшін мына теңбе-теңдікті
қолданамыз:
n i ( u i 1) 2
ni ui 2 ni ui n
• 2
• Бақылау: n i ( u i 1 ) 273
ni u i 2 ni ui n

• =127+2*23+100
• Бақылау қосындылардың дәл келу
есептеуінің дұрыс болу куәлігі.
• . Бірінші және екінші ретті
шарттық сәттерді есептейміз.
ni u i 23
M 1* 0,23
n 100

ni ui2 127
M
2 1,27
n 100

• Қадамын табайық һ=14 – 12=2
• Жалған ноль С=16 еске алып,
таңдамалы орта мен дисперсияны
есептейміз.
•
x t M 1 h C 0 , 23 2 16 16 , 46
•

2 1

DT M (M ) h 1.27 0.23 2 4.87
* * 2 2

T DT 4,87 2,21

Ұқсас жұмыстар

Жағдайдың статистикалық сипаттамалары

Вариациялық қатар

Статистикалық болжамдарды тексеру

Дисперсиялық талдау

БАҚЫЛАУ ІШІНАРА

Оралымды алгоритмдер

Жеке фактордың белгінің жалпы өзгергіштігіне тигізетін үлесін дисперсиялық талдау арқылы анықтау

Экономикалық көрсеткіштерді есептеу

Ақпараттарды өңдеу әдісі және оның нәтижелерін талдау

КОРРЕЛЯЦИЯ КОЭФФИЦИЕНТІН ЭКОНОМИКАЛЫҚ ҚҰБЫЛЫСТАРДЫ ЗЕРТТЕУДЕ ПАЙДАЛАНУ

Пәндер