Гетероскедастиканы анықтау және түзету: Голдфельд-Квандт тесті мен жалпыланған ең кіші квадраттар әдісінің қолданбалы мысалы



Гетероскедастикалық. Гетероскедастикалықты анықтау тесттері

1. маңызы және оның салдары.
Ең кіші квадраттар әдісінің алғы шарттарының бірі кездейсоқ ауытқудың тұрақтылық дисперсиясы: кез келген і және j бақылаулары үшін:

Осындай жағдайлардың пайда болуы гомоскедастикалық (дисперсия ауытқуының тұрақтылығы) деп аталады.
Ал керісінше жағдайда оны гетероскедастикалық (дисперсия ауытқуының тұрақсыздығы) деп атайды.
бар болуын көрнек түрде корелляция өрісінен көруге болады .
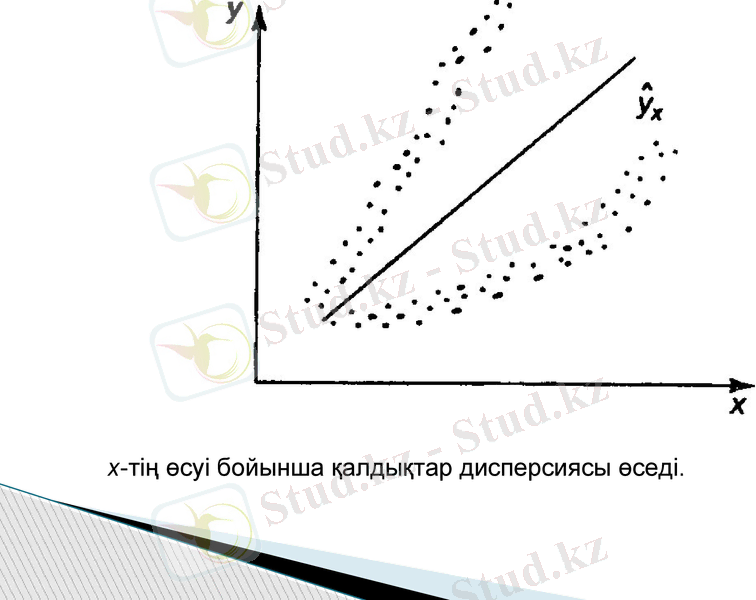
х-тің өсуі бойынша қалдықтар дисперсиясы өседі.
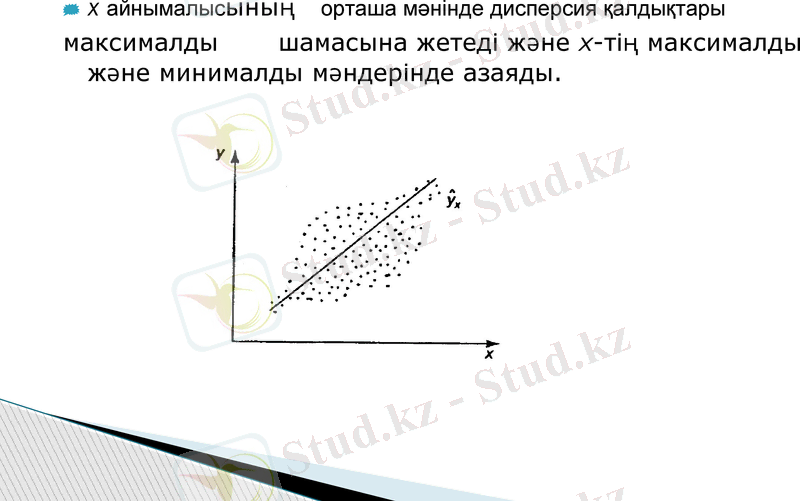
х айнымалысының орташа мәнінде дисперсия қалдықтары
максималды шамасына жетеді және х-тің максималды және минималды мәндерінде азаяды.
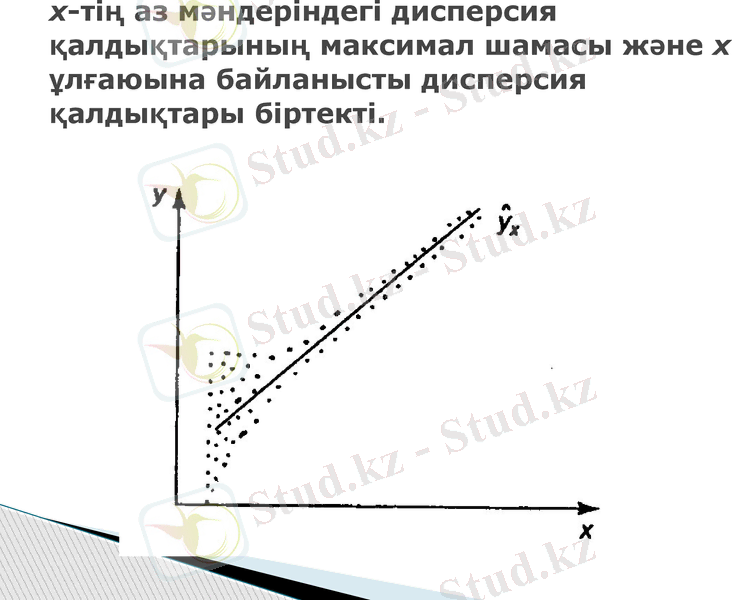
х-тің аз мәндеріндегі дисперсия қалдықтарының максимал шамасы және х ұлғаюына байланысты дисперсия қалдықтары біртекті.

салдары:
регрессия теңдеуінің параметрлерін бағалау эффективті емес болады;
регрессия параметрлерінің стандартты қателеріне баға беру бұрыс болып шығады.

2. Гетероскедастикалықты байқау.
Ең көп тарағаны Голдфельд-Квандт тесті болып табылады.
Бұл тест келесі түрін тексеруге қолданылады: егер орташа квадраттық ауытқуы кездейсоқ і бақылауындағы хі белгі - факторына пропорционал болса.
Бұл жағдайда кездейсоқ жиынтығы нормальды үлестірілген деп болжау жасалады.

Голдфельд-Квандт алгоритм - тесті төменде келтірілген.
Барлық бақылаулар хі мәндері бойынша реттеледі.
Бірінші п/ (1; n) бақылаулар үшін
регрессия бағаланады.
Ақырғы п/ бақылаулар үшін
регрессия бағаланады.

Белгі - нәтиже мәні фактілік квадраттар сомасының ауытқуынан және оның екі регрессиясы үшін де есеп айыру мәндерімен есептеледі:
және

Ауытқу квадраттар сомасының қатынасы есептелінеді: алымында ауытқу квадраттар сомасының көбірегі болу керек. Бұл қатынас Ғ үлестіруіне ие болады,
және еркіндік дәрежелерімен,
к1=к2, мұнда h - регрессия теңдеуіндегі бағаланатын параметрлерінің саны.

Егер Ғбақылау,
онда орны болады.
Егер модельде бірден көбірек факторлар болса, онда бақылаулар сол факторлардан лайықты реттелуі керек, қайсысы қалай болжамданғандай, -мен тығыз байланысқан және n/ h-тан үлкен болу керек.

Мысал. 20 зерттеу бойынша азық-түлікке у (бірлік ақша) моделі құрылған
у=20, 84+0, 44 х-тың әр мәнінде қалдықтар шамалары мынадай болады:
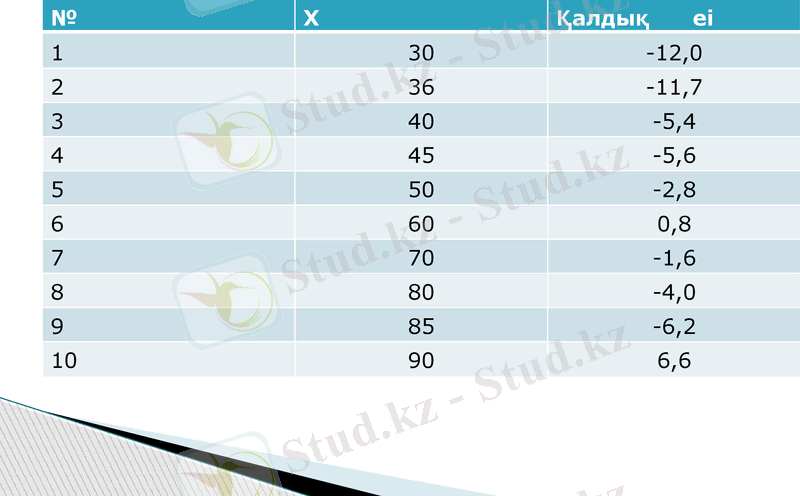
№
X
Қалдық еi
1
30
-12, 0
2
36
-11, 7
3
40
-5, 4
4
45
-5, 6
5
50
-2, 8
6
60
0, 8
7
70
-1, 6
8
80
-4, 0
9
85
-6, 2
10
90
6, 6
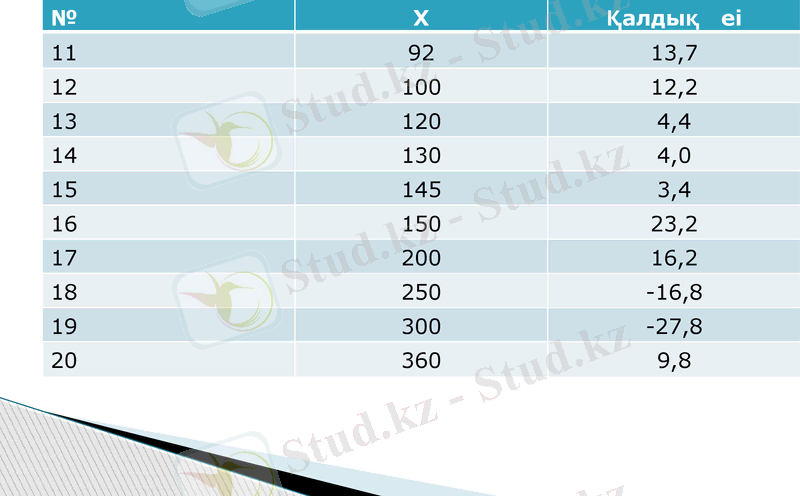
№
Х
Қалдық еi
11
92
13, 7
12
100
12, 2
13
120
4, 4
14
130
4, 0
15
145
3, 4
16
150
23, 2
17
200
16, 2
18
250
-16, 8
19
300
-27, 8
20
360
9, 8

1. Х айнымалының мәніне байланысты қалдықтар графигін салыңыз және шешімдер жасаңыз.
2. Гетероскедастиканы анықтау үшін Гольдфельд - Квандт тестін қолданыңыз.
3. Жалпыланған ең кіші квадраттар әдісін пайдаланып, модельді жақсартыңыз.
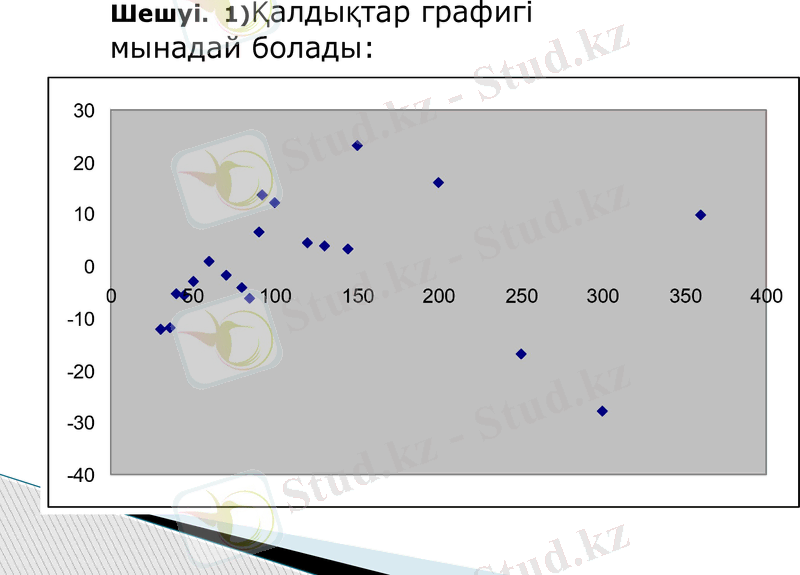
Шешуі. 1) Қалдықтар графигі мынадай болады:

Әртүрлі х-тің мәндерінде қалдықтар тербелесі бірдей еместігін графигі көрсетеді:
егер х<90 болса, онда e< 0;
ал егер х (90; 200) аралықта жатса, онда e>0.
Егер х>200 үлкен болса, е-нің өзгеру аралығы, х-тің кіші мәндеріне қарағанда, одан да көп.
Сонымен, график арқылы қалдықтардың барын болжауға болады.

2) Гольдфельд-Квандт тестін қолдану үшін у жөнінде ақпараттар қажет.
Бұл ақпараттар берілмесе де, оларды табуға болады.
Регрессия теңдеуі негізінде есептеуші мәндерін табамыз.
Енді фактілік мәндерін табамыз.
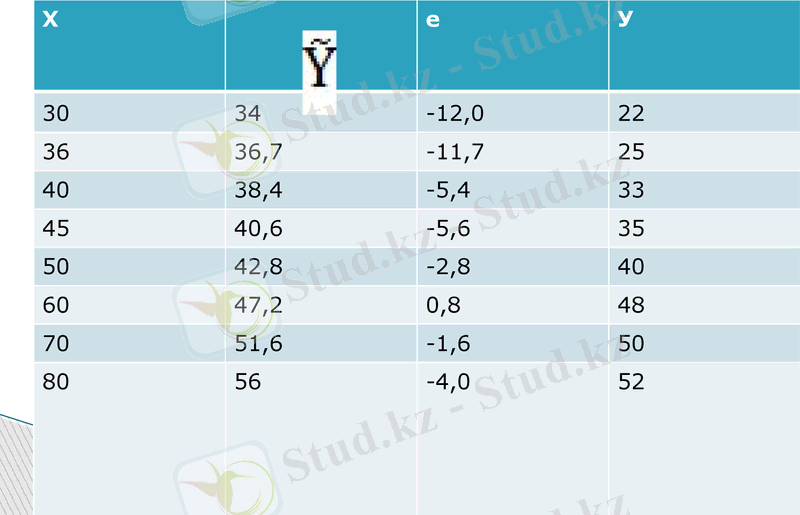
Х
е
У
30
34
-12, 0
22
36
36, 7
-11, 7
25
40
38, 4
-5, 4
33
45
40, 6
-5, 6
35
50
42, 8
-2, 8
40
60
47, 2
0, 8
48
70
51, 6
-1, 6
50
80
56
-4, 0
52
85
58, 2
-6, 2
52
90
60, 4
6, 6
67
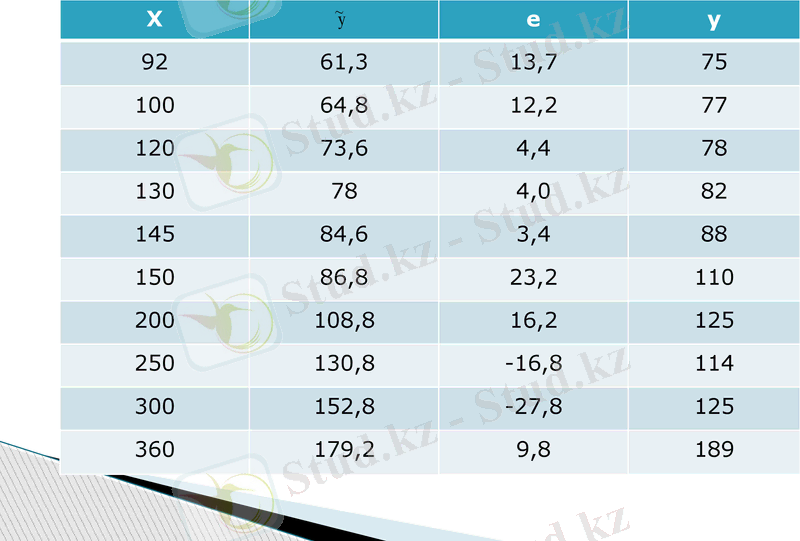
X
e
y
92
61, 3
13, 7
75
100
64, 8
12, 2
77
120
73, 6
4, 4
78
130
78
4, 0
82
145
84, 6
3, 4
88
150
86, 8
23, 2
110
200
108, 8
16, 2
125
250
130, 8
-16, 8
114
300
152, 8
-27, 8
125
360
179, 2
9, 8
189

Орталық С бақылауларды кестеден шығарайық. Жиынтықты екі бөлікке бөлеміз: а) бір бөлігінде х мәндері орта мәндерінен төмен; б) екінші бөлігінде - х мәндері орта мәндерінен жоғары.
С=4 болсын, бұл бақылаулар мынадай реттік нөмірлерімен: 9, 10, 11, 12. Онда әр бөлікте 8 бақылаулардан қалады. Әр бөліктін регрессия теңдеуін табамыз.
Бірінші бөлігін қарастырамыз және оған есептеуші кестені құрамыз.
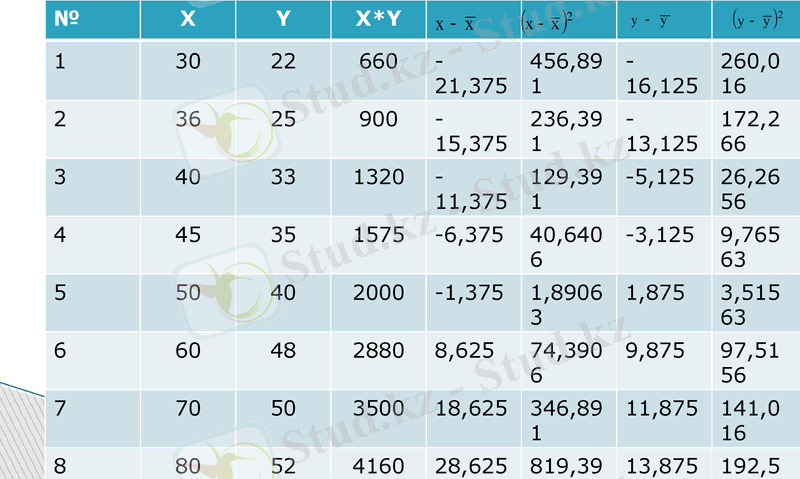
№
X
Y
X*Y
1
30
22
660
-21, 375
456, 891
-16, 125
260, 016
2
36
25
900
-15, 375
236, 391
-13, 125
172, 266
3
40
33
1320
-11, 375
129, 391
-5, 125
26, 2656
4
45
35
1575
-6, 375
40, 6406
-3, 125
9, 76563
5
50
40
2000
-1, 375
1, 89063
1, 875
3, 51563
6
60
48
2880
8, 625
74, 3906
9, 875
97, 5156
7
70
50
3500
18, 625
346, 891
11, 875
141, 016
8
80
52
4160
28, 625
819, 391
13, 875
192, 516
Σ
411
305
16995
2105, 88
902, 875

Қажетті мәндерін табамыз:
Онда
,
,
,

Сонда, мынадай теңдеу шығады
Осыған ұқсас, екінші бөлігіне кесте құрамыз:
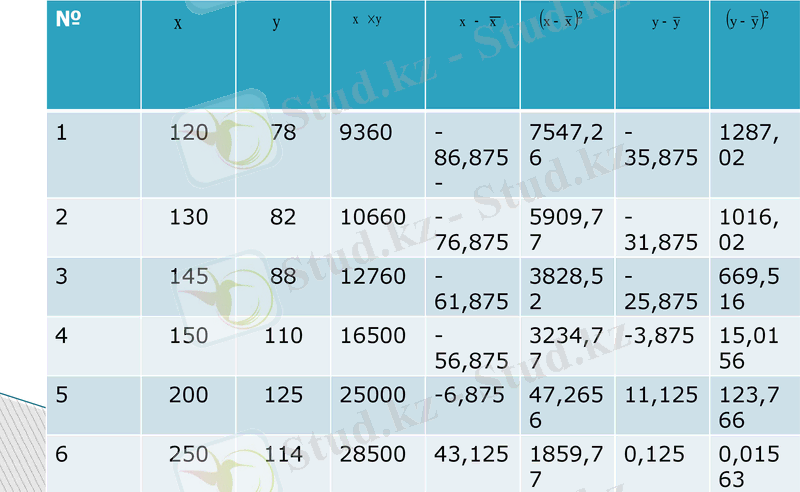
№
1
120
78
9360
-86, 875-
7547, 26
-35, 875
1287, 02
2
130
82
10660
-76, 875
5909, 77
-31, 875
1016, 02
3
145
88
12760
-61, 875
3828, 52
-25, 875
669, 516
4
150
110
16500
-56, 875
3234, 77
-3, 875
15, 0156
5
200
125
25000
-6, 875
47, 2656
11, 125
123, 766
6
250
114
28500
43, 125
1859, 77
0, 125
0, 01563
7
300
125
37500
93, 125
8672, 27
11, 125
123, 766
8
360
189
68040
153, 125
23447, 3
75, 125
5643, 77
Σ
1655
911
208320
54546, 9
8878, 88

Қажетті мәндерін табамыз:
Онда
,
,
,
,
,

Сонда, мынадай теңдеуді аламыз
Енді әр топқа: у-тін теоретикалық мәндерін, қалдықтар е-ні және оның квадраттарын е2 анықтаймыз.
.
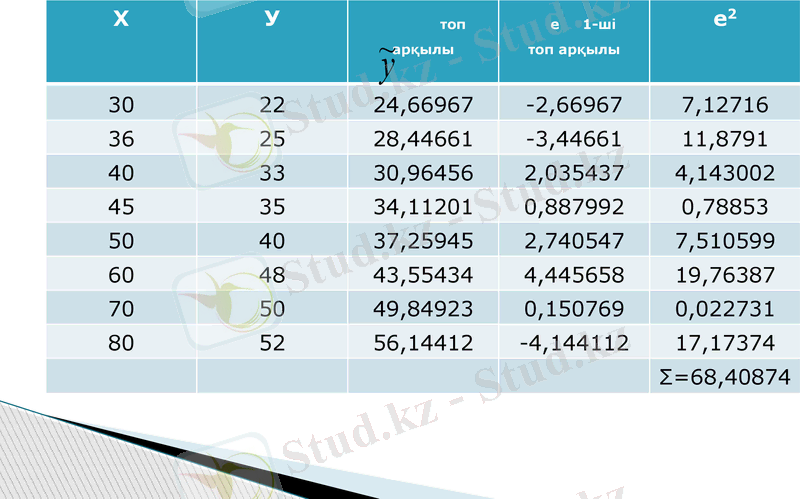
Х
У
топ арқылы
е 1-ші топ арқылы
е2
30
22
24, 66967
-2, 66967
7, 12716
36
25
28, 44661
-3, 44661
11, 8791
40
33
30, 96456
2, 035437
4, 143002
45
35
34, 11201
0, 887992
0, 78853
50
40
37, 25945
2, 740547
7, 510599
60
48
43, 55434
4, 445658
19, 76387
70
50
49, 84923
0, 150769
0, 022731
80
52
56, 14412
-4, 144112
17, 17374
Σ=68, 40874
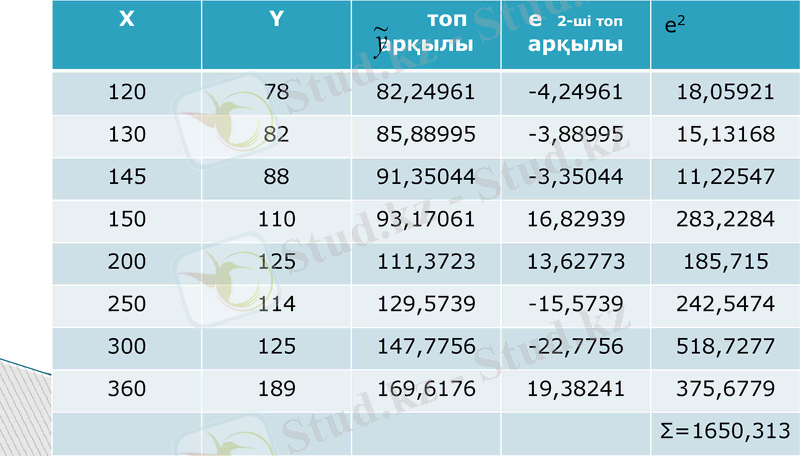
X
Y
топ арқылы
е 2-ші топ арқылы
120
78
82, 24961
-4, 24961
18, 05921
130
82
85, 88995
-3, 88995
15, 13168
145
88
91, 35044
-3, 35044
11, 22547
150
110
93, 17061
16, 82939
283, 2284
200
125
111, 3723
13, 62773
185, 715
250
114
129, 5739
-15, 5739
242, 5474
300
125
147, 7756
-22, 7756
518, 7277
360
189
169, 6176
19, 38241
375, 6779
Σ=1650, 313
е2

Енді қалдықтар квадраттарының ең үлкен соммасының кіші соммасына қатынасын
табамыз:
5% маңыздылық деңгейінде және дәреже еркіндік санында 8-2=6 (өйткені әр топта 8 элементтен бар) осы шаманы (Ғ фактолықты) Ғ-критериінің кестелік мәнімен салыстырамыз:

Сонымен Ғфакт>Ғкриз, бұдан мына қорытындыға келеміз: қалдықтардың гетероскедастикалығы бар.
Қалдықтардың гетероскедастикалығын төмендету үшін жалпыланған ең кіші квадраттар әдісін қолдануға болады. Ол үшін есептеуші кесте құрамыз.
.
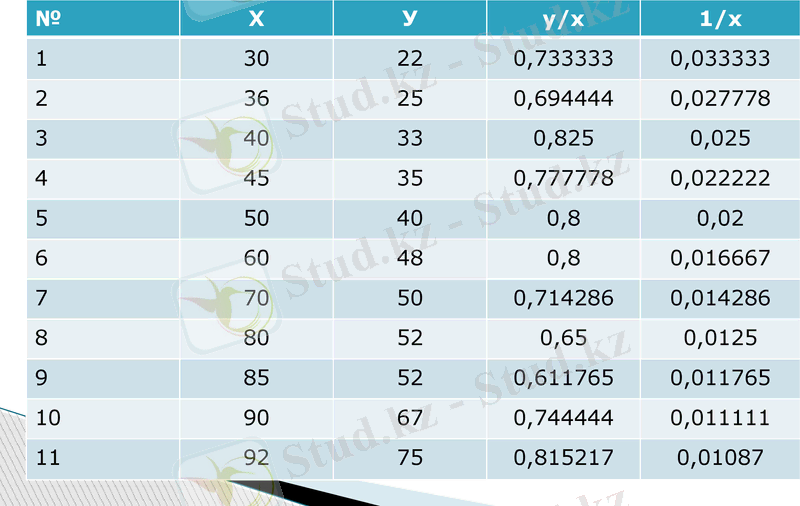
№
Х
У
y/x
1/x
1
30
22
0, 7
0, 0
2
36
25
0, 69
0, 027778
3
40
33
0, 825
0, 025
4
45
35
0, 8
0, 0
5
50
40
0, 8
0, 02
6
60
48
0, 8
0, 016667
7
70
50
0, 714286
0, 014286
8
80
52
0, 65
0, 0125
9
85
52
0, 611765
0, 011765
10
90
67
0, 7
0, 0
11
92
75
0, 815217
0, 01087
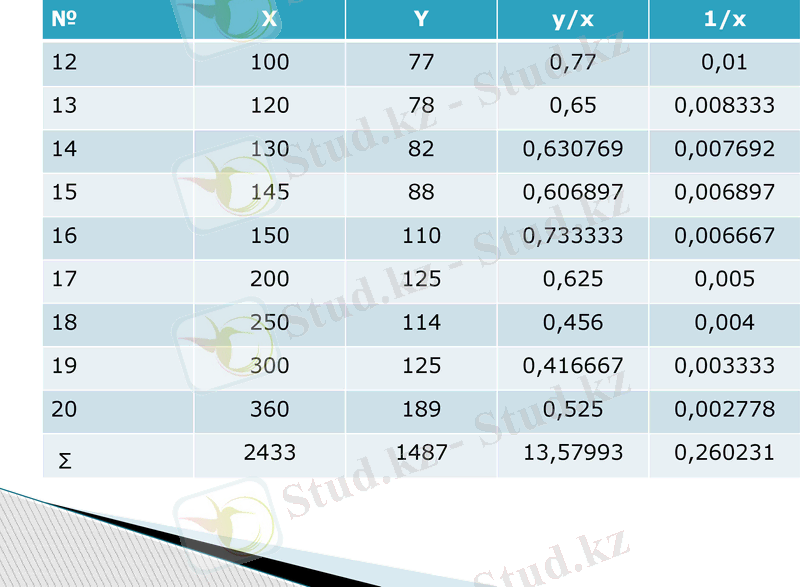
№
X
Y
y/x
1/x
12
100
77
0, 77
0, 01
13
120
78
0, 65
0, 008333
14
130
82
0, 630769
0, 007692
15
145
88
0, 606897
0, 006897
16
150
110
0, 7
0, 006667
17
200
125
0, 625
0, 005
18
250
114
0, 456
0, 004
19
300
125
0, 416667
0, 00
20
360
189
0, 525
0, 002778
2433
1487
13, 57993
0, 260231
Σ

Нормальдық теңдеулер жүйесі мұнадай болады:
Онда болады:
Теңдеулер жүйесін Крамер әдісімен шығарамыз.

Онда болады :
Осыдан шығады :
.

Осыдан шыққан теңдеуінде
гетероскедастикалылық жойылған.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz