Жиынтық сызықтық регрессия моделі

Жиынтық сызықтық регрессия моделі .

1. Жиынтық регрессияның қалыпты классикалық сызықты моделі.

Көпфакторлық регрессия теңдеуінің жалпы түрі мынадай болады:

(1)

мұндағы k - факторлық белгілер саны.

Нәтижелі белгі у-тің екі факторлық белгілерден сызықты моделінің тәуелсіздігін қарастырайық.

Ол модельдің түрі мынадай

Параметрлер а, в1 және в2 табу үшін нормальдық теңдеулер жүйені шешеміз:

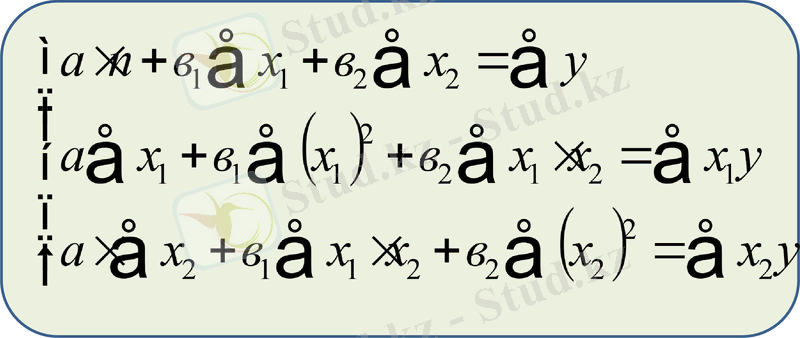
2. Жиынтық регрессияның сызықтық моделінің параметрлерін бағалау.

Жиынтық корреляция теңдеулер жүйесін ықшамдау үшін, (1) бірінші теңдуінің параметрлерін есептеуіне қажетті болатын, барлық белгілердің жеке мағыналарынаң осы белгілерден орта шамалардан ауытқуын енгізейік

Онда жиынтық регрессияның k теңдеулер жүйесін аламыз:

Осы жүйені шығарып, регрессия коэффиценттерінің мәндерін табамыз.

Теңдеудің бос мүшесі төменде келтірілген формула арқылы табылады:

3. Жиынтық және дербес корреляция.

Көп факторлық жүйе әр түрлі маңызды және әр түрлі қолдануы болатын байланыс тығыздығының көрсеткіштер жиынын талап етеді.

Факторлық белгілер байланысының өлшеу негізі қос корреляция коэффиценттерінің матрицасы болады.

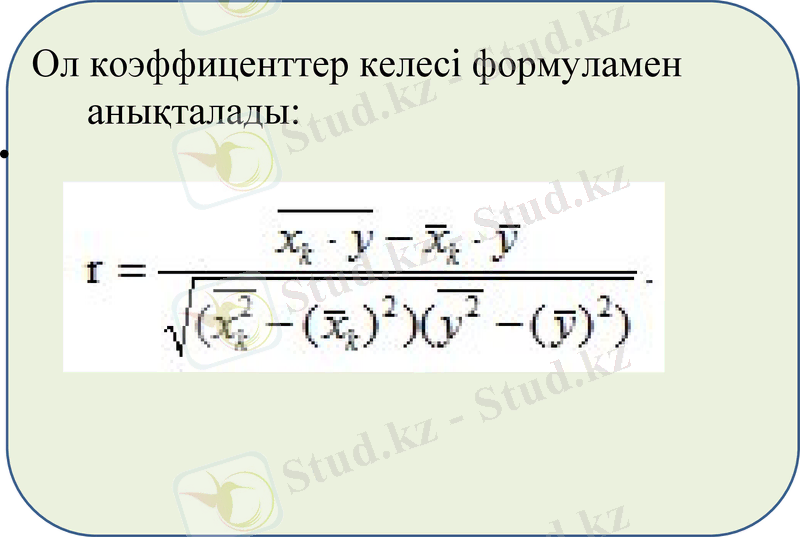
Ол коэффиценттер келесі формуламен анықталады:

Корреляцияның қос коэффиценттер негізінде, теңдеуге кіретін барлық факторлардың қорытынды нәтижелік белгімен байланыстары, ең ортақ тығыздық көрсеткіші есептелінеді - детерминацияның R² жиынтық коэффиценті, келесі формула бойынша :

Мұндағы:

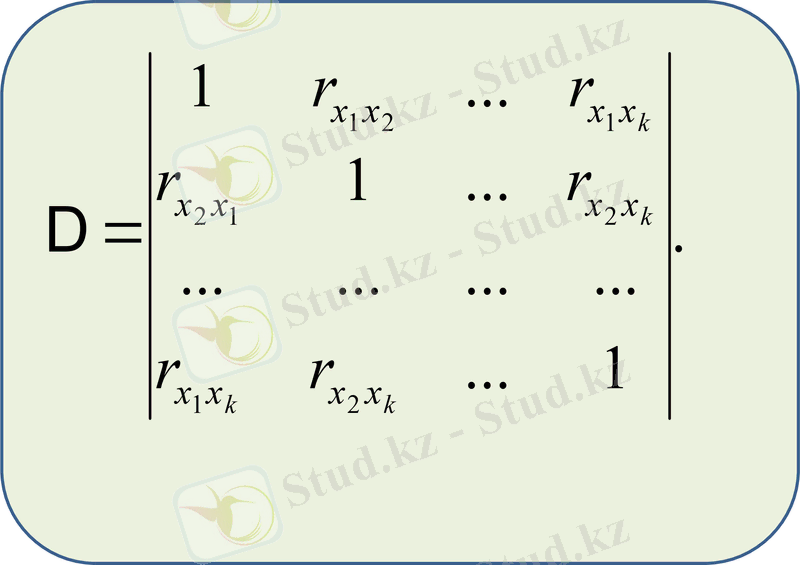
Егер жиынтық жүздік және мыңдық бірліктерден құрылса, бұл тәсілмен нәтижелі белгінің есептеуіш мәндерін есептемей детерминация коэффицентін анықтауға болады.

Егер жиынтық үлкен болмаса, жиынтық регрессия теңдеуінде қарастырылған факторлық және нәтижелік белгілер арасындағы байланыстың адекваттылығын анықтау үшін, сызықты емес корреляциядағыдай корреляция индексін қолдануға болады.

Корреляция индексі келесі формула

бойынша табылады:

Екі факторлық регрессия теңдеуінің тығыздық байланысын корреляцияның қосақты коэффициенттері анықтайды. Оларды және келесі формулалар бойынша есептейміз :

Мұндағы

Бұл есептеулерден кейін, жиынтық корреляцияның коэффициентін табамыз:

Бұл коэффициенттің мәндері (0; 1) аралықта жатады.

Жиынтық корреляцияның

коэффициенті көрсеткіш у-тің бір мезгілде х1, х2 факторлармен байланыс тығыздығын бағалайды.

Нәтижелі белгімен бір факторлық арасындағы байланыс тығыздығы

дербес корреляция және

коэффициенттерімен сипатталады,

яғни

және

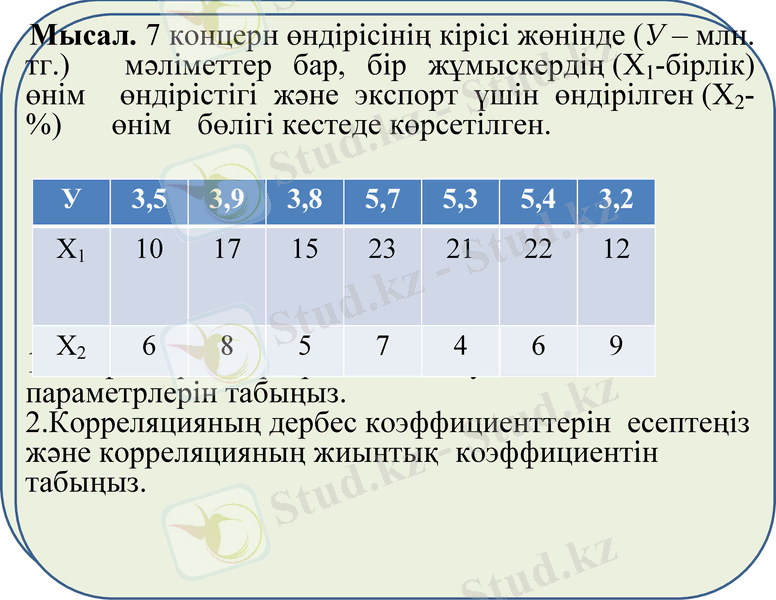
Мысал. 7 концерн өндірісінің кірісі жөнінде (У - млн. тг. ) мәліметтер бар, бір жұмыскердің (Х1-бірлік) өнім өндірістігі және экспорт үшін өндірілген (Х2- %) өнім бөлігі кестеде көрсетілген.

1. Екі факторлық регрессия теңдеуінің параметрлерін табыңыз.

2. Корреляцияның дербес коэффициенттерін есептеңіз және корреляцияның жиынтық коэффициентін табыңыз.

3, 5

3, 9

3, 8

5, 7

5, 3

5, 4

3, 2

Х1

Х2

Шешуі:

Екі факторлық регрессия теңдеуін келесі түрде табамыз:

Жиынтық регрессия теңдеуінің коэффициенттерін анықтау үшін нормальдық теңдеулер жүйесі мынадай болады:

№

X₁

X₂

Y²

X₁²

X₂²

Y*X₁

Y*X₂

X₁*X₂

3, 5

12, 25

100

3, 9

15, 21

289

66, 3

31, 2

136

3, 8

14, 44

225

5, 7

32, 49

529

131, 1

39, 9

161

5, 3

28, 09

441

111, 3

21, 2

5, 4

29, 16

484

118, 8

32, 4

132

3, 2

10, 24

144

38, 4

28, 8

108

30, 8

120

141, 88

2212

307

557, 9

193, 5

756

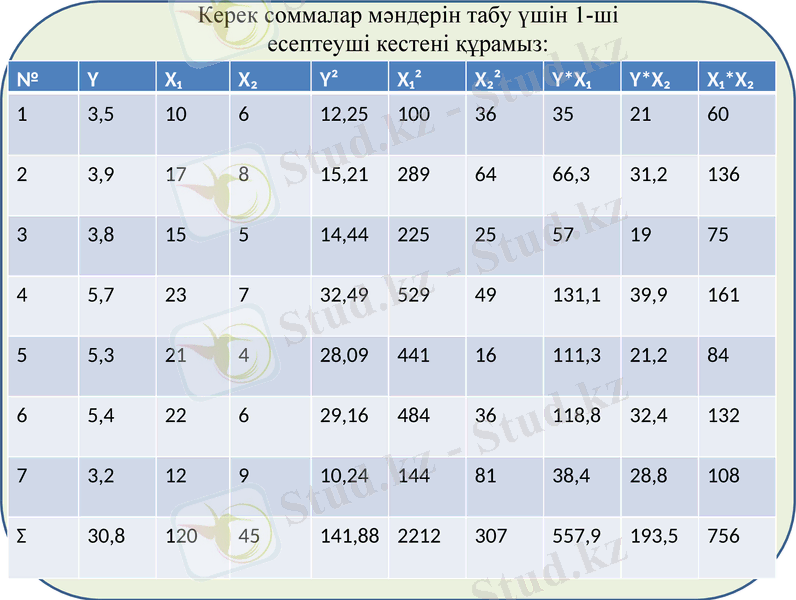
Керек соммалар мәндерін табу үшін 1-ші

есептеуші кестені құрамыз:

Сонда, келесі нормальдық теңдеулер

жүйесін аламыз:

Крамер әдісін қолданып, теңдеулер

жүйесін шығарамыз:

Келесі регрессия теңдеу шығады:

Сонымен, бір жұмысқердің 1 бірлікке өнімнің өндіруі үлкейгенде, пайда 180 мын. тенгеге үлкейеді, экспорттағы өнім үлесі 1 % өскенде, өндіріс концерні 90 мын. тенге пайдалығын жоғалтады.

Экспорттағы бір жұмысқерге өнімнің нөлдік өндіру кезіндегі және өнімнің нөлдік үлесінде, пайда орташа түрінде 1, 86 млн. тенге болады.

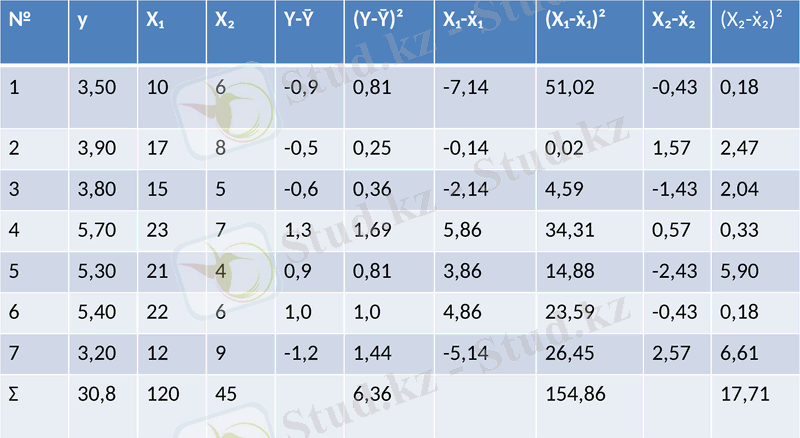
2. Корреляцияның дербес коэффициенттерін және жиынтық корреляция коэффициентін есептеу үшін 2-ші есептеуіш кестені құрамыз, одан бұрын параметрлерінің орта мәндерін және олардың көбейтінділерін есептеп аламыз.