Жұптық сызықтық регрессия және корреляция

Презентация қосу

Жұптық сызықтық регрессия
және корреляция
1. Жұптық сызықтық регрессия.
Оқып білетін белгілер арасындағы мөлшерлі
тәуелділіктердің орнықтылығы әр түрлі
экономикалық зерттеулер үшін маңызды мән
атқарады. Белгілер арасындағы байланыс
корреляциялық( статистикалық ) және
функционалдық ( толық ) болуы мүмкін.
Функционалдық дегеніміз, функцияның бір
айнымалысының әрбір мәніне міндетті түрде
анықталған басқа бір айнымалының мәні сәйкес
келетін белгілер арасындағы байланыс.
Әлеуметтік – экономикалық құбылыстарда
белгілер арасындағы функционалдық байланыс
сирек кездеседі. Мұнда біреуінің әрбір мәніне
екіншісінің бірнеше мәні сәйкес келетін белгілер
арасындағы байланыс кездеседі. Мұндай
байланыс корреляциялық деп аталады.
Корреляциялық байланыс бақылаулардың
үлкен санында айқындалады және сәйкес
математикалық теңдеулермен көрсетіледі.
Түзу сызықты және қисық сызықты, тура және
кері , жай және жиынтық корреляциялық
байланыстарды ажыратады. Корреляциялық
талдау әдісінің көмегімен екі негізгі мәселе
шешіледі:
Байланыс теңдеуінің тұлғасын (формасын) және
параметрлерін анықтау;
Байланыс тығыздығын өлшеу ;
Белгілер арасындағы тәуелділіктер үшін
теңдеулерді таңдап алу корреляциялық талдау
үшін қиыныраққа түседі. Қос корреляция үшін
математикалық байланыс теңдеуі графиктер
көмегімен, корреляциялық кестелерді құрастыру
арқылы, әр түрлі функцияларды жаңадан
қарастыру арқылы орнықтылуы мүмкін.
Экономикалық зерттеулерде көбінесе
ỹx =a+b*x түзу сызық теңдеуімен
анықталатын түзу сызықты тәуелділік
қарастырылады.
Мұндағы ỹx- нәтижелі белгінің түзетілген
мәндері (тәуелді айнымалы),
x- факторлы белгінің мәндері (тәуелсіз
айнымалы),
b-тәуелді айнымалының орташа өзгертілуін
көрсететін регрессия коэффициенті, егер
тәуелсіз айнымалы бірге өзгерсе.
Егер b › 0 болса, онда х-пен у арасындағы
байланыс –тура, егер b ‹ 0 болса, онда байланыс
кері. Бұл теңдеу регрессия теңдеуі немесе
корреляция теңдеуі деп аталады.
2.Ең кіші квадраттар әдісі.
Регрессия теңдеудің а және b параметрлерін
корреляциялық өріс нүктелеріне жақынырақ
өтетін регрессияның теориялық сызығын табуға
болатындай ең кіші квадраттар әдісімен
анықталады, яғни нәтижелі белгінің фактылық
мәнінің түзетілген мәндердің ауытқуының ең
кіші квадраттар қосындысы береді:
Ал a және b параметрлерін анықтау үшін
нормальдық теңдеулер жүйесін шешу
керек:

yi a n b xi
xi yi a xi b xi
Бұл теңдеулер жүйесін Крамер әдісімен
шешуге болады.
Басқаша а және b коэффициенттерін мына
формулалар бойынша табуға болады :
3.КОРРЕЛЯЦИЯ КОЭФФИЦИЕНТI.
КОРРЕЛЯЦИЯЛЫҚ БАЙЛАНЫС ТЕҢДЕУІ РЕГРЕССИЯНЫ Ң ТЕОРИЯЛЫ Қ СЫЗЫҒЫН ЕСЕПТЕУ ҮШІН ҚОЛДАНЫЛАДЫ. БЕЛГІЛЕР АРАСЫНДА ҒЫ ТЫ ҒЫЗДЫҚ БАЙЛАНЫС
Д ӘРЕЖ ЕСІН АНЫҚТАУ ҮШІН КОРРЕЛЯЦИЯ КОЭФФ ИЦИЕНТІ ҚОЛДАНЫЛАДЫ.
ҚОС СЫЗЫҚТЫ Қ КОРРЕЛЯЦИЯ ТӘУЕЛДІЛІГІНДЕ КОРРЕЛЯЦИЯ КОЭФ ФИЦИЕНТІ R МЫНА ФОРМУЛА БОЙЫНША АНЫҚТАЛАДЫ :
;
Қос сызықтық корреляция тәуелділігінде
корреляция коэффициенті r мына форм
формула бойынша анықталады :

x y x y х
r b =
x y у
Мұндағы x x2 (x)2

y y2 (y)2
Корреляция коэффициенттің мәндері
[ -1;1] аралықта өзгереді, яғни
Егер бұл коэффициент онда
белгілер арасындағы байланыс әлсіз ;

Егер онда байланыс орташа;
егер онда байланыс күшті
немесе тығыз.
Егер |r| =1 онда байланыс функционалдық.
Егер r= 0 онда белгілер арасында сызықтық
байланыс жоқ деп айтады. Корреляция
коэффициенті r- дың мәндері әлеуметтік –
экономикалық құбылыстар зерттеуіне үлкен
әсер көрсетеді.
Корреляция коэффициентін есептегенде және регрессия
теңдеуінің коэффициентін тапқанда, кездейсоқ
сипаттамалары бар мәліметтер пайдаланылады.
Сондықтан, сондай мәліметтер негізінде, орнатылған екі
шама арасындағы кездейсоқ байланыс туралы сұрақ туады.
Екі айнымалылар арасындағы байланысты тексеру үшін
корреляциялық түзетуні қолданады:

Мұндағы r- корреляция коэффициенті,
п-таңдама көлемі.
Егер Х пен У арасындағы байланыс маңызды болса,
онда

Регрессия теңдеуінің көмегімен көрсеткіштің
тегістелген мәндерін және ауытқуларын есептеуге
болады. Ауытқулардың қосындысы әрқашан нөлге
тең.
Тегістелген қателік көрсеткіштер ретінде орташа
ауытқуының абсолюттық шамасы болуы мүмкін:
немесе ауытқуының орташа квадраты ( х
бойынша тегістелген у- тін қалдықты
дисперсиясы)

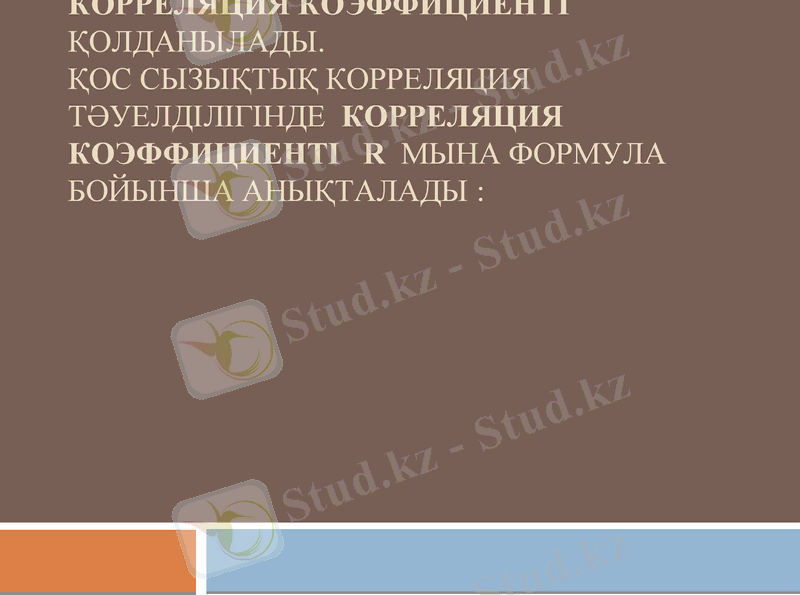
Мысал. Өткен 10 жылдық тауар айналымы
белгілі болсын. Ол кесте арқылы берілсін. Х-
жылдар және У- тауар айналымы (мың тенге)
1. Тауар айналымының уақытқа сызықтық
корреляциялық деп жорып регрессия
сызығының теңдеуін құрыңыз у =а+b*x
2. Корреляцияның сызықтық коэффициентінің
шамасы бойынша x және y белгілер арасындағы
байланыстың тығыздығын бағалаңыз .
3. Тауар айналымының 10 жылының болжамын
анықтаңыз.
4. Регрессия сызығының графигін салыңыз.
Графикте тауар айналымының эмпирикалық
шамаларын көрсетіңіз.
xy x y 1704 16,5 97 103,5
b 2
1,39
x (x) 2 346,5 16,5 74,25

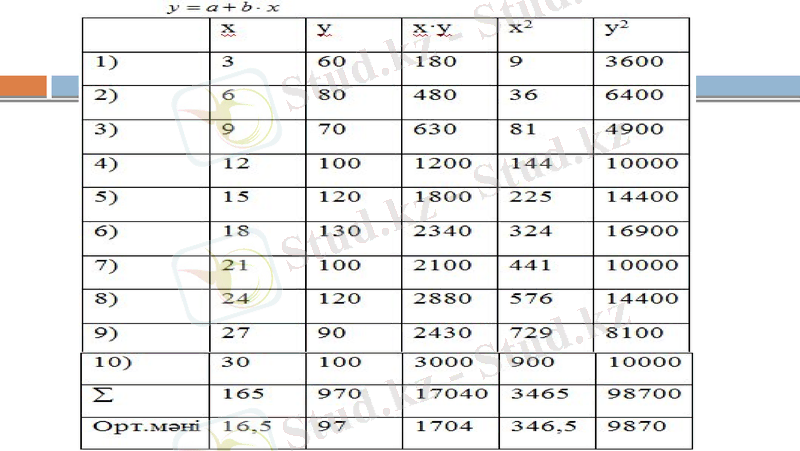
b>0 – байланыс тура

a y b x 97 1,39 16,5 74,07
Y=74,07+1,39X
x x2 (x)2 74,25 8,62

y 9870 97 2 9870 9409 461 21,47

xy x y 103,5 103,5
r 0,56
x y 8,62 21,47 185,07
r = 0,56 – байланыс орташа
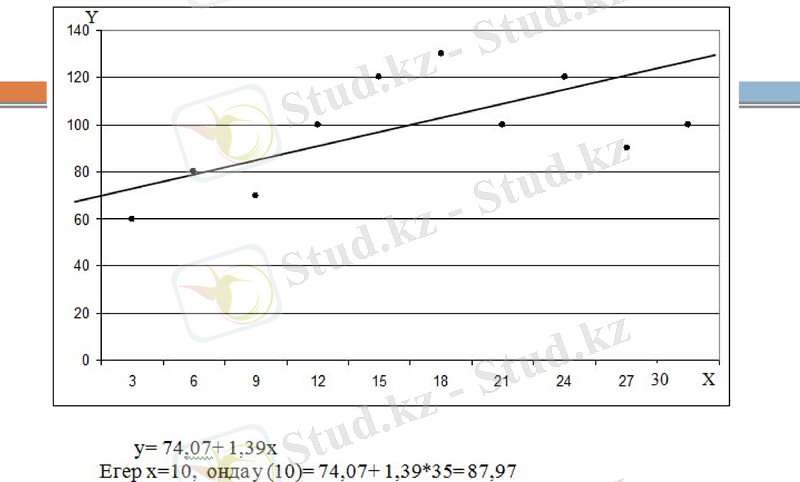
y= 74,07+ 1,39x
Егер x=10,
онда
y (10)= 74,07+ 1,39*35= 87,97

Ұқсас жұмыстар

Регрессия және корреляция параметрлерінің маңыздылық бағасы

СЫНАМА БАҚ ЫЛАУ КАРТАСЫ КОРРЕЛЯЦИЯ

Жиынтық сызықтық регрессия моделі

Автокорреляцияны жою

КӨПТІК СЫЗЫҚТЫҚ РЕГРЕССИЯ МОДЕЛЬ

КОРРЕЛЯЦИЯ КОЭФФИЦИЕНТІН ЭКОНОМИКАЛЫҚ ҚҰБЫЛЫСТАРДЫ ЗЕРТТЕУДЕ ПАЙДАЛАНУ

Регрессиялық талдау

Сапалық зерттеудің негізгі әдістері

Кездейсоқ. жасаушылардың автокорреляциясы

Белгілердің тұқым қуалаушылығы

Пәндер