Регрессия және корреляция параметрлерінің маңыздылық бағасы

Презентация қосу

Регрессия және корреляция
параметрлерінің маңыздылық бағасы.

• 1.Сызықты регрессия және
корелляция параметрлерінің
маңыздылық бағасы.
• Сызықтық регрессияның теңдеуін
тапқаннан кейін оны жалпы теңдеу
ретінде және оның жеке
параметрлерінің маңыздылығына баға
беріледі.
• Регрессия теңдеуінің маңыздылығын
тексеру – айнымалылар арасындағы
тәуелділік математикалық модельге
жататындығын анықтау және
түсіндірілетін айнымалылардың (біреу
немесе бірнеше) жеткілікті енгізілуін
анықтайды.
• Регрессия теңдеуіне мағыналық баға беру
Фишердің Ғ – критерий негізінде жасалады.
Ол регрессия теңдеуінің Н0 болжамының
статистикалық маңыздылығы еместігі мен
байланыс тығыздығының көрсеткішін
тексеруде тұрады. Ол үшін Фишердің Ғ –
критерий мәндерінің факторлық Ғфакт. және
кризистік Ғкриз. (кестелік) мағыналарын
салыстыру қажет. Ғфакт. келесі формула
бойынша анықталады:
2
r xy
Fфакт 2
n 2
1 r xy
r
• Мұнда, xy
-детерминация
коэффициенті;
• п – сандық бірліктердің жиынтығы.
• Ғкриз. – бұл маңыздылық деңгейі мен
еркінділік дәрежелері кезіндегі
максимал мүмкін сан. мағыналық
деңгейі – болжам дұрыс болған кездегі
оның бұрыстығын шығару.
• Көбінесе α 0,05 және 0,01-ге тең деп
алынады.
• Егер Ғ фактолық мәні кестелік мәнінен
үлкен болса, онда Н0 болжамы
қабылданбайды, яғни регрессия
теңдеуінің статистикалық маңыздылығы
мен сенімділігі мойындалады. Қос
сызықтық регрессияда теңдеудің
мағынасы ғана емес, сондай ақ оның
параметрлері де бағаланады. Сондықтан
әрбір параметрі бойынша тв және та
кездейсоқ қателіктері анықталады.
,

• Регрессия коэффициенттерінің
кездейсоқ қателері келесі формулармен
анықталады:
y ~
y x \ n 2
mb
x x 2

~ 2

ma
y yx

x 2

n 2 n x x
• Корелляцияның сызықтық
коэффициентінің маңыздылығы
корелляция коэффициентінің тr қателік
шамасымен анықталады:
1 r 2
mr
n 2
• Регрессия және корреляция
коэффициенттерінің статистикалық
баға берілуі Стьюденттің t критерийі
бойынша анықталады.
• Көрсеткіштердің кездейсоқтық туралы
Н0 болжамы ұсынылады, яғни олардың
нольден айырмашылығы маңызде емес
екені көрсетіледі.
• Регрессия және корелляция
коэффициенттерінің маңыздылық
бағасы кездейсоқ қателік шамасымен
салыстыру арқылы жүреді:

b a r
tb ta tr
mb ma mr
• t - статистикасының фактілік және кризистік
(кестелік) мәндерін салыстырамыз.
• Егер tфакт>tкриз болса, онда Н0 болжамы
қабылданбайды, яғни а, в және rxy
нольден айырмашылығы кездейсоқтық емес
және олар барлығы статистикалық
маңызды.
• Басқаша кезде, көрсеткіштердің кездейсоқ
табиғаты туралы, Н0 болжамы
қабылданады.
• 2. Сызықты емес регрессия
параметрлерінің маңыздылық бағасы.
• Ғ – критерий Фишер бойынша сызықтық
емес регрессия теңдеуінің жалпы
маңыздылығын тексеру
үшінR2детерминация индексі қолданылады.
• дәрежелік функция үшін Ғ –
b
yкритерийін
x a x анықтау сызықтық
байланыстылықта табылатын формуламен
анықталады:
і

R
F 2
n 2
1 R
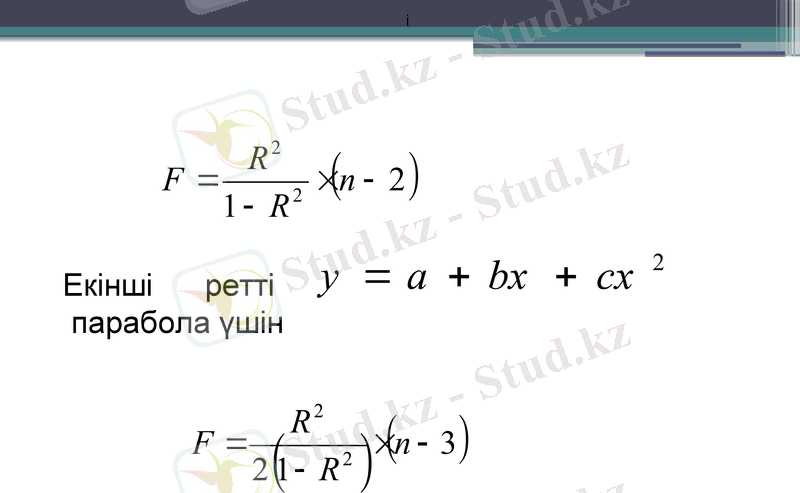
Екінші ретті y a bx cx
парабола үшін

R
F n 3
2 1 R
• 3.Жиынтық регрессия және
корелляция нәтижесінің сенімділік
бағасы.
• Жұптық регрессиядағы сияқты
жиынтық регрессия теңдеуі Ғ –
критерий Фишер арқылы бағаланады:
R2 n m 1
F 2

1 R m
• Мұнда R2-жиынтық детерминация
коэффициенті ( индексі ) ;
• т-модельге қосылған факторлар саны;
• п-бақылаулар саны.
Тек теңдеудің маңыздылығына ғана
баға берілмейді, сол сияқты әрбір
регрессиялық моделіне кірген
факторына да беріледі.
• Өлшем баға болып дербес Ғ-критерийі
қызмет етеді. Екі факторлық теңдеу
үшін дербес Ғ-критерийлер мұнадай
2 2
болады : Fx R yx x r yx
1 2
n 3

1 R yx1 x2

R 2 yx1x2 r 2 yx1
Fx2 2
n 3
1 R yx1x2
.

• Fxi
шамасын біліп, і фактордағы t –
критерийдің регреcсия коэффициенті
tbi

табуға болады,tал атап
F айтқанда,
bi xi
мынаны табамыз
t – критерийі бойынша
Стьюденттің таза регрессия
коэффициентінің мағыналық
бағасын дербес Ғ-критерийлерді
таппай-ақ табуға болады.
• Бұл жағдайда қос сызықтық
регрессияда сияқты, әрбір фактор үшін
мына формула қолданылады:
b i
t bi
b i
mbi
Мунда
-хі факторы кезіндегі регрессия коэффициенті
• mbi b- i регрессия
коэффициентінің
орташа квадраттық қателігі.
y a b1 x1 b2 x2 ... bn xn
• жиынтық регрессияның қателік
коэффициентін анықтау келесі
формуламен жүреді:
y 1 R yx1...xm 1
mbi
xi 1 R 2
xi x1....xm n m 1
• Мұнда y -у белгісі үшін орташа
квадраттық ауытқуы;
• R 2 ух ...х
1 m
- жиынтық регрессия үшін
детерминация коэффициенті;
• - жиынтық регрессия хі
факторының басқа факторлармен
тәуелділік детерминация коэффициенті,
• п-т-1 еркіндік дәрежелерінің
қалдық квадратының сомаларының
ауытқу сандары.
• Дербес корреляция коэффициенті
дербес Ғ-критерийі мен Стьюденттің t
– критерий факторларды іріктеуде
пайдаланылады.

• Біртіндеп шығарып тастау регрессия
теңдеуінде тек қана дербес корреляция
коэффициенттерін сұрыптау арқылы
емес, сондай-ақ tв және Ғх өлшемдері
арқылы да жүреді.
Мысал. Елдің 10 ауданы бойынша
аудандық өнім көлемі (у)
инвестицияларға (х) тәуелділігі зерттелді.
Фишер критериі арқылы сызықтық
регрессиялық модельдеудің
y 13 , 33 7 ,12 x
шешімдерінің статистикалық сенімділігін,
яғни корреляция коэффициентінің
тығыздығы r.
0 , 93 кезінде,
анықтаңыз.
. .

Х 1 2 3 4 5 6 7 8 9 10
У 10 20 40 50 55 70 60 65 80 75

Сызықтық регрессия және корреляцияны Стьюдент критериін қолдану
арқылы маңыздылық деңгейі 0,05 болғандағы параметрлерінің
статистикалық мәнділігін бағалаңыз.

Шешуі.
1) Регрессия теңдеуінің статистикалық маңыздылығын
тексереміз. Ол үшін F – критериінің бақылау мәнін келесі
формула арқылы табамыз:
Fбак ( факт )
r2
п 2
0,93
8 53,23
1 0,93
2 2
1 r

• F – критериінің кестелік мәндері 1 және (n-2)
еркіндік дәрежесі мен мәнділігі 0,05 болғанда F
(0,05; 1; 8) = 5,32 болады, яғни F бақылау F
кризистіктен үлкен болады (53,23>5,32), сонда
мынадай қорытынды істеуге болады: регрессия
теңдеуі статистикалық маңызды және сенімді.
• Регрессия параметрлерінің статистикалық бағалауын
Стьюденттің t – статистикасы арқылы жүргіземіз.
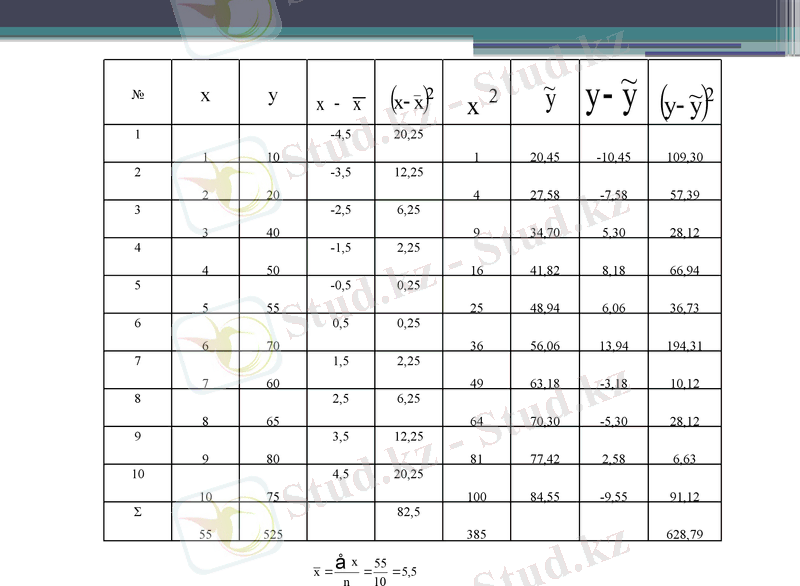
• Есептеуші кесте құрамыз:
№ х у x x 2 2 ~y ~
y y y ~y 2
x x x
1 -4,5 20,25
1 10 1 20,45 -10,45 109,30
2 -3,5 12,25
2 20 4 27,58 -7,58 57,39
3 -2,5 6,25
3 40 9 34,70 5,30 28,12
4 -1,5 2,25
4 50 16 41,82 8,18 66,94
5 -0,5 0,25
5 55 25 48,94 6,06 36,73
6 0,5 0,25
6 70 36 56,06 13,94 194,31
7 1,5 2,25
7 60 49 63,18 -3,18 10,12
8 2,5 6,25
8 65 64 70,30 -5,30 28,12
9 3,5 12,25
9 80 81 77,42 2,58 6,63
10 4,5 20,25
10 75 100 84,55 -9,55 91,12
Σ 82,5
55 525 385 628,79

x
x 55 5,5
n 10
,

• а, в параметрінің және корреляция
коэффициенті r-дың кездейсоқ
қателерін анықтаймыз.
~y 2 2
ma
y

x

628,79 385
6,06
n 2 n x x 2 8 10 82,5

mb
y ~y 2 1
628,79 1
0,98
n 2 x x 2 8 82,5

1 r2 1 0,93 2
mr 0,13
n 2 8
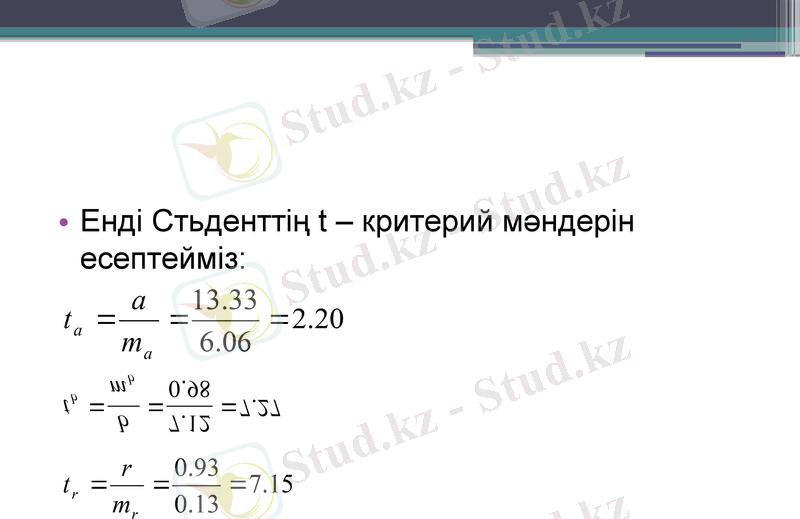
• Енді Стьденттің t – критерий мәндерін
есептейміз:
a 13.33
ta 2.20
ma 6.06
b 7.12
tb 7.27
mb 0.98

r 0.93
tr 7.15
m r 0.13
• 5% маңыздылық деңгейінде және дәреже
еркіндік санында n–2=10–2=8
• t – статистиканың кестелік мәні
• t (0,05; 8)=2,31 болады.
• b және r параметрлерінің t –
статистикалық фактолық мәндері
кестелік мәндерінен үлкен болғаннан,
олардың мәндері статистикалық
маңызды болып саналады, ал параметр
а статистикалық маңызды емес.
• 2. Тұрғын үй нарығын зерттеу үшін
объектінің бағасынан (y-млн. тг.) қала
орталығынан объектінің ара
қашықтығына
x1
• ( -км.)
x 2тәуелділігімен объектінің
пайдалы ауданы ( -км.) бойынша
y 1құрылған:
мына теңдеуі ,86 0,18x1 0,09x 2
,
,
.

• Сонымен бірге жиынтық корреляция
коэффициентіR yx1x 2 0,96 алынған
және қосақты корреляция
коэффициенттері
ryx1 0,95 ryx2 0,42 rx1x 2 0,29
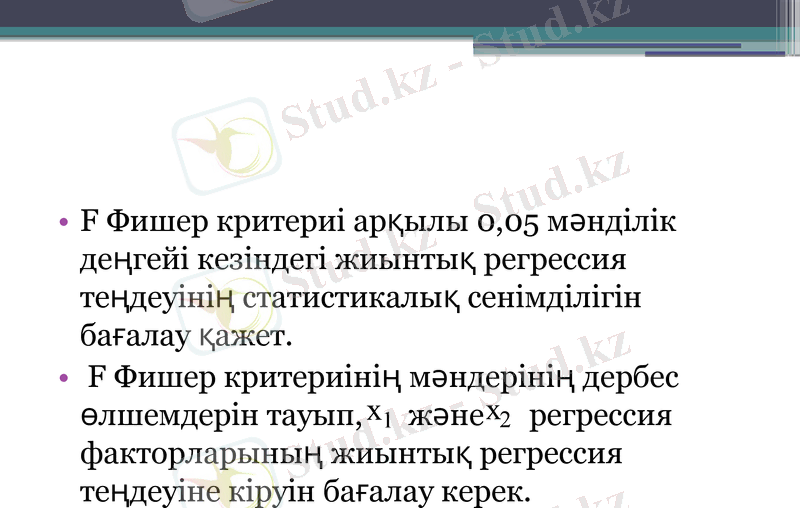
• F Фишер критериі арқылы 0,05 мәнділік
деңгейі кезіндегі жиынтық регрессия
теңдеуінің статистикалық сенімділігін
бағалау қажет.
• F Фишер критериінің мәндерінің
дербес өлшемдерін x2
x1 тауып, және
регрессия факторларының жиынтық
регрессия теңдеуіне кіруін бағалау
керек.
•x1 жәнеx2 айнымалылары кезінде
• t – Стьюдент критериін қолданып
коэффициенттердің статистикалық
маңыздылығын бағалаңыз.
• Шешуі. Регрессия теңдеуінің
маңыздылығын жалпы F Фишер
критериі арқылы 2 бағалаймыз.
R yx x n m 1 0,96 2 4
Fфакт 2

23,51
1 R yx x m 1 0,96 2
1 2
• m және (n-m-1) еркіндік дәрежелері
кезінде F Фишер критериінің кестелік
мәні мен 0,05 мәнділігі Ғ (0,05; 2;
4)=6,94 болады,
• яғни Ғ фактолық мәні кестелік мәнінен
асып тұр, сондықтан теңдеудің жалпы
статистикалық мәні жөнінде шешімдер
жасауға болады (23,51>6,94)
• Fx дербес критериілер бір факторды
басқа фактордан кейін енгізу
мақсаттығын бағалайды.
• Fx1 дербес критериі х1-ді х2-ден кейін
енгізудің дұрыстығын бағалайды.
R 2yx1x 2 ryx
n m 1 0,96 2
0, 42 2
Fx1 2
38,02
1 R yx1x 2 1 1 0,96 1
.

• 1 және (n-m-1) еркіндік дәрежелері
кезінде F-критериінің кестелік мәндері
және 0,05 F 0 , 05 ; 1 ; 4 7 , 71
x1 деңгейі
• мәнділік x2
• болса, -ді - ден кейін енгізуді
жөн көреміз,
F x1 өйткені
F криз
(38,02>7,71)
Fx 2 x2 x1
дербес критериі - ні - ден
кейін енгізуді көрсетеді:
R 2yx1x 2 ryx
n m 1 0,96 2 0,95 2 4
Fx 2 2
0,97
1 R yx1x 2 1 1 0,96 1

• 1 және (n-m-1) еркіндік дәрежелері
кезінде F-критериінің кестелік мағынасы
және 0,05 мәнділік деңгейі
F 0 , 05 ; 1 ; 4 7 , 71
• болады, факторлық және кестелік
мәндерін салыстырғаннан кейін мынадай
шешімгеxкелеміз:x -ді - ден
1 2
кейін енгізуді маңызды емес,F F өйткені x2 криз
,

b1 және b2 коэффициенттер
маңыздылығын - Стьюдент критериі
арқылы бағалаймыз. F- Фишер
критериінің дербес мәнінен - критерийді
түбір
t b ретінде
Fx 38,02табамыз:
6,16 t b F x 0 , 97 0 , 99
2 2
1 1

• (n-m-1) еркіндік дәрежелі кезінде және
0,05 мәнділік деңгейі t (0,05;4)=2,78
болады. Алынған мәндерді салыстырып,
мына қорытындыға келеміз:
(

• b1 коэффициенті статистикалық
маңызды жәнеt сенімді
b1 tкриз ( ),
• ал b2 коэффициенті керісінше, маңызды
t t
да сенімді де емес
b2
(криз
).

Ұқсас жұмыстар

Жиынтық сызықтық регрессия моделі

Регрессиялық талдау

Автокорреляцияны жою

Жұптық сызықтық регрессия және корреляция

СЫНАМА БАҚ ЫЛАУ КАРТАСЫ КОРРЕЛЯЦИЯ

Гетероскедастикалық. Гетероскедастикалықты анықтау тесттері

Белгілердің тұқым қуалаушылығы

КОРРЕЛЯЦИЯ КОЭФФИЦИЕНТІН ЭКОНОМИКАЛЫҚ ҚҰБЫЛЫСТАРДЫ ЗЕРТТЕУДЕ ПАЙДАЛАНУ

Урбандалу процестерін моделдеудің ақпараттық жүйесін құру

Кездейсоқ. жасаушылардың автокорреляциясы

Пәндер