1-модуль. Галактика модельдерін түзу. Галактиканың спиралдық құрылымы

Презентация қосу

Қолданылатын әдебиеттер
Негізгі:
1. Гинзбург В.Л. Теоретическая физика и
астрофизика. М.: Наука. 1981
2. Хоперсков С. А. Эволюция дисковых галактик:
исследование иерархии структур. Дисс. на соиск.
учен. степ. канд. физ.-мат.наук : 01.03.02/
Моск.гос.ун-т им.М.В.Ломоносова.- М., 2013.
3. Фридман А. М. Предсказание и открытие новых
структур. УФН, т.177, №2. 2007

Қосымша:
4. Мартынов Д.Я. Курс общей астрофизики. 2 изд., М.,
1971.
1-модуль. Галактика
модельдерін түзу.
Галактиканың
спиралдық құрылымы.
Жұлдыздар жүйе динамикасы деп жұлдыздар жүйесінің қасиеттер мен
тартылыс күштердің әсерімен осы жүйелердің эволюциясын зерттейтін
астрономияның бір бөлігі. Жүйенің эволюциясы массаның таралуы мен
массалардың қозғалысын анықтайды.
Иррегулярлық күштер деп жұлдыздардың өзара әрекеттесу күштері.
Регулярлық күштер деп жұлдызға уақытша әсер ететін жүйе
объектілерінің әсері.
Балдж деп спиралды галактикалар құрылымының элементі. Яғни, өлшемі
бірнеше жүздеген парсектен килопарсекке дейін жететін галактиканың
сферасындағы ішкі жарық бөлігі болып табылады. Ол галактикада созылған
орбита бойынша қозғалатын кәрі жұлдыздардан тұрады.
Галактиканың бары дегеніміз спиралды және дұрыс емес галактика
құрылымдарының элементтері. Ол диск жазықтығында жатқан созылыңқы
тығыз жұлдыздар мен жұлдызаралық газ тәрізді. Бардың центрі диск
центрімен сәйкес келеді. Егер галактикада бар болса, онда спиралдық
Жұлдыздар жүйесінің динамикалық қасиеттері
Жұлдыздар қозғалысының жалпы қасиеттерін мынандай
әдістер арқылы анықтауға болады:
Жұлдыздар жұлдыздық газды құрайтын материалдық нүкте
сияқты қарастырылады.
Жұлдыздар жылдамдығының дисперсиясы газдың
қарапайым температурасының өлшемінің рөлін атқарады.
Тартылыс күші арақашықтықпен жаймендеп азайып
отырады. Сондықтан да потенциалдық энергия есебінде
жұлдыздар жүйе көлемінде жұлдыздардың ішкі
гравитациялық әрекеттесуді ғана емес, жүйенің басқа да
бөліктерінің әрекеттесуін ескеру қажет.
Жұлдыздар Галактика жазықтығында аз
орналасқандықтан, араларындағы тығыз жақындасу да аз
болады. Сондықтан Галактикадағы жұлдыздардың еркін
жүгіруі Галактика өлшемінен әлдеқайда үлкен болады.
Жұлдыздар араларындағы әрекеттесу өлшемі
иррегулярлық күш болып табылады.
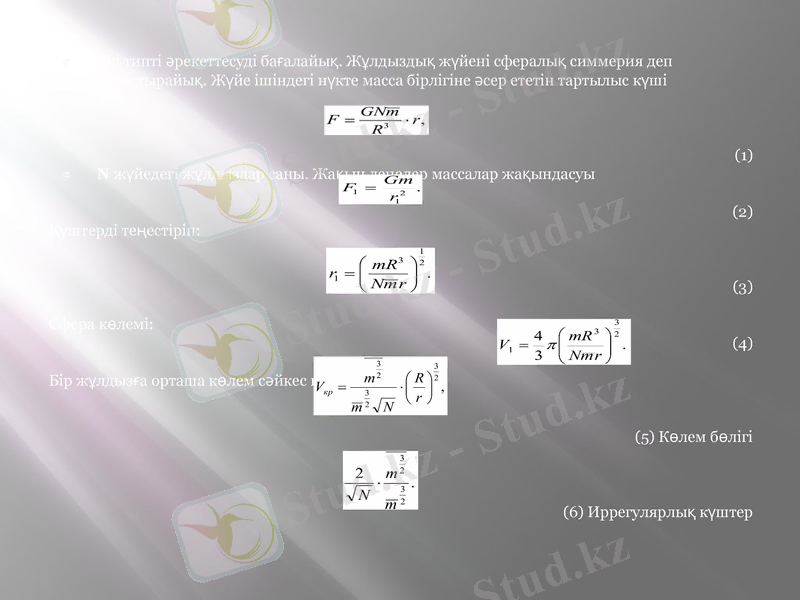
Екі типті әрекеттесуді бағалайық. Жұлдыздық жүйені сфералық симмерия
деп қарастырайық. Жүйе ішіндегі нүкте масса бірлігіне әсер ететін тартылыс
күші

(1)
N жүйедегі жұлдыздар саны. Жақын денелер массалар жақындасуы

(2)
Күштерді теңестіріп:

(3)

Сфера көлемі:
(4)

Бір жұлдызға орташа көлем сәйкес келеді:

(5) Көлем бөлігі

(6) Иррегулярлық күштер
Галактикада жұлдыздар аса айырымы жоқ массалардан тұрады.
Галактикадағы N жұлдыздар саны өте көп. Екінші бөлшегі бірге
жақын. Сондықтан көлемнің бөлігі аз болады. Галактикадағы
жұлдыздар дискісінде парадокс бақыланады: бір жағынан,
жұлдыздар дискісінде жылдамдықтардың элиссиалдық
таралулары бақыланса, олар релаксациялық процестер, екінші
жағынан жұлдыздық газдың бөлшектерінің еркін жүріс уақыты
Галактика уақытытынан көп болып келеді. Бұл дегеніміз жұлдыз
жұлдыздық жақындасу эффективті емес.
Бұл қатынас өзгеру мүмкін еді, егер де гигант молекулалық
бұлттар Галактика массасының үлкен бөлігін құраған болса. Бірақ
та олай емес, жұлдызаралық ортаның массасы 5-10% құрайды.
Жұқа дисктегі жұлдыздар релаксациясына әкелетін объектілердің
негізгілері болып гравитациялық потенциалдың қозуы болып
табылады. Спиралды бұтақтардың аз екеніне қарамастан,
олардың жоғарғы массасы мен әрекеттесуі жеткілікті екен.
Статикалық физикаға сәйкес, материалдық нүктелердің
жүйесін фазалық тығыздық функциямен сипаттауға болады.
Жұлдыздық жүйе стационар деп атайды, егер де оның функциясы
уақытқа байланысты болмаса. Жұлдыздар жүйесін стационарлық
емес деп жиі айтады, егер де күй өзгерісі жай болса.
ЖҰЛДЫЗДАР ЖҮЙЕ ҚОЗҒАЛЫСЫНЫҢ
СИММЕТРИЯСЫ МЕН ИНТЕГРАЛДАРЫ
Жұлдыздар жүйесінің фазалық функциясының қасиеттерін қарастырайық.
Жұлдыздар нүктелік тартылатын массалар тәрізді қарастырылады. Фазалық
тығыздықтың функциясы алтыөлшемді фазалық жазықтықтағы жұлдыздар
элементінің ықтималдылықтар таралу тығыздығы сияқты анықталады. (7)
(7)

Фазалық тығыздық функциясының интегралдануы жылдамдық
бойынша жүйедегі жұлдыздар жазықтықта таралады. Ал
интегралдану жүйедегі нүктелердің жылдамдығы бойынша
таралады. Физикалық мағынасы бойынша фазалық тығыздық
функциясы барлық жерде оң шама болады.
(8)
Ф(x,y,z,t) – жүйенің гравитацциялық потенциалы.
Фазалық кеңістікте қозғалатын жұлдыздар тобын қарастырайық. t
және t+dt, яғни. Ψ(t) = Ψ(t + dt) моментте жұлдыздар саны
өзгермеді. Сызықтық біртекті дифференциалдық теңдеу:
(9)

Бұл теңдеу жұлдыздық динамиканың фундаменталдық теңдеуі болып
табылады.
Теңдеудің шешімі
(10)

Егер біз теңдеуді гравитациялық потенциал үшін жазсақ, жүйеде
алты интегралды таба аламыз.
Егер жұлдыздар жүйесі симметриялы болса тапсырма
оңайланады. ХХ ғасырда дәлелденген Нетер теоремасына сәйкес:
әр үздіксіз бір параметрге негізделген, функционал әрекеті
өзгермейтін формулада қозғалыс теңдеуінің интегралы, сақталу
заңы сақталады. Мұндай түрлендірулерге симметрия
түрлендірулері жатады. 1915 ж Джинс теореманы көрсетті: жақсы
араласқан жұлдыздар жүйесіне фазалық тығыздық функциясы
қозғалыс интегралының функциясы ретінде жазылуы мүмкін: Ψ =
Ψ(I1,...,I6). Ψ қозғалыс интегралының нақты түрін беру керекпіз.
Өйткені бізді Ψ функцияның кеңістіктегі координатағы тәуелділігі
қызықтырады. Фазалық тығыздық функциясының нақты түрін
жұлдыздар жүйесінің бақылауларынан ғана таба аламыз.
Бірнеше мысалдар қарастырайық:
1) Фазалық тығыздық функциясы мен потенциалы уақытқа байланысты
болмасын: . ∂Ψ/∂t жүйе стационарлы болсын.

(11)

Осы теңдеуді қоссақ:
(12)

Оң жағы да сол жағы да дифференциал болып табылады.
Сондықтан да интегралдап: V2 = 2Ф + const. (13) Теңдеуді аламыз.
Потенциалды сол жаққа ауыстырсақ, энергия интегралы үшін
теңдеді аламыз: : I1 = V2 - 2Ф. (1о) теңдеуде интеграл болмаса,
фазалық тығыздық функциясы Ψ = Ψ(V2 - 2Ф), жылдамдықтар
таралуы сфералық симметрия болатын еді. Бұл жағдай
Галактикада болмайды.
Егер жұлдыздың жылдамдығы V2 - 2Ф > 0 болса, онда то V >
(2Ф)1/2 еді және жұлдыз жүйеден кететін еді. V = (2Ф)1/2 шарты
жұлдыздар жүйесінде критикалық жылдамдықты анықтайды.
2) Егер потенциал сфералық симметриялы болса, онда I1 басқа үш аудан
интегралын аламыз. (14)

Фазалық тығыздық функция үшін шешімі: Ψ = Ψ(I1,I2,I3,I4). Сфералық
симметриялы болуы үшін, фазалық тығыздық функциясы
координатаға емес, радиус векторге байланысты болады: r = (x 2 +
y2 + z2)1/2 . Бұл шартты бұрыштық моменттке ауыстырамыз:
сфералық координата.

(15)

Мұндағы I22 + I32 + I42 = r2(VΘ2 + Vφ2). Бұл жерде фазалық тығыздық
функциясы бар. Мұнда біз бұрыштық айнымалыдан тұратын бірдей
осьті жылдамдық эллипсиодын көре аламыз.
3) Цилиндрлік симметрия жағдайын қарастырайық. Энергия
интегралынан басқа бір аудан интегралын таба аламыз: I2 = xv - yu =
const

Цилиндрлік галактоцентрлік координаталар жүйесінде I2= RVΘ.
Теңдеудің жаңа шешімі болып:

Жылдамдық компоненттері фазалық тығыздыққа симметриялы
болады. Жылдамдық эллисиодтары екі бірдей осьті болады.
Жоғарыда айтылған жағдайларда интегралдардың толық түрін
ала алмаймыз. Галактиканың симметриялы интегралдары үшін ось
бойынша қозғалатын Галактика жазықтығында жатқан
интегралдарды алдық.
Стационарлық Галактика
(9) негізгі теңдеуді екі жағдайда қолдануға болады. Фазалық тығыздық
функциясы үшін шешім табу немесе Галактика потенциалын тауып, Пуассон
теңдеуі арқылы массалар таралуын табу болып табылады.
ХХ ғ. 20-жылдары Оорт зерттеу жүргізді: Галактиканың стационарлық пен
цилиндрлік симметриялығынан басқа, фазалық тығыздық функциясына жақын
Шварцшильд таралуы.
(16)

где vΘo – центроидтің айналу жылдамдығы. Жылдамдықтың кері дисперсиясы үшін:
(17)

Жылдамдықтар дисперсиясы Галактика радиусы мен перпендикулырлы
жазықтықтта бірдей болады. Ал жылдамдықтар дисперсиясы галактика айналу
бағытында Галактика арақашықтығы мен айналу осіне байланысты болады.
Айналмалы жылдамдық үшін:

(18)
Галактикалық жазықтықтағы гравитациялық потенциал формасы:

Потенциал нолге тең болу керек. R = 0 болған кезде Ф = Ф с. (19) Паренаго
потенциалын Галактикаға таратуға болады. Мысалы, |z| немесе exp(-z2) көбейту
арқылы.
ХХ ғ екінші жартысында Галактиканың гравитациялық потенциалы үшін
көптеген теңдеулер ұсынылды. Соның біреуі Линден Белл потенциалы.

Мұндағы G – тартылыс тұрақтысы, M – Галактика массасы. Қисық айналуда:
Стационарлық шарт пен жылдамдықтың шварцшильд
таралуы бақыланатын мәліметтерге кері болып келеді.
Жылдамдықтар эллипсиоды үш осьті болады, ал қисық
айналу жай модельдерге қарағанда өте күрделі болады.
Негізгі теңдеудің сызықтылығы, яғни фазалық тығыздық
функциясы мен Пуассон теңдеуінің сызықтылығы, яғни
заттың потенциалы мен тығыздығы Галактиканың әр
түрлі жүйелерінің қосындысы түріндегі потенциалды
табуға болады.
Галактиканың құрамдық
модельдері
Галактика күрделі құрылымды болады және әр түрлі кеңістіктік кинематикалық
қасиетті жүйелерден тұрады. Галактиканың құрылымы жайлы бірнеше сұрақтар
туындайды: Галактикада қанша жүйелерді алу керек, олардың геометриялық
сипаттамалары қандай, осы жүйелерден тұратын Галактиканың массасы қалай.
Келесі қадам болып жүйелердегі массалардың таралуы және жұлдыздар
жылдамдығының дисперсисиясы, жылдамдық дисперсиясы мен галактика
координаталарының қатынасы.
Осы сұрақтарға Галактиканың модельдерін түзу арқылы жауап алуға болады:
жүйелерге бірнеше сипаттамалар қойып, олар бақыланатын мәліметтермен қалай
байланысты деген жауаптар. Бақыланатын мәлімет ретінде Галактиканың қисық
айналуы, жүйелердегі жылдамдық диперсиясы, Күннен тыс зат тығыздығының
өлшемі қолданылады. Нақты бақыланатын мәлімет ретінде Галактиканың көп
компонентті модельдерін аламыз: балдж, диск, гало тәрізді компоненттер. Ең әйгілі
модель Шмидт моделі болып келеді. Ол модель ХХ ғ 60 ж пайда болды. Ол бірнеше
сығылған сфероидтан тұрады. Модельдің пайда болуы: тартылыс күші
(22)

Мұндағы е - сфероид сығылуы, α – үлкен жарты осьтің арақашықтығы.
Қазіргі таңда жүйені ядро, балдж, гало, диск, тәж деп есептеуге болады. Тәж
жасырын массаны қамтамасыз етеді.
Галодағы заттың тығыздығының таралуын сфералық симметриялы деп
есептейді және дәрежелі қатынас түрінде беріледі. Сондай ақ дәрежелі қатынас
ретінде балдж тығыздығын да алуға болады. Ал гало үшін Вокулер заңын:
галактика жарықталу қолдануға болады. Галодағы массалардың тығыздығына
дәрежелік қатынасты қоюға болады. Дисктегі массалардың таралуын
арақашықтық пен айналу осінің қатынасының экспоненциалдық түрде беруге
болады. Бұл теңдеуді: (22)

Sch гиперболалық секанс.
Галактика жазықтығының үстіндегі потенциалға жауап беретін параметрлер
жұлдыздардың санағынан алынған z-бағыттағы зат тығыздығы ретінде
бағаланады.
Зерттеушілердің тобы кп құрамдас модельдер ойлап табылды. Модельдер
параметрлері кестеде көрсетілген.
Подсистема α0, кпк M (1010 M¤ ) ε
Кесте 1. Галактика модельдерінің параметрлері
Ядро 0.005 0.009 0.6
Балдж 0.2 0.45 0.6
Гало 2 1.2 0.3
Диск I 4.6 7.7 0.1
Диск II 1.0 -0.4 0.45
Плоская I 6.4 1.0 0.02
Плоская II 5.1 -0.6 0.025
Корона 75 110 1
α0 Галактика жазықтығының сфероид өлшемі. М – күн массасындағы масса. ε
= b0/α0 – сфероидтың қосындысы.
Жүйенің параметрлері бақыланатын қисық айналу болатындай және
галактика тұрақты жүйесінен тұратын алу жолында орналасады. Ядро үшін
параметрлер Андромеда тұмандығының ядросынан алынған. Балдж радиусы
мен массасы қисық айналудың бірінші максимумдар анықталған. Галоның
радиусы шар тәрізді шоғыр кеңістіктік таралуы негізінде анықталған. Ал
масса тығыздық пен жұлдыздардың тығыздық градиенті негізінде
сипатталады. Диск параметрлерін анықтауда бұл модельде минимум
облыстағы қисық айналу формасын қалыптастыруға болмайды. Егер де
Галактика центрінен тығыздықтың экспоненциалдық азаюын қолдансақ.
Сондықтан да кестеде көрсетілген теріс масса компоненттерін алуымыз
керек. Тәждің массасы мынандай жағдайда: жақын ергежейлі галактикалар,
жұлдыздар жүйесінің серіктері Галактиканың гравитациялық өрісімен
ұсталып қалады. Галактиканың толық массасының бағасы (1.8 - 2.5)•10 12•М¤
мәнге әкеледі. Бұл мәнді жапондық астрономдар Сакамато, Чиба, Бирс
тапты. Осы ергежейлі галактикалардың жылдамдығының дисперсиясының
өлшемі бойынша тәж массасы вириал теорема арқылы есептеледі. Ал оның
өлшемдері осы галактикалардың жүйесінің өлшемі ретінде бағаланады.
Тәждің үлкен массасы Галактиканың тез қозғалатын серіктерін ұстау үшін
және қисық айналуды түсіндіру керек дейміз. Мұндай масса Галактика
дискісінің стабилизацисы үшін және тез бұзылуы үшін керек. N дененің
тапсырмасының шешімі бойынша сандық эксперименттер жұлдыздық дискте
спиралды галактикаларды еске түсіретін тығыздықтың тез өсуі тез көрінеді.
Соңында барлық диск барда жиналады. Бірақ тұрақсыздық көрінеді.
Ең маңызды сұрақ болып: тәждің қара заты неден тұрады?
Бұл сұрақ осы уақытқа дейін шешілмеді. Хаббл атындағы
ғарыштық телескоппен бақыланған бақылаулар жетпейтін
массаны кәрі ақ ергежейлілер құрайды деп көрсетеді. Тәж
массасы аккрециялық объектілер шар тәрізді шоғырлар мен
жұлдыздар құрайды. Қазіргі таңда Галактика тәжін құрайтын
объекттерді іздеуге микролинзаланған бақылау
бағдарламалары шығарылды. MACHO (Massive Compact Halo
Objects галоның массалық компакттық объектілері) және OGLE
(Optical Gravitational Lensing Experiment) бағдарламалары. MACHO
бағдарламасында Үлкен Магеллан бұлттары бағытындағы 12
миллион жұлдыздардың зерттелуі мен Галактиканың балджы
жүргізілді. Линзалынған объектілердің көбісі 0.15 пен 0.9 күн
массасында орналасады. Тәжде мұгдай объектілер 2• 1011 болу
керек, тәждің қара материясы суық ақ ергежейлілерден
тұрады. Қазір 250 км/с жылдамдықты 46 ақ ергежейлі белгілі.
Жұлдыздық статистиканың интегралдық
теңдеулері
Галактика модельдерін тексеру үшін жұлдыздық санақтар
қолданылады. Соңғы онжылдықта жұлдыздық санақтар қуатты
телескоптардың пайда болуымен байланысты. Галактика модельдерін
тесеру үшін жұлдыздық санақтарда жұлдыздық статистиканың
интегралдық теңдеулері қолданылады.
(24)
где М – абсолюттік жұлдыздық шама, D(r) – жұлдыз тығыздығы, φ(М)
жарықтылық өлшемі. (24) интегралдап:
(25)

теңдеу Шварцшильд бірінші теңдеу деп аталады, ол жұлдыз тығыздығы
мен жарқырау функциясын байланыстырады. Егер жұлдызға дейін
арақашықтық немесе π = 1/rтағы да параллакс таралуы белгілі болса бір
теңдеу алуға болады. Әр жұлдыздың параллакс көбейтсек: (26)
ХХ ғ бірінші жартысында жұлдыз тығыздығын
анықтайтын теңдеулер ойлап табылды. Бірақ мұндай
зерттеулердің шешімдері қанағаттандырлынбаған
болды. Мұндайда екі себеп бар. Біріншісі, қазірде
Галактика жұтылатын материялардың таралулары аз.
Ал екіншіден, осы теңдеулердің шешімі тұрақсыз
болды.
Қазіргі таңда интегралдық теңдеулер кері
тапсырманы орындау үшін Галактика модельдерінен
жұлдыздар тығыздығы бойынша тапсырмалар
қолданылады. Салыстыру үшін жарық ұтылуы аз
облыстар таңдалады. Мысал .1 суретте көрсетілген.
Мұнда жұлдыздар санағының шешімдері Бакал және
Сонейр Галактика модельдерінде негізделген
жылтырау функциясымен салыстырылады. Сурет
модельдеу шешімдері мен бақыланған мәліметтердің
дұрыстығын көрсетеді: V ≈ 20m.
Сурет 1.

Ұқсас жұмыстар

ӘЛЕМ ҚҰРЫЛЫСЫ МЕН ЭВОЛЮЦИЯСЫ

Бірінші жұлдыздардың пайда болуы

Әлемнің ірі масштабты құрылымын бейсызықты талдау

Жас табиғаттанушылар сайысы

Галактикалар жүйесі

Cyclone 6.0 программалық қамтамасыздандыру

Қүн жүйесінің алғашқы ұғымдары

Интеллектуалды ақпараттық жүйелер

ANSYS CFX программа пакеті

Ғарыштың зерттеулерғарышта заттық құрамы

Пәндер