ГАЛАКТИКА ФОРМАСЫН СИПАТТАЙТЫН ҮШ ӨЛШЕМДІ БЕЙНЕЛЕУ

ГАЛАКТИКА ФОРМАСЫН СИПАТТАЙТЫН

ҮШ ӨЛШЕМДІ БЕЙНЕЛЕУ

Зерттеудің актуалдығы

Галактикалар пайда болуы мен эволюциясы барысында көптеген морфологиялық өзгерістерге ұшырайды. Бұл құрылымдылық ерекшеліктерді зерттеу арқылы галактикаларда болып жатқан сан алуан процесстер мен механизмдерді түсіну мен заңдылықтарды ашу актуалды мәселе.

Бүгінгі күні, кұңгірт энергия және қараңғы материя түсініктерімен байланысты сұрақтарға жауап іздеу - космосты зерттеуде ерекше рөл ойнайды. Ал бұл эффекттер алыс галактикалар құрылымы мен әсерлесу динамикасынан бақыланады.

Мәселенің қазіргі күйі

Галактикалардың құрылымдық ерекшеліктеріне жауапты процесстер мен механизмдерді эксперимент жүзінде, немесе нақты уақыт аралығында динамикасын тікелей зерттеу мүмкіндігінің принципиалды түрде болмауы - бұл бағытта компьютерлік модельдеу ролін арттырады. Бұл модельдерде баршалықты мүмкін физикалық заңдылықтар мен факторлары ескеріп, бақылау нәтижелерімен салыстыру - теориялық зерттеулер негізін құрайды.

Жұмыстың мақсаты

Үш өлшемді бейнелеу арқылы галактикалар формасын модельдеп, информациялық - энтропиялық талдау жасау.

Зерттеу әдістемесі

Жанабаев З. Ж. Квазиканоническое распределение Гиббса и масштабная инвариантность хаотических систем // Мат. 5-й межд. конф. «Хаос и структ. в нелин. сист. », 15-17 июня, 2006. Астана. - Ч. 1. - С. 15-23.

(1)

(2)

(3)

(4)

S - Шэннон энтропиясы, P(i) - ықтималдылық

- Толық энтропия, - Шартты энтропия,

- біртектілік дәрежесі

- Мультифракталдық өлшемділік, - Реньи энтропиясы,

- Хаусдорф өлшемділігі.

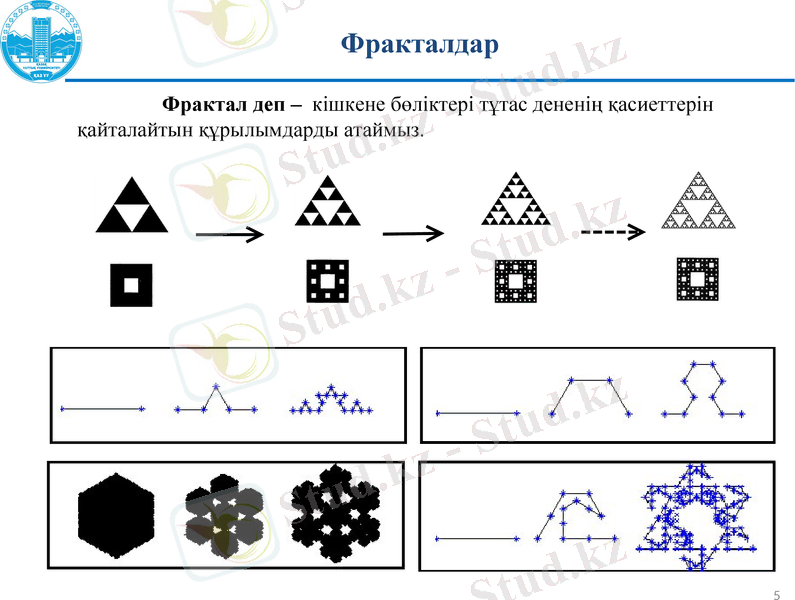
Фракталдар

Фрактал деп - кішкене бөліктері тұтас дененің қасиеттерін қайталайтын құрылымдарды атаймыз.

Зерттеу нәтижелері

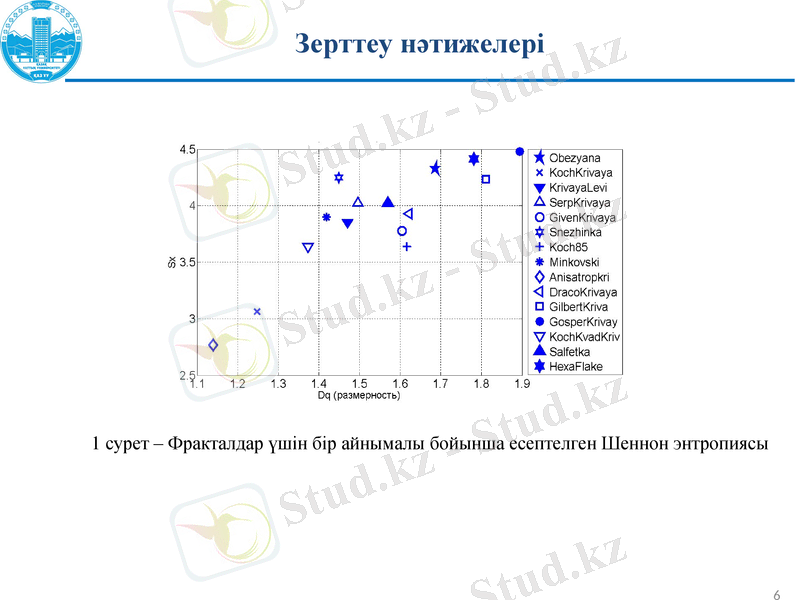
1 сурет - Фракталдар үшін бір айнымалы бойынша есептелген Шеннон энтропиясы

Информациялық - энтропиялық диаграмма

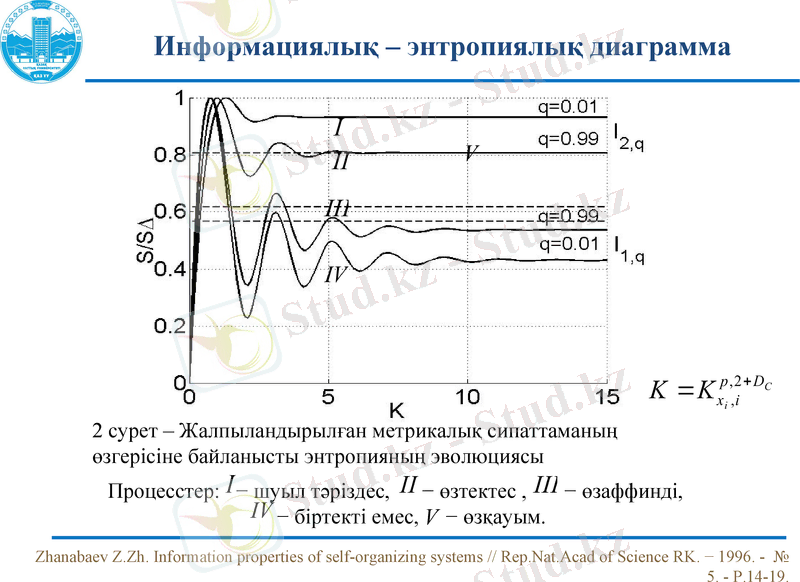
Процесстер: − шуыл тәріздес, − өзтектес, − өзаффинді,

− біртекті емес, − өзқауым.

2 сурет - Жалпыландырылған метрикалық сипаттаманың өзгерісіне байланысты энтропияның эволюциясы

Zhanabaev Z. Zh. Information properties of self-organizing systems // Rep. Nat. Acad of Science RK. − 1996. - № 5. - P. 14-19.

Зерттеу нәтижелері

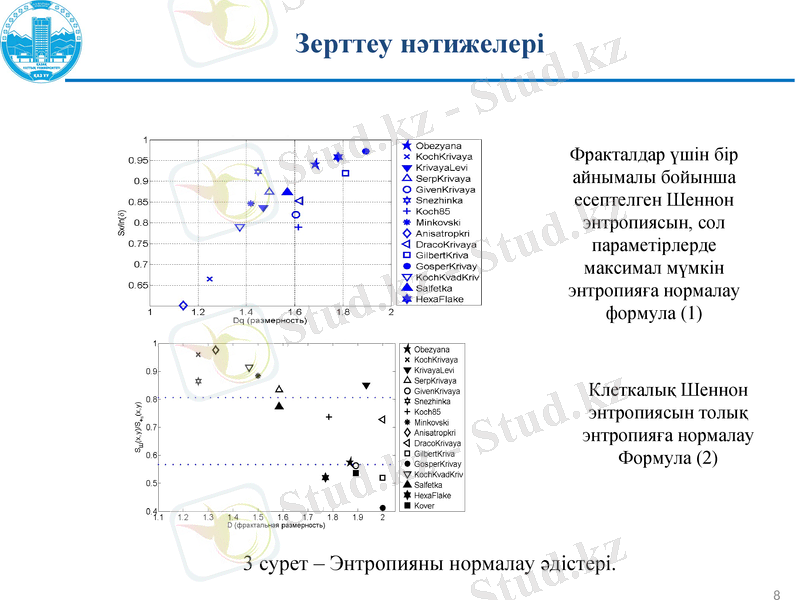
Фракталдар үшін бір айнымалы бойынша есептелген Шеннон энтропиясын, сол параметірлерде максимал мүмкін энтропияға нормалау формула (1)

Клеткалық Шеннон энтропиясын толық энтропияға нормалау

Формула (2)

3 сурет - Энтропияны нормалау әдістері.

Зерттеу нәтижелері

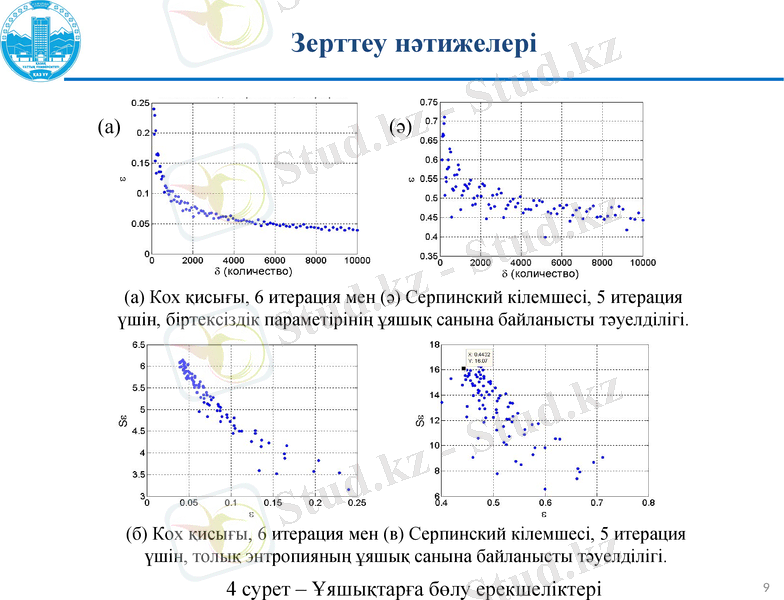
(а) Кох қисығы, 6 итерация мен (ә) Серпинский кілемшесі, 5 итерация

үшін, біртексіздік параметірінің ұяшық санына байланысты тәуелділігі.

(б) Кох қисығы, 6 итерация мен (в) Серпинский кілемшесі, 5 итерация

үшін, толық энтропияның ұяшық санына байланысты тәуелділігі.

(а)

(ә)

4 сурет - Ұяшықтарға бөлу ерекшеліктері

Зерттеу нәтижелері

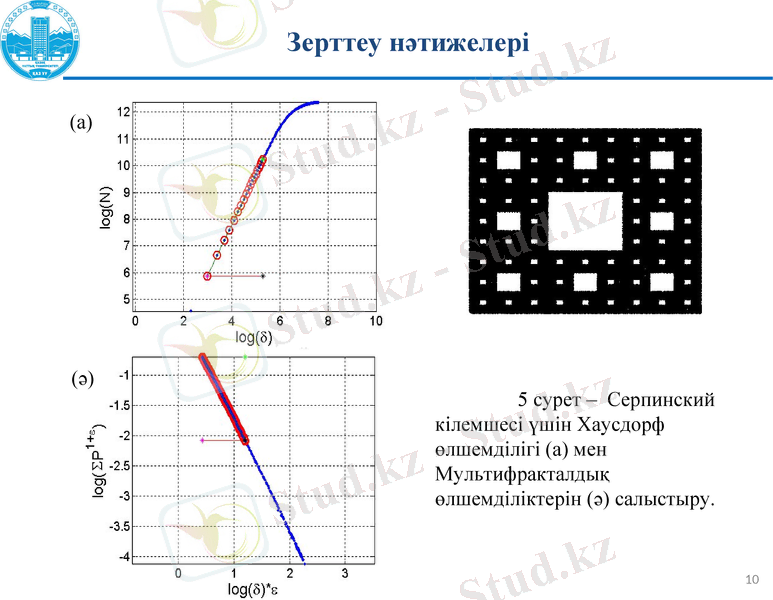
5 сурет - Серпинский кілемшесі үшін Хаусдорф өлшемділігі (а) мен Мультифракталдық өлшемділіктерін (ә) салыстыру.

(а)

(ә)

Зерттеу нәтижелері

(а)

(ә)

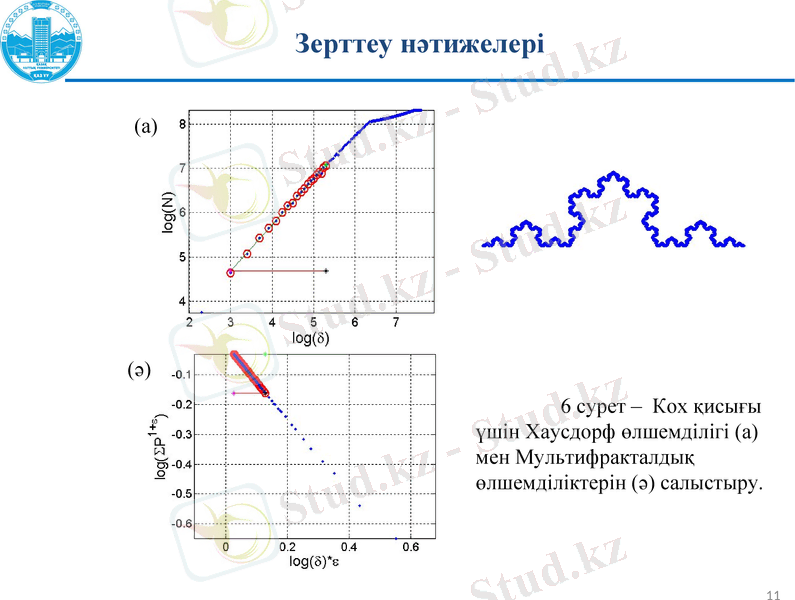
6 сурет - Кох қисығы үшін Хаусдорф өлшемділігі (а) мен Мультифракталдық өлшемділіктерін (ә) салыстыру.

Зерттеу нәтижелері

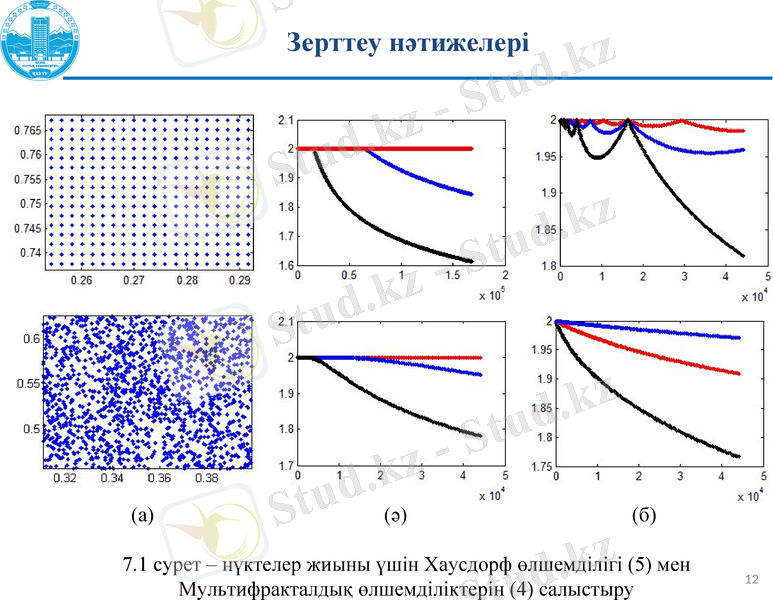
(а) (ә) (б)

7. 1 сурет - нүктелер жиыны үшін Хаусдорф өлшемділігі (5) мен Мультифракталдық өлшемділіктерін (4) салыстыру

Зерттеу нәтижелері

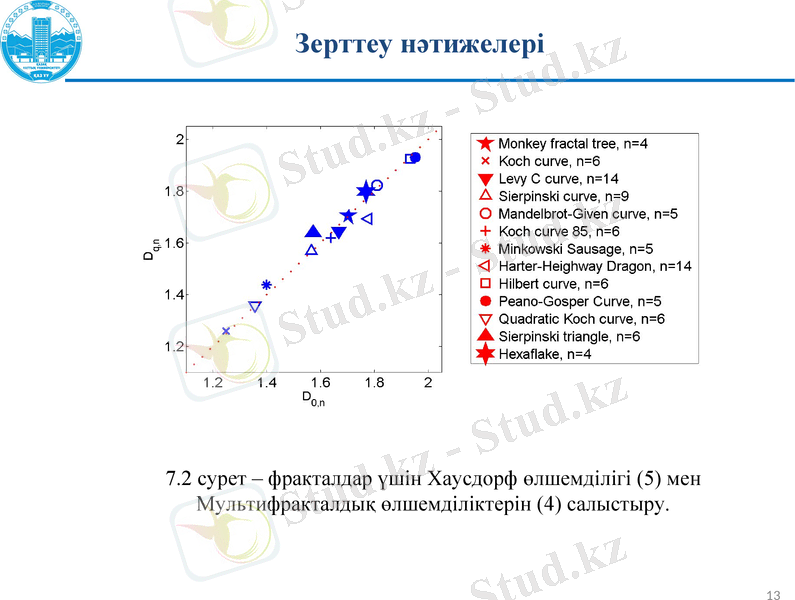
7. 2 сурет - фракталдар үшін Хаусдорф өлшемділігі (5) мен Мультифракталдық өлшемділіктерін (4) салыстыру.

Зерттеу нәтижелері

(а)

(б)

(ә)

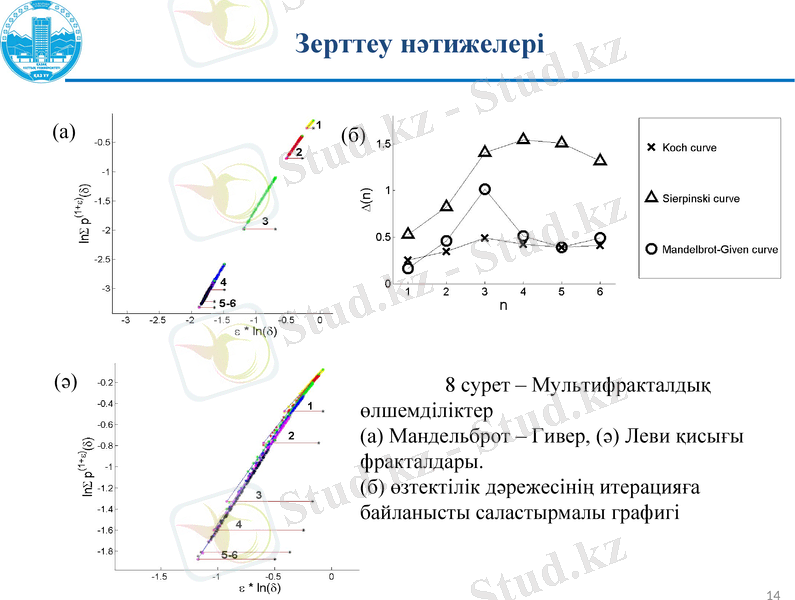
8 сурет - Мультифракталдық өлшемділіктер

(а) Мандельброт - Гивер, (ә) Леви қисығы фракталдары.

(б) өзтектілік дәрежесінің итерацияға байланысты саластырмалы графигі

Зерттеу нәтижелері

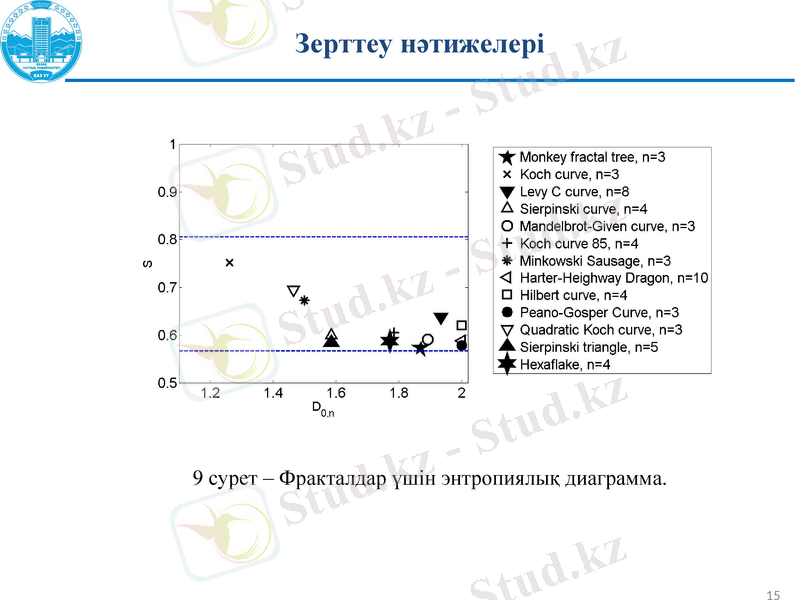
9 сурет - Фракталдар үшін энтропиялық диаграмма.

Үш өлшемді бейнелеу

(1)

(2)

Жанабаев З. Ж. и Ахтанов С. Н., Универсальное отображение перемежаемости, Вестник КазНУ, серия физическая №2 (37) 2011, с. 15-25

Zeinulla Zh. Zhanabaev, Yeldos T. Kozhagulov A generic model for scale - invariant neuron networks \\ Journal of Neuroscience and Neuroengineering, - 2013

мұндағы xi, yi-аддитивті физикалық өлшемдер, γ- xi фракталдық өлшемділіктің бөлшектік бөлігі, 1/C-бақылаудың дәлдігі (сигнал базасы), 𝜇𝑖- мультипликатор.

Модельдеу нәтижелері

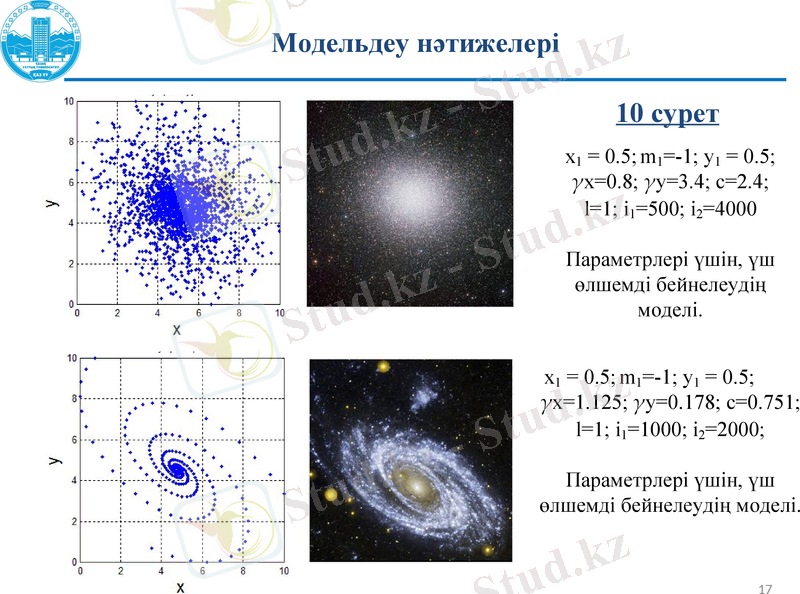
10 сурет

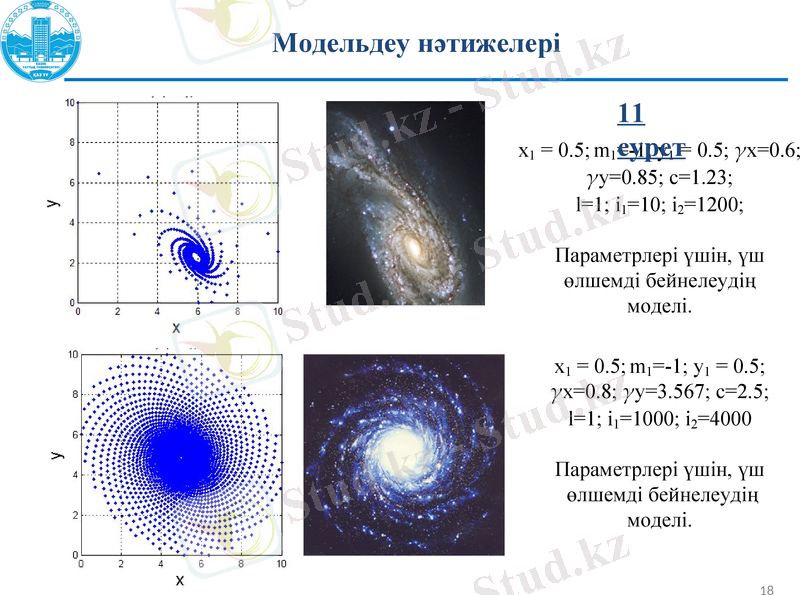
Модельдеу нәтижелері

11 сурет

Зерттеу нәтижелері

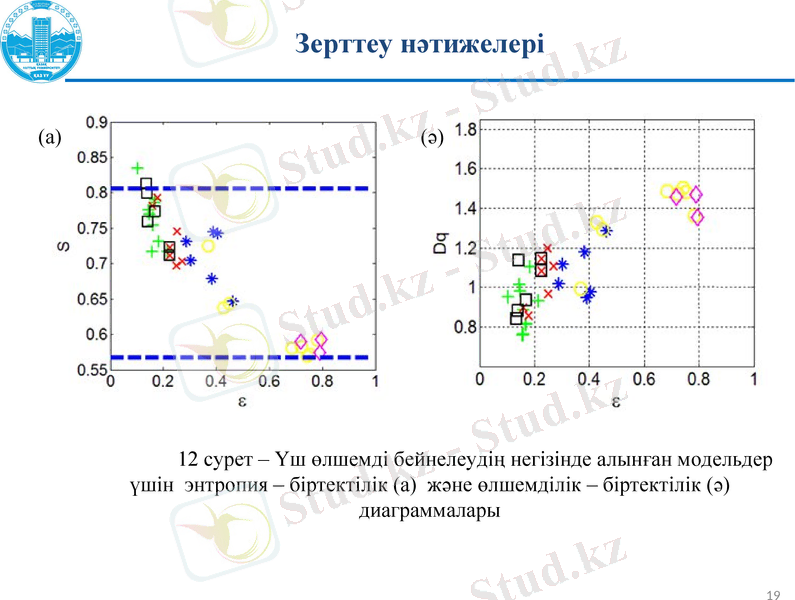
12 сурет - Үш өлшемді бейнелеудің негізінде алынған модельдер үшін энтропия - біртектілік (а) және өлшемділік - біртектілік (ә) диаграммалары

(а)

(ә)

Зерттеу нәтижелері

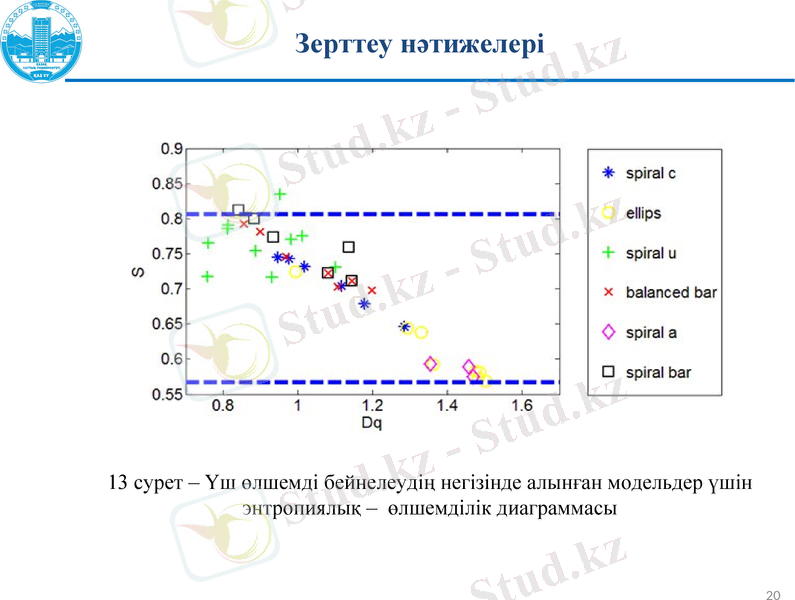
13 сурет - Үш өлшемді бейнелеудің негізінде алынған модельдер үшін энтропиялық - өлшемділік диаграммасы

Қорытынды

Бұл жұмыста алғаш рет клеткалық ақпараттық энтропияның нормасы анықталды. Екі өлшемді объектілердің энтропиясының нормасы ретінде сол объектінің Реньи энтропиясы екені тағайындалды. Хаусдорф өлшемділігін есептеудің сандық әдісін қолдана отырып, Мультифракталдық өлшемдікті тікелей эксперименттен анықтау мүмкіндігі ашылды.

Иерархиялы өзұқсас күрделі объектілер ұсынылған әдіс бойынша есептелді. Бүл әдіс көп өлшемді Шеннон энтропиясын сол объектінің Реньи энтропиясына нормалауды көздейді. Реньи энтропиясын есептеу барысында әр объектінің өзіндік қасиеті ескеріледі және сол объектінің мультифракталдық өлшемділігінің ерекшеліктері қарастырылады.

Ұқсас жұмыстар

Материя күрделі құрылым

1-модуль. Галактика модельдерін түзу. Галактиканың спиралдық құрылымы

ӘЛЕМ ҚҰРЫЛЫСЫ МЕН ЭВОЛЮЦИЯСЫ

Растрлық графика

Оқушылардың компьютерлік графикамен жұмыс

Қүн жүйесінің алғашқы ұғымдары

Галактикалар жүйесі

Цифрлық бейнелеу технологиясын дамыту тенденциялары

Бірінші жұлдыздардың пайда болуы

Ғарыштың зерттеулерғарышта заттық құрамы

Пәндер