Электр зарядының сақталу заңы

Презентация қосу

Электр зарядының
сақталу заңы
Электр заряды — релятивистік инвариантты өлшем бірлік, яғни
санақ жүйесіне тәуелсіз, ол дегеніміз зарядтың қозғалысына немесе
тыныштық күйіне тәуелсіз.

Зерттеу жұмыстарында (1910—1914)
американдық физик Р. Милликен
(1868—1953) электр зарядының
дискретті, яғни кез келген дененің
заряды е (е=1,6∙10-19 Кл) элементар
электр зарядынан тұратынын
көрсетті. Электрон (me=9,11∙10-31 кг)
және протон (mp=1,67∙10-27 кг)
сәйкесінше оң және теріс элементар
зарядтарды тасушы болып
табылады.
Зерттеу жұмыстардың нәтижесінде
фундаменталды табиғат заңы
ашылды 1843ж. ағылшын физигі М.
ашылды,
Фарадеем (1791—1867) тәжірибе
жүзінде электр зарядының сақталу
заңын тұжырымдады: кез келген
тұйық жүйеде (қоршаған денелермен
өзара әрекеттеспейтін денелер
жүйесі), осы жүйеде қандай процесс
жүріп жатқанына қарамастан, барлық
бөлшектер зарядтарының алгебралық
қосындысы өзгеріссіз қалады .

Электр зарядының өлшем бірлігі (туынды бірлік, себебі ток к үшіні ң
бірлігі арқылы анықталады) — кулон (Кл) — бұл ток күші 1 А
болғанда, өткізгіштің көлденең қимасынан 1 с уақытта өтетін электр
заряды.
Электростатикалық өріс.
Электростатикалық өрістің
кернеулігі.
Берілген нүктедегі
Электростатикалық өрістің Вакуумдағы нүктелік заряд өрісінің
кернеулігі өрістің осы кернеулігі
нүктесінде орналасқан
бірлік оң зарядқа әсер 1 Q r 1 Q
ететін күшпен анықталатын
E немесе E 2
.
4 0 r 2 r 4 0 r
физикалық шама болып
табылады.
Е векторының бағыты сол өрістегі оң зарядқа әсер
E F / Q0 ететін күштің бағытымен сәйкес келеді. Егер өріс
оң зарядтан туса, онда Е векторы радиус-
вектордың бойымен зарядтан сыртқы ортаға
бағытталады (оң зарядтан тебіледі); егер өріс теріс
зарядтан туса, онда Е векторы зарядқа қарай
бағытталады.
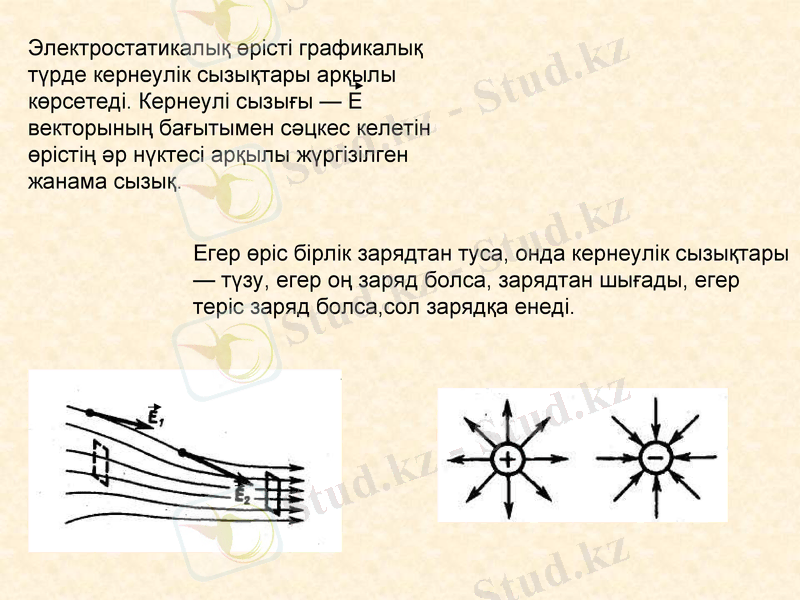
Электростатикалық өрісті графикалық
түрде кернеулік сызықтары арқылы
көрсетеді. Кернеулі сызығы — Е
векторының бағытымен сәцкес келетін
өрістің әр нүктесі арқылы жүргізілген
жанама сызық.

Егер өріс бірлік зарядтан туса, онда кернеулік сызықтары
— түзу, егер оң заряд болса, зарядтан шығады, егер
теріс заряд болса,сол зарядқа енеді.
Е векторымен α бұрыш жасайтын n нормалы
бар элементар dS ауданын қиып өтетін кернеулік
сызығының саны ЕdScosα=EndS тең, мұндағы Еn
— dS ауданындағы Е векторының n нормальға
проекциясы.

dФЕ Е n dS EdS
шамасы dS ауданы арқылы өтетін кернеулік
векторының ағыны деп аталады. Мұндағы
dS=dSn — модулі dS-қа тең вектор, ал бағыты dS dSn
ауданға түсірілген n нормальдың бағытымен
сәйкес келеді.
Е векторының ағыны кез келген тұйық S жазықтықты
қиып өтеді.

ФЕ ЕndS EdS ,
s s

Электростатикалық өрістің
суперпозиция принципі.
Дипольдің өрісі
Суперпозиция принципі кез келген қозғалмайтын
зарядтар жүйесінің электростатикалық өрісін есептеуге
мүмкіндік береді, себебі егер зарядтар нүктелік болмаса,
онда оларды әрақшан нүктелік зарядтар жиынтығына
келтіруге болады.

n
E Ei
i 1
Электрлік диполь — өрістің қарастырылып отырған
нүктелердің арақашықтығынан әлденеше кіші L
арақашықтықта орналасқан модулі жағынан тең әраттас
нүктелік (+Q, —Q) зарядтар жүйесі.

pý Q l

-Q l +Q p
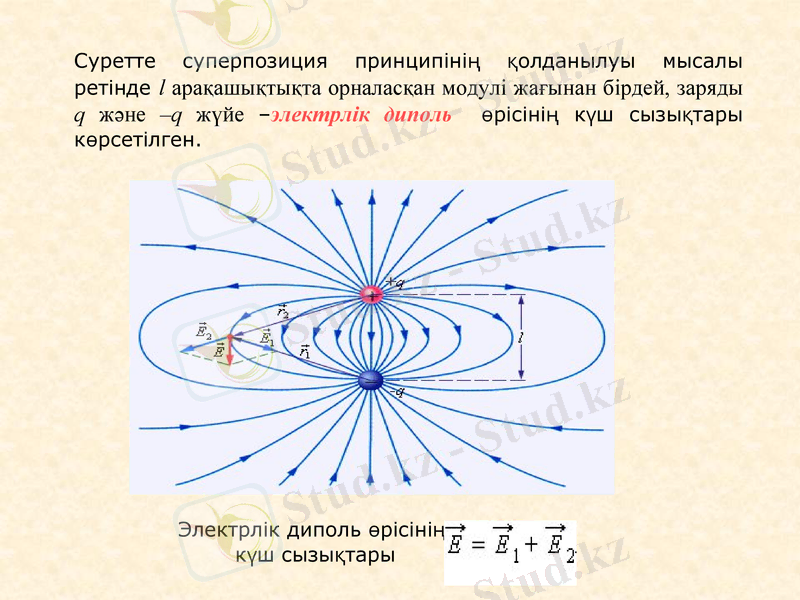
Суретте суперпозиция принципінің қолданылуы мысалы
ретінде l арақашықтықта орналасқан модулі жағынан бірдей, заряды
q және –q жүйе –электрлік диполь өрісінің күш сызықтары
көрсетілген.

Электрлік диполь өрісінің
күш сызықтары
Вакуумдағы электростатикалық
өріс үшін Гаусс теоремасы
К. Гаусса (1777—1855) теоремасы кез келген тұйық жазықтық
арқылы өтетін злектр өрісінің кернеулік векторының ағынын
анықтайды.

Тұйық және нүктелік Q зарядтан тұратын кез
келген формадағы жазықтық үшін Е векторы Q/ε0

тең болады, яғни
ФE EdS E n dS Q / 0
S S

Ағынның таңбасы Q зарядының
таңбасымен сәйкес келеді.
Гаусса теоремасын мына түрде жазуға болады:

Ed S
E n dS
0 V
dV .
S S
Кейбір вакуумдағы
электростатикалық өрістерді
есептеу үшін Гаусс теоремасын
қолдану.
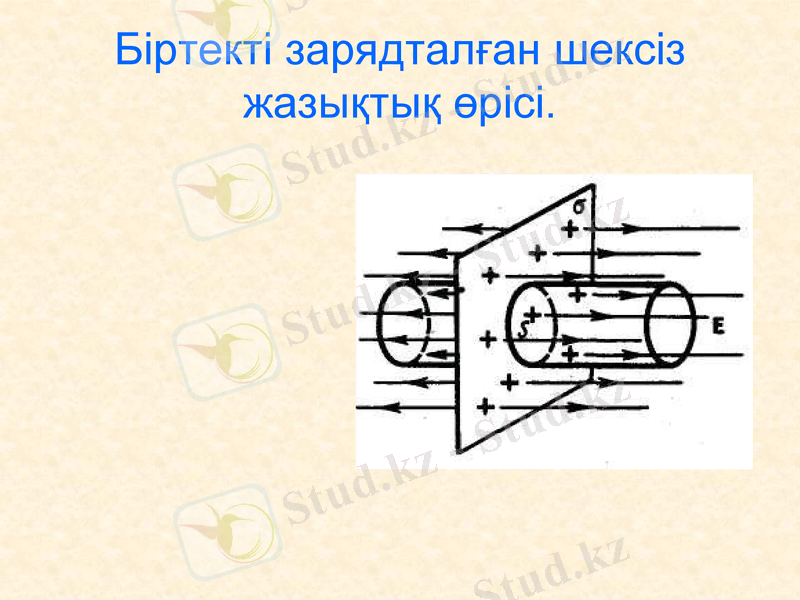
Біртекті зарядталған шексіз
жазықтық өрісі.

E n / 2 0
E 0
E
Dn / 2
D 0
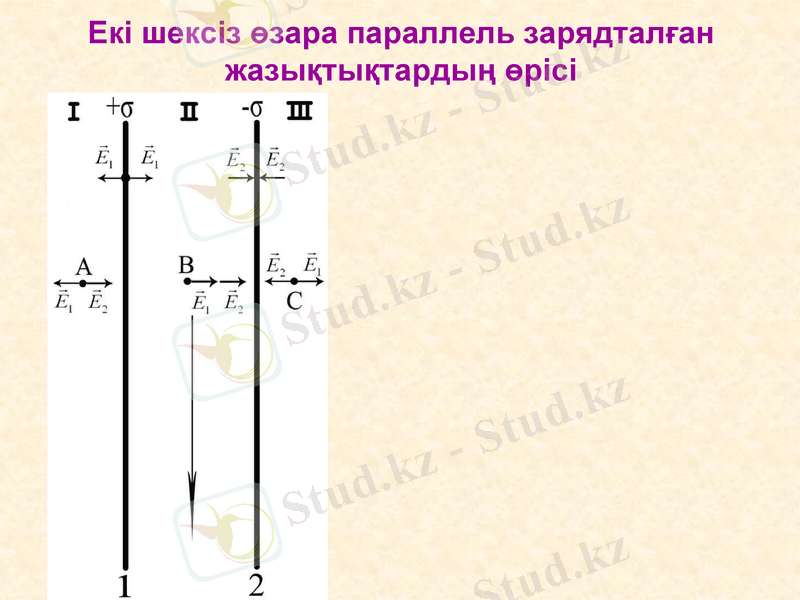
Екі шексіз өзара параллель зарядталған
жазықтықтардың өрісі

E1 E 2 , E A E1 E 2
2 0
E A E1 E2 0

EС E1 E 2
EС E1 E2 0

E В E1 E 2

E В E1 E 2 2
2 0 0
E В / 0 DВ
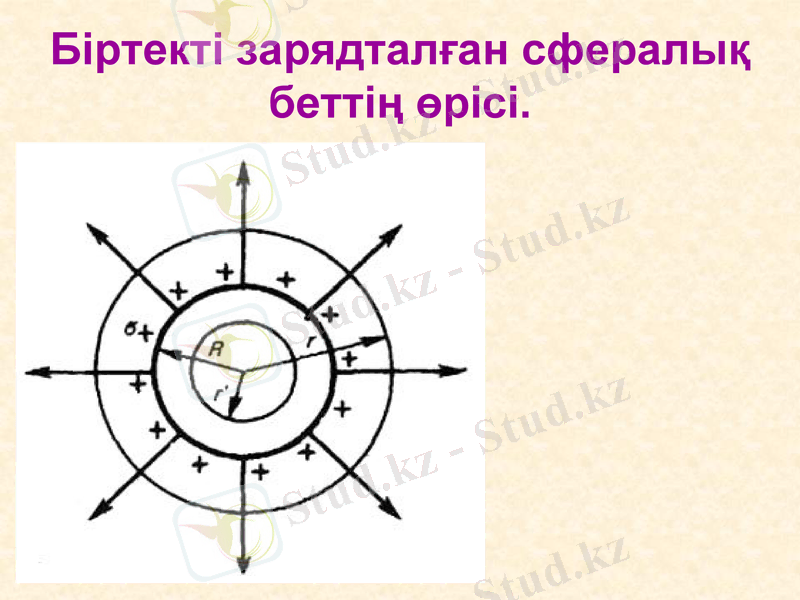
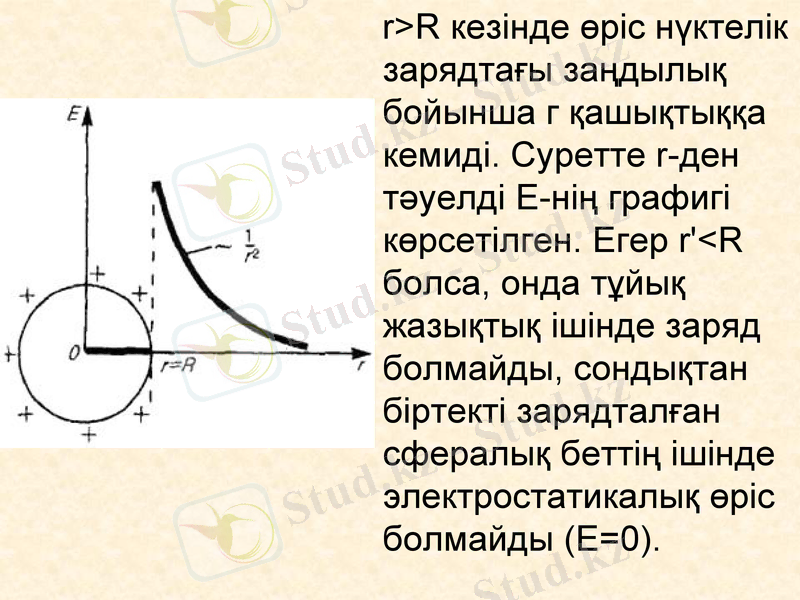
Біртекті зарядталған сфералық
беттің өрісі.

1 Q
E 2
4 0 r
E
(r R)
r>R кезінде өріс нүктелік
зарядтағы заңдылық
бойынша г қашықтыққа
кемиді. Суретте r-ден
тәуелді Е-нің графигі
көрсетілген. Егер r'болса, онда тұйық
жазықтық ішінде заряд
болмайды, сондықтан
біртекті зарядталған
сфералық беттің ішінде
электростатикалық өріс
болмайды (Е=0).
Біртекті зарядталған шексіз
цилиндр өрісі.

E ( r R )
2 0 r
Егер r жазықтықта заряд
болмайды, сондықтан
бұл кезде E=0.
Потенциалдық өрісте (электростатикалық өріс
потенциалдық болып табылады) орналасқан,
зарядталған дене өріс күшімен істелетін жұмысқа
кететін потенциалдық энергияға ие болады.
Потенциалдық энергияның кемуінің арқасында
консервативті күштердің жұмысы атқаратыны белгілі.
Сондықтан электростатикалық өріс күшінің жұмысын
Q зарядының өрісінің бастапқы және соңғы
нүктелеріндегі Q0 нүктелік зарядтың потенциалдық
энергиясының айырымы ретінде көрсетуге болады :

1 QQ0 1 QQ0
A12 U1 U 2 .
4 0 r1 4 0 r2
1 нүктесінен 2 нүктесіне орын ауыстырған Q0
зарядтың өріс күшінің жұмысы мына түрде де жазыла
алады:
A12=U1- U2=Q0(φ1 - φ2).
1 нүктесіне 2 нүктесіне электростатикалық өріс күшінің
әсерінен орын ауыстырған Q0 зарядтың жұмысы мына
түрде беріле алады:

A12=U1- U2=Q0(φ1 - φ2),

яғни бастапқы және соңғы нүктелердегі
потенциалдарының айырмасын орын ауыстырған заряд
шамасына көбейткенге тең. Электр өрісінің 1 және 2
нүктелерінің потенциалдарының айырмасы бірлік оң
зарядтың өріс күшінің әсерінен 1 нүктесінен 2 нүктесіне
орын ауыстырғанда істелетін жұмыс шамасымен
анықталады.
Сонымен қатар 1 нүктесіне 2
нүктесіне электростатикалық өріс
күшінің әсерінен орын ауыстырған
Q0 зарядтың жұмысы мына түрде
беріле алады :

A12 Q0 Edl .
Бағытталған электростатикалық өрістің
кернеулік векторының циркуляциясы:

Ц Е ( Е dl ) 0
l

F 1 1 1
Ц Е

q

dl
q
F dl dA
ql qпроб .
Q0 1 2
l проб . проб . l

1 2 Ц Е 0 l

dl

E
Электр өрісінің кернеулігі мен
φ потенциал арасындағы
байланыс.

E grad
Декарттық координат жүйесінде:

E i j k
x y z
Егер өріс біртекті және Х осі
бойымен бағытталса, онда:

E i
x
ДӘРІСТІҢ СОҢЫ

Ұқсас жұмыстар

Дененің электр заряды оның құрамына енетін барлық бөлшектің Электр зарядының алгебр

Электродинамика. Электр құбылыстары

Электр құбылыстары тұрмыста

Электр заряды және электр өрісі

Атом құрылысы

Электр заряды Нүктелік заряд Жаңа сабақ

Есептер жинағынан есептер шығару

Кирхгоф ережелері

Конденсаторлар

Заттың агрегаттық күйлері

Пәндер