Екі айнымалы теңдеулер мен жүйелері, теңсіздіктер және сандар тізбегі: түрлері, беру тәсілдері және есептер

1. Екі айнымалысы бар теңдеу

2. Теңдеулер жүйесі

3. Бір айнымалысы бар теңсіздіктер

4. Олардың жүйелері

5. Екі айнымалысы бар теңсіздіктерді шешу

6. Теңсіздіктерді дәлелдеу

Өткен тарауда нені игердік ?

Сабақтың тақырыбы:

Сандар тізбегі және

олардың берілу тәсілдері.

Сандар тізбегі, мүшелері.

Мысалы, натурал сандарды

1-ден бастап жазып шықсақ,

1; 2; 3; 4; 5; 6; 7; . . .

сандар тізбегі шығады.

Немесе 2; 4; 6; 8; 10; . . .

онда жұп сандар тізбегі пайда болды, әрқайсысын белгілесек,

а1 а2 а3 а4 а5

а6=12; а15=30; . . . аn=2n

Натурал аргументті функция сандар тізбегі,

ал тізбекті құрайтын сандарды тізбектің мүшелері

деп атайды.

Анықтама:

Баяндау тәсілі

Берілу тәсілдері

Сандар тізбегі

Аналитикалық тәсіл

Рекурренттік тәсіл

Графиктік тәсіл

график арқылы беріледі

келесі мүше алдыңғы мүше арқылы анықталады

формула арқылы беріледі

сөзбен беріледі

Тізбектің түрлері:

Шекті

Шексіз

Өспелі

Кемімелі

Тұрақты

Есептер шығару

Екі топқа бөліп жарысу

1- топ 2- топ

Х тобы У тобы

№148(а) №148(б)

27; 9; 3; 1; . . .

ІІ

103; 95; 87; 79; . . .

Тізбекті жалғастыр

№ 149(а) № 149(б)

Тізбекті жалғастыр да,

қарапайым формуласын көрсет.

1; 1/2; 1/3; 1/4; . . . 2/3; 3/4; 4/5; 5/6; . . .

-8; -5; -2; 1; 4; . . . -1; -2; -3; -4; . . .

№ 150

Тізбек өспелі ме?

Егер тізбек аn = 2п3 -3п формуласымен берілсе,

оның екінші мүшесін табыңыз.

А) 10 В) 12 С) 15 Д) 16 Е) 20

2. Тізбектің үшінші мүшесін тап: аn= П 3+1

А) 1 В) 14 С) 2 Д) 28 Е) 7

3. аn = п2 - п тізбегінің тоғызыншы мүшесін табыңыз.

А) 49 В) 80 С) 27 Д) 77 Е) 72

4. аn = 3п +2 болса бесінші мүшесі нешеге тең?

А) 15 В) 16 С) 17 Д) 18 Е) 20

Тест тапсырмалары

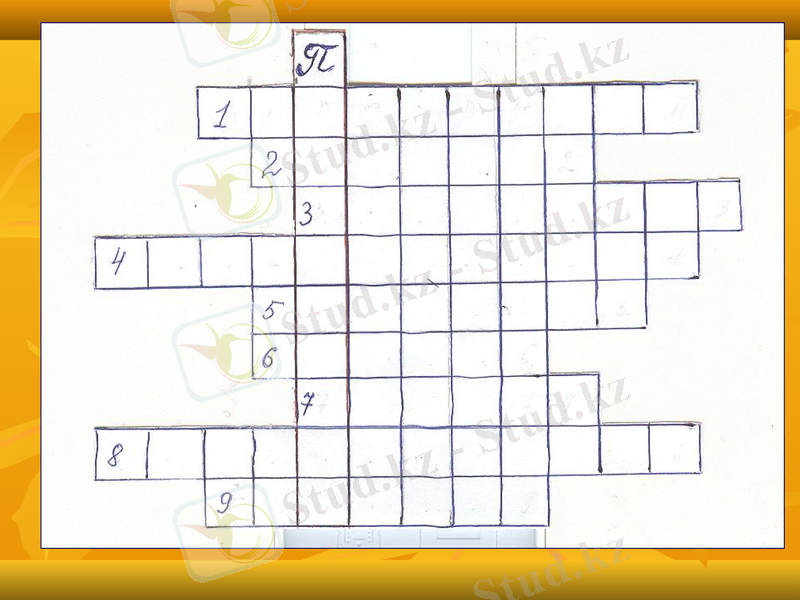
Сөзжұмбақты дұрыс шешкенде, П әрпінен басталатын алгебра курсындағы ең негізгі тізбектердің атауын оқисыз.

1. Өспелі және кемімелі тізбектер.

2 Аналитикалық тәсіл деген не?

3. Координаталық жазықтық арқылы анықталатын тәсіл.

4. Келесі мүшесі алдыңғы мүше арқылы анықталатын тәсіл.

5. 1; 1/2; 1/3; 1/4; 1/5; . . . қандай тізбек?

6. 2; 4; 6; 8; . . . қандай тіздек?

7. Тізбек неден тұрады?

8. п -ші мүшесі формуламен берілсе, қандай тәсіл?

9. Сандардың орналасу заңдылығы сөзбен берілетін тәсіл.

СӨЗЖҰМБАҚ

Үйге тапсырма:

ІІ тарау, § 9.

№ 152, 154, 158-есептер

Сабақ аяқталды.

Ұқсас жұмыстар

Квадрат теңдеулер: анықтама, түрлері және есептер

Квадраттық теңдеулер: анықтамалар, түрлері және есептер

Рационал сандар: салыстыру, теңсіздіктер және модульдік тапсырмалар

Сандар тізбегі және арифметикалық прогрессия: анықтамасы, негізгі қасиеттері және қолданылуы

Логарифмдік теңдеулер және оларды шешу тәсілдері (11-сынып алгебрасы)

Квадрат теңдеулер: анықтамалар, түрлері және практикалық есептер

Квадраттық теңсіздіктер мен парабола графиктері бойынша есептер

Квадрат теңдеулер: түрлері, дискриминант, түбірлер және практикалық есептер

Сызықтық теңдеулер жүйелері және олардың классификациясы: матрицалық жазылуы және Крамер ережесі

1-сынып математикасы: Бір таңбалы және екі таңбалы сандар - сабақ жоспары

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz