Квадраттық теңдеулерді формула арқылы шешу: алгоритм, дискриминант және жаттығулар

Скачать

Сабақтың тақырыбы: Квадраттық теңдеулерді формула арқылы шешу

Сабақтың мақсаты:

Білімділік:Квадраттық теңдеуді шешуде формулаларды тиімді пайдалану дағдыларын қалыптастыру

Дамытушылық: Ойлау қабілеттерін, өз беттерімен жұмыс жасауын дамыту, математикаға деген қызығушылығын арттыру.

Тәрбиелік: Алған білімдеріне жауапкершілікпен қарауға, өз мүмкіндігіне сенуге, үлкен жетістікке ұмтылуға үйрету.

Анаграмма

Таиимдкисрнн

ңеетду

фэкоцинетиф

үртіб

Ответы:

Квадратық теңдеулерді шешу

Сабақтың тақырыбы:

Сабағымыздың ұраны:

Мен білемін, мен үйренемін

Өзіңді тексер

Теңдеу

толымды

толымсыз

келтірілген

келтірілмеген

Толық балл

Квадраттық теңдеуді шешу алгоритмі

Квадраттық теңдеудің түбірлері және дискриминант

D=b2-4ac

D>0

Теңдеудің екі түбірі бар

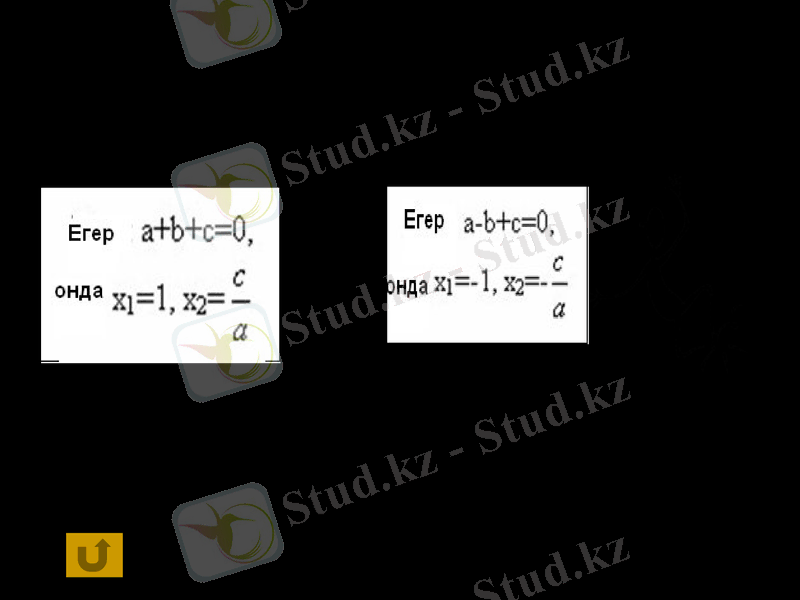
Қосымша формулалар

Өзіндік жұмыс

а)

б)

1 нұсқа

2 нұсқа

в)

г)

Түбірі жоқ

1; 1, 5

-1; 1, 5

-1; 3

1; 0, 6

1; -3

-1; -2

и

х

м

с

а

н

и

1-нұсқа

Теңдеу

Коэффициенттер-дің қосындысы

а + в + с

Түбірлер

2 - 5 + 3 = 0

5 - 8 + 3 = 0

а + в + с = 0

Теңдеу

а - в + с

Түбірлері

1 - (- 2) +(- 3) = 0

1 - 3 + 2 = 0

а - в + с = 0

2-нұсқа

Теңдеудің түбірі болатын үлкен санды тап

Жауап: 1.

Назарларыңызға рақмет!

Өзіңді тексер

Теңдеу

толымды

толымсыз

келтірілген

келтірілмеген

Толық балл

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс