Екілік санау жүйесі

Екілік санау жүйесінде сандарды алу

Екілік санау жүйесінде сандарды қосу

Екілік жүйедегі санның ондық жүйедегі эквивалентін табу

Ондық жүйедегі санның екілік жүйедегі эквивалентін табу

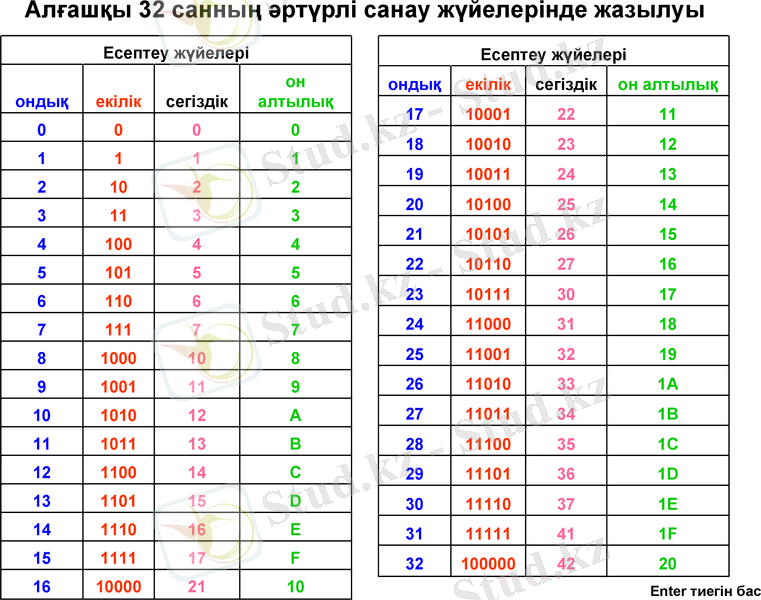
Алғашқы 32 санның әртүрлі санау жүйелерінде жазылуы

Санау жүйелерінің түрлері

Санау жүйелері. Екілік санау жүйесі.

Екілік санау жүйесінде сандарды көбейту және бөлу

Enter тиегін бас

Ондық санау жүйесінде (біздің күнделікті есептеуде қолданатын жүйеде) санды көрсету үшін 10 арап цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - қолданылады

Мысалы: қырық үш бүтін жүзден сексен екі ондық есептеу жүйесінде жазылады

43, 82

Екілік санау жүйесінде санды көрсету үшін 2 арап цифры: 0, 1 - қолданылады

Мысалы: қырық үш бүтін жүзден сексен екі екілік есептеу жүйесінде жазылады

≈ 101011, 11011

Сегіздік санау жүйесінде санды көрсету үшін 8 арап цифры: 0, 1, 2, 3, 4, 5, 6, 7 - қолданылады

Мысалы: қырық үш бүтін жүзден сексен екі сегіздік есептеу жүйесінде жазылады

≈ 53, 64365

Он алтылық санау жүйесінде санды көрсету үшін 10 арап цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 және 6 латын әріптері A, B, C, D, E, F қолданылады

Мысалы: қырық үш бүтін жүзден сексен екі он алтылық есептеу жүйесінде жазылады

≈ 2B, D05B7

Санау жүйелерінің түрлері

Санның қандай санау жүйесінде жазылғанын білдіру үшін санау жүйесі белгісі индекс түрінде қойылады:

43, 8210 ≈ 101011, 110112 ≈ 53, 643658 ≈ 2B, D05B716

Enter тиегін бас

Есептеу жүйелері

ондық

екілік

сегіздік

он алтылық

100

101

110

111

1000

1001

1010

1011

1100

1101

1110

Есептеу жүйелері

ондық

екілік

сегіздік

он алтылық

10001

10010

10011

10100

10101

10110

10111

11000

11001

11010

11011

11100

11101

Алғашқы 32 санның әртүрлі санау жүйелерінде жазылуы

Enter тиегін бас

1) 357 санын 2-ге бүтінге дейін дәлдікпен бөлсе нәтиже 178 болады да, 1 қалдық қалады (қызыл түспен көрсетілген)

2) 178 санын 2-ге бүтінге дейін дәлдікпен бөлсе нәтиже 89 болады, қалдық қалмайды, сондықтан қалдыққа 0 жазылады (қызыл түспен көрсетілген)

3) 89 санын 2-ге бүтінге дейін дәлдікпен бөлсе нәтиже 44 болады да, 1 қалдық қалады (қызыл түспен көрсетілген)

4) 44 санын 2-ге бүтінге дейін дәлдікпен бөлсе нәтиже 22 болады, қалдық қалмайды, сондықтан қалдыққа 0 жазылады (қызыл түспен көрсетілген)

5) 22 санын 2-ге бүтінге дейін дәлдікпен бөлсе нәтиже 11 болады, қалдық қалмайды, сондықтан қалдыққа 0 жазылады (қызыл түспен көрсетілген)

6) 11 санын 2-ге бүтінге дейін дәлдікпен бөлсе нәтиже 5 болады да, 1 қалдық қалады (қызыл түспен көрсетілген)

7) 5 санын 2-ге бүтінге дейін дәлдікпен бөлсе нәтиже 2 болады да, 1 қалдық қалады (қызыл түспен көрсетілген)

8) 2 санын 2-ге бүтінге дейін дәлдікпен бөлсе нәтиже 1 болады, қалдық қалмайды, сондықтан қалдыққа 0 жазылады (қызыл түспен көрсетілген)

9) 1 санын 2-ге бүтінге дейін дәлдікпен бөлсе нәтиже 0 болады да, 1 қалдық қалады (қызыл түспен көрсетілген)

Ондық есептеу жүйесіндегі 357, 79 санын екілік есептеу жүйесіндегі санға айналдыру

Бөлу амалы 1-ді 2-ге бөлу әрекеті орындалғанға дейін жүргізіледі

35710 = 1011001012

үшін оның бүтін бөлігіне 2-ге бөлу, бөлшек бөлігіне 2-ге көбейту қолданылады

Eкілік жүйедегі эквивалент үшін қалдықтар тізбегі соңғысынан ал-ғашқыға (төмен-нен жоғары) қарай алынады

Ондық жүйедегі санның бөлшек бөлігінің екілік жүйедегі эквивалентін табу үшін санның тек бөлшек бөлігі 2-ге көбейтіледі.

1) 0, 79 санын 2-ге көбейтсе 1, 58 саны шығады. 0, 79 бен 1, 58-дің бүтін бөліктері бөлектеніп ерекше жазылды (қызыл түспен көрсетілген)

2) Шыққан нәтиженің (1, 58) бөлшек бөлігі 0, 58-ді 2-ге көбейтсе 1, 16 болады. 1, 16-ның бүтін бөлігі бөлектеніп жазылды (қызыл түспен көрсетілген)

3) Шыққан нәтиженің (1, 16) бөлшек бөлігі 0, 16-ны 2-ге көбейтсе 0, 32 болады. 0, 32-ның бүтін бөлігі бөлектеніп жазылды (қызыл түспен көрсетілген)

4) Шыққан нәтиженің (0, 32) бөлшек бөлігі 0, 32-ні 2-ге көбейтсе 0, 64 болады. 0, 64-тің бүтін бөлігі бөлектеніп жазылды (қызыл түспен көрсетілген)

5) Шыққан нәтиженің (0, 64) бөлшек бөлігі 0, 64-ті 2-ге көбейтсе 1, 28 болады. 1, 28-дің бүтін бөлігі бөлектеніп жазылды (қызыл түспен көрсетілген)

Санның екілік жүйеде көрсетілу дәлдігі, яғни үтірден кейінгі орын, белгілі болуы керек

Көбейту кезінде шығатын шамалардың бүтін бөлігі бөлек жазылады, олар екілік эквивалентті береді.

0, 79-дың екілік жүйедегі эквивалентін 5 орынға дейінгі дәлдікпен табу үшін келесі амалдарды орындау керек:

0, 7910 = 0, 110012

357, 7910 = 101100101, 110012

Бүтіндер жиынтығы жоғарыдан төмен қарай бөлшек бөлік ретінде алынады

Ондық жүйедегі санның екілік жүйедегі эквивалентін табу

Enter тиегін бас

101100101, 110012

Разряд 8 7 6 5 4 3 2 1 0

Екілік жүйедегі 101100101, 11001-дің ондық жүйедегі эквивалентін табу

үшін осы сандағы әрбір цифрға (бір мен нөлдерге) бүтін сан түріндегі разряд беріледі.

Үтір алдындағы цифрға 0-ге тең разряд беріледі және ол солға қарай артады, оңға қарай кемиді. Разряд бүтін бөлік үшін оң, бөлшек бөлік үшін теріс таңбалы болады :

Екілік санау жүйесіндегі санның әрбір цифрының осы цифрдың разрядындағы екінің дәрежесіне көбейтінділерінің қосындылылары осы санның ондық жүйедегі эквивалентін береді:

1*28+0*27+1*26+1*25+0*24+0*23+1*22+0*21+1*20+1*2-1+1*2-2+0*2-3+0*2-4+1*2-5=

= 256 + 0 + 64 + 32 + 0 + 0 + 4 + 0 + 1 + 0, 5 + 0, 25 + 0 + 0 + 0, 03125 =

= 357, 78125

-1

-2

-3

-4

-5

256

128

0, 5

0, 25

0, 125

0, 0625

0, 03125

Осы есептеуде қолданылған екінің әртүрлі дәрежесінің мәні

101100101, 110012 357, 7910 санының екілік санау жүйесіндегі эквиваленті ретінде анықталған болатын, ендеше екілік жүйедегі эквивалент ондық жүйедегі санға жуық (тең не кіші) шама болады.

Екілік жүйедегі санның ондық жүйедегі эквивалентін табу

-1 -2 -3 -4 -5

Enter тиегін бас

Екілік санау жүйесінде сандарды қосу

Екілік санау жүйесіндегі сандарды қосу амалын орындау үшін мына жағдайларды ескеру керек :

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10 нөл жазылып, бір есте сақталады

10110011, 10101 және 10110, 01110 сандарын қосуды қарастыралық

Бұл сандар бөлшек белгісі үтір бір баған бойында орналастырылып жазылады.

Қосу оңнан солға қарай бірдей разрядты цифрлар үшін жүргізіледі.

Үтірдің сол жағындағы цифрға 0-ші разряд беріледі, Одан солға қарай разряд өседі (оң таңбалы болады), оңға қарай разряд кемиді (теріс таңбалы болады) .

-5 разрядты цифрларды 1 және 0 қосқанда нәтиже 1 болады.

-4 разрядты цифрларды 0 және 1 қосқанда нәтиже 1 болады.

-3 разрядты цифрларды 1 және 1 қосқанда нәтиже 10 болады. 0 жазылып 1 келесі разрядты цифрларға қосу үшін есте сақталады (қызыл түспен көрсетілген) .

-2 разрядты цифрларды 0 мен 1 және ойдағы 1-ді қосқанда нәтиже 10 болады. 0 жазылып 1 келесі разрядты цифрларға қосу үшін есте сақталады (қызыл түспен көрсетілген) .

-1 разрядты цифрларды 1 мен 0 және ойдағы 1-ді қосқанда нәтиже 10 болады. 0 жазылып 1 келесі разрядты цифрларға қосу үшін есте сақталады (қызыл түспен көрсетілген) .

0 разрядты цифрларды 1 мен 0 және ойдағы 1-ді қосқанда нәтиже 10 болады. 0 жазылып 1 келесі разрядты цифрларға қосу үшін есте сақталады (қызыл түспен көрсетілген) .

1 + 1 + 1 = 11 бір жазылып, бір есте сақталады

1 разрядты цифрларды 1 мен 1 және ойдағы 1-ді қосқанда нәтиже 11 болады. 1 жазылып 1 келесі разрядты цифрларға қосу үшін есте сақталады (қызыл түспен көрсетілген) .

2 разрядты цифрларды 0 мен 1 және ойдағы 1-ді қосқанда нәтиже 10 болады. 0 жазылып 1 келесі разрядты цифрларға қосу үшін есте сақталады (қызыл түспен көрсетілген) .

3 разрядты цифрларды 0 мен 0 және ойдағы 1-ді қосқанда нәтиже 1 болады да, ол нәтижеге жазылады.

4 разрядты цифрларды 1 мен 1-ді қосқанда нәтиже 10 болады. 0 жазылып 1 келесі разрядты цифрларға қосу үшін есте сақталады (қызыл түспен көрсетілген) .

5 разрядты цифр 1 мен ойдағы 1-ді қосқанда нәтиже 10 болады. 0 жазылып 1 келесі разрядты цифрларға қосу үшін есте сақталады (қызыл түспен көрсетілген) .

6 разрядты цифр 0 мен ойдағы 1-ді қосқанда нәтиже 1 болады да, ол нәтижеге жазылады.

7 разрядты цифр 1 мен қосылатын цифр жоқ сондықтан оның өзі нәтижеге жазылады.

Разряд 7 6 5 4 3 2 1 0

-1 -2 -3 -4 -5

Enter тиегін бас

Екілік санау жүйесінде сандарды алу

Екілік санау жүйесіндегі сандарды алу амалын орындау үшін мына жағдайларды ескеру керек :

1) 0 - 0 = 0

2) 1 - 0 = 1

3) 1 - 1 = 0

4) 10 - 1 = 1

1010011, 10101-ден 0, 0-ді алуды қарастыралық

Бұл сандар бөлшек белгісі үтір бір баған бойында орналастырылып жазылады.

Алу оңнан солға қарай бірдей разрядты цифрлар үшін жүргізіледі.

-5 разрядты цифрларда 1-ден 0-ді алғанда (2-ші жағдай) нәтиже 1 болады.

-4 разрядты цифрларда 0-ден 1-ді алу үшін -3 разрядты 1-ді жалдау керек. Сонда -4 разрядты 0 орнында 10 болады, одан 1-ді алғанда нәтиже 1 болады (4-жағдай) . -3 разрядты 1 орнында 0 қалады.

-3 разрядты цифрларда 0-ден 1-ді алу үшін -1 разрядты 1-ді жалдау керек. Оның орнында 0 қалады. Сонда -2 разрядты 0 орнында 10 болады, одан 1-ді -3 разрядтағы 0-ге жалғанда -2 разряд цифрының орнында 1 қалады, ал -3 разряд цифрының орнында 10 болады . Одан 1-ді алғанда нәтиже 1 болады (4-жағдай) .

-2 разрядты цифрларда 1-ден 1-ді алғанда (3-ші жағдай) нәтиже 0 болады.

Ұқсас жұмыстар

Санау жүйелері: екілік, сегіздік, ондық, он алтылық

Екілік санды ондық санау жүйесіне ауыстыру

АҚПАРАТ ЖӘНЕ АҚПАРАТТЫҚ ҮДЕРІСТЕР

01012 екілік сандарды азайтыңдар

Санау жүйесі туралы ақпарат

Санау жүйесі

Екілік санау жүйесінде сандарды алу

Есептегіш туралы жалпы түсінік

Қосу амалдарын орындау

Алғашқы есептеу құралдары