Квадрат теңдеулерді шешудің әдістері: анықтама, дискриминант формуласы, мысалдар мен тарихи шолу

Квадрат теңдеулерді шешудің әр түрлі тәсілдері

Квадрат теңдеулерді формула арқылы шешу

Квадрат теңдеу анықтамасы.

Квадрат теңдеу деп ах²+вх+с=0 түріндегі теңдеуді айтады, мұндағы х - айнымалы, а, в, с - нсандар, және а≠0.

а, в, с - квадрат теңдеудің коэффициенттері. а саны- бірінші коэффициент, в - екінші коэффициент, с - бос мүше.

Егер ах²+вх+с=0 квадрат теңдеудің кем дегенде бір коэффициенті в немесе с нольге тең болса, онда ол теңдеу толымсыз квадрат теңдеу деп аталады .

Квадрат теңдеуде, егер коэффициенті а=1 болса, онда ол теңдеу келтірілген деп аталады.

Квадрат теңдеулерге мысалдар:

Мысалы: а) -х² +6х+1, 2=0, мұндағы а=-1, в=6, с=1, 2;

б) 5х² - 2=0 -толымсыз квадрат теңдеу, мұнда а=5, в=0, с=-2;

в) -3х²+7х=0 - толымсыз квадрат теңдеу, мұнда а=-3, в=7, с=0;

г) 7х²=0 - толымсыз квадрат теңдеу, мұнда а=7, в=0, с=0;

д) х²+4х-12=0 - толымсыз квадрат теңдеу, мұнда а=1, в=4, с=-12.

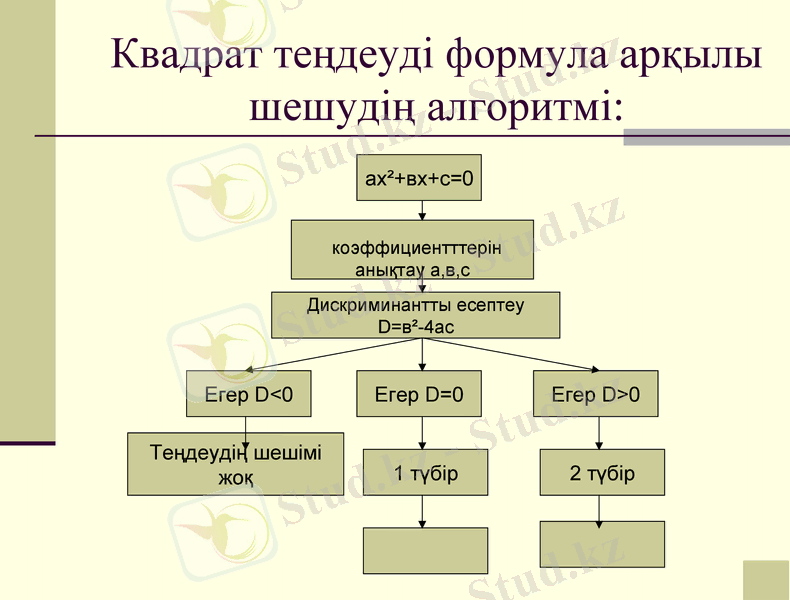
Квадрат теңдеуді формула арқылы шешудің алгоритмі:

ах²+вх+с=0

коэффициентттерін

анықтау а, в, с

Егер D<0

Дискриминантты есептеу

D=в²-4ас

Егер D=0

2 түбір

Егер D>0

1 түбір

Теңдеудің шешімі

жоқ

Квадрат теңдеулерді формула арқылы шешудің мысалдары

Мысал 1: 3х²+11х+6=0 а=3; в=11; с=6.

D=11²-4*3*6=121-72=49>0 - теңдеудің 2 түбірі бар.

Квадрат теңдеулерді формула арқылы шешудің мысалдары

Мысал 2. 9х²-6х+1=0

а=9; в=-11; с=1.

D=(-6) ²-4*9*1=36-36=0=0 - теңдеудің 1 түбірі бар.

Х=

Квадрат теңдеулерді формула арқылы шешудің мысалдары

Мысал 3: -2х²+3х-5=0

а=-2; в=3; с=-5.

D=3²-4*(-2) *5=9-40=-31<0 - теңдеудің түбірі жоқ.

Квадрат теңдеулерді шешудің тарихынан.

2-ші дәрежелі теңдеулерді шешуді б. э. д II мыңжылдықта Ежелгі Вавилонда шығара білген. Ежелгі Греция математиктері квадрат теңдеулерді геометриялық тәсілмен шешкен; мысалы, Евклид -кесіндіні орта және шеткі қатынастарға бөлу арқылы шешкен.

Квадрат теңдеудің түбірлерінің формуласы бірнеше рет «қайтадан ашылған» . Бізге жеткен деректер бойынша ең бірінші бұл формулаларды үнді математигі Брахмагупте ашқан(жуықтап 598 ж. ) .

Ортаазия ғалымы ал-Хорезми (IX . ғ) өзінің «Китаб аль-джебр валь -мукабала» трактатында бұл формуланы екімүшенің толық квадратын геометриялық интерпретация арқылы айырып алу жолымен шешкен.

Квадрат теңдеулерді шешудің тарихынан.