Туынды көмегімен функцияны зерттеу және оның графигін құрастыру



Туындының көмегімен функцияны зерттеу және оның графигін салу
Жусупова Зинеш

Сабақтың мақсаты:
Функцияны туындының көмегімен зерттеу алгоритмімен танысу
Оны қолдану арқылы функцияны зерттеу
Графигін салуды үйрену

Естігенімді - ұмытамын.
Көргенімді - есте сақтаймын.
Жасағанымды - түсінемін.
Конфуций

Өткен сабақтарға шолу

Функция туындысын тап:
1.
5.
6.
7.
8.
9.
2.
3.
4.
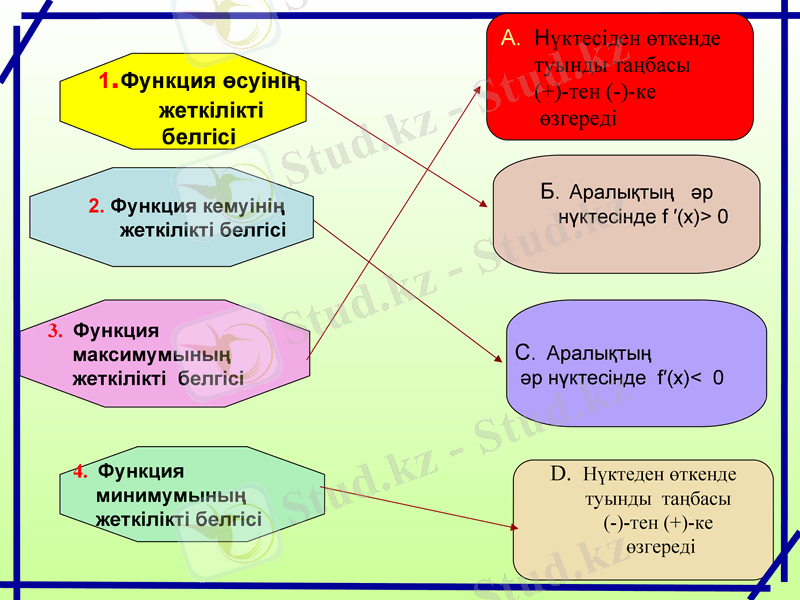
1. Функция өсуінің
жеткілікті белгісі
2. Функция кемуінің
жеткілікті белгісі
3. Функция
максимумының
жеткілікті белгісі
4. Функция
минимумының
жеткілікті белгісі
D. Нүктеден өткенде
туынды таңбасы
(-) -тен (+) -ке
өзгереді
А. Нүктесіден өткенде
туынды таңбасы
(+) -тен (-) -ке
өзгереді
Б. Аралықтың әр
нүктесінде f ′(х) > 0
С. Аралықтың
әр нүктесінде f′(х) < 0
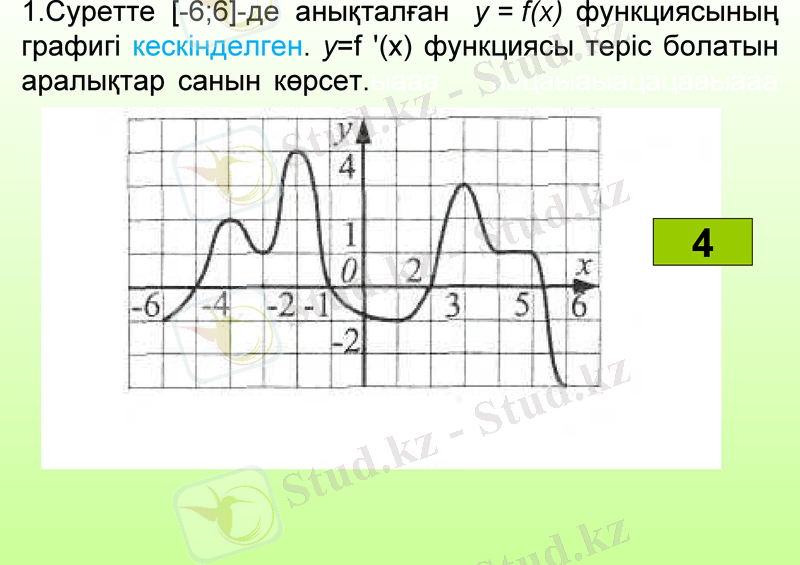
1. Суретте [-6; 6] -де анықталған функциясының графигі кескінделген. у=f '(х) функциясы теріс болатын аралықтар санын көрсет. ыааа аацаыаыацацааыааа
4
у = f(x)
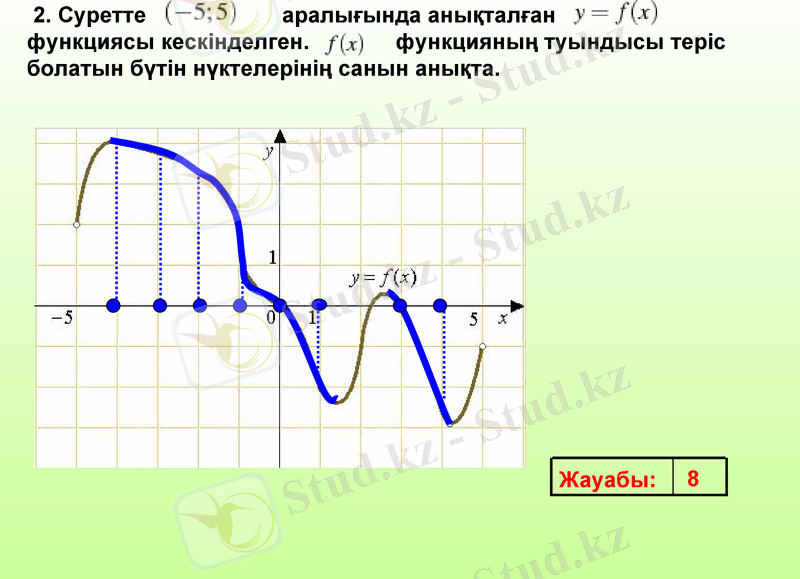
2. Суретте аралығында анықталған функциясы кескінделген. функцияның туындысы теріс болатын бүтін нүктелерінің санын анықта.
Жауабы:
8
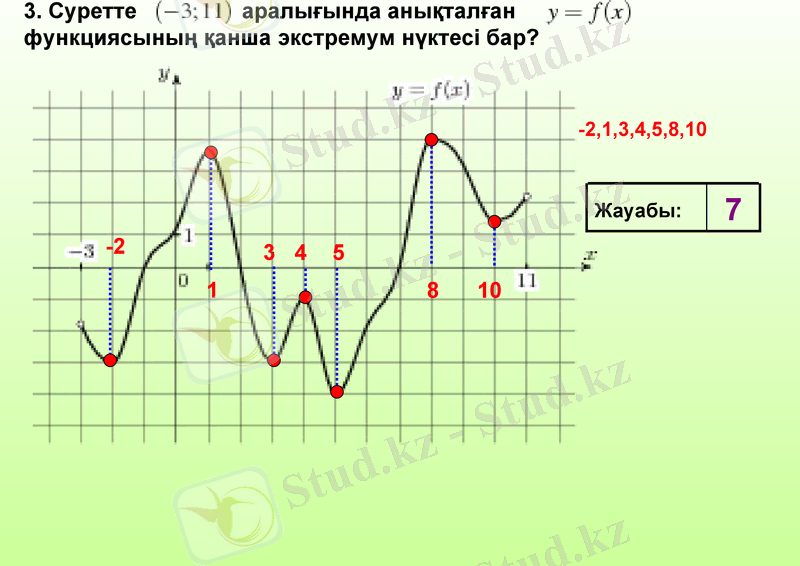
Жауабы:
7
3. Суретте аралығында анықталған функциясының қанша экстремум нүктеcі бар?
3
-2, 1, 3, 4, 5, 8, 10
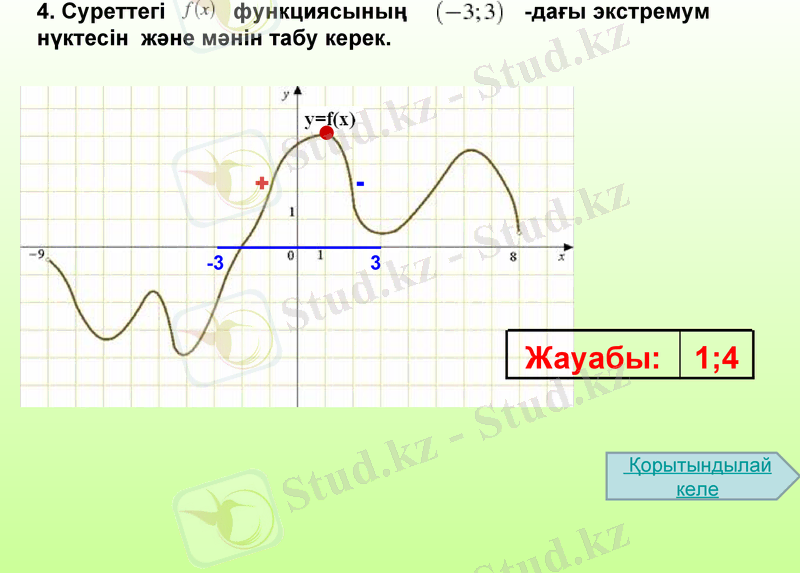
4. Суреттегі функциясының -дағы экстремум нүктесін және мәнін табу керек.
-3
3
Жауабы:
1; 4
+
-
Қорытындылай келе
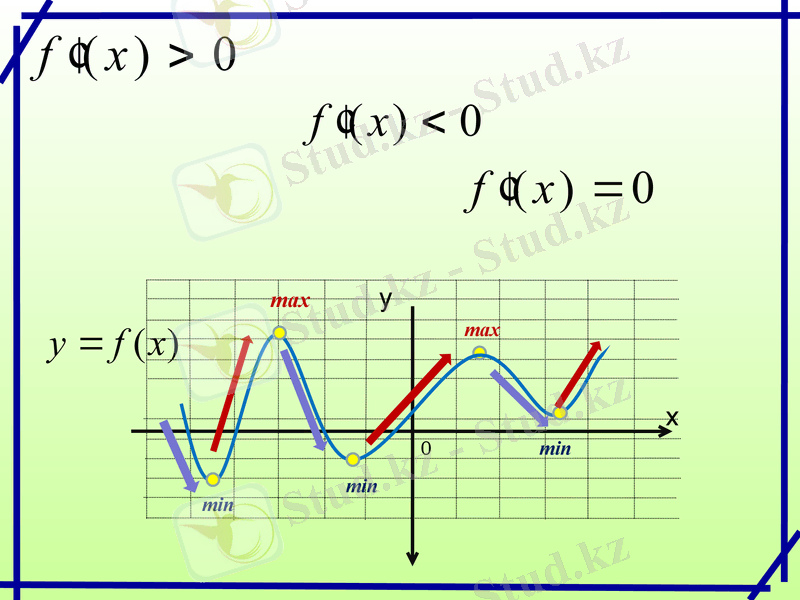
0
min
max
min
min
max
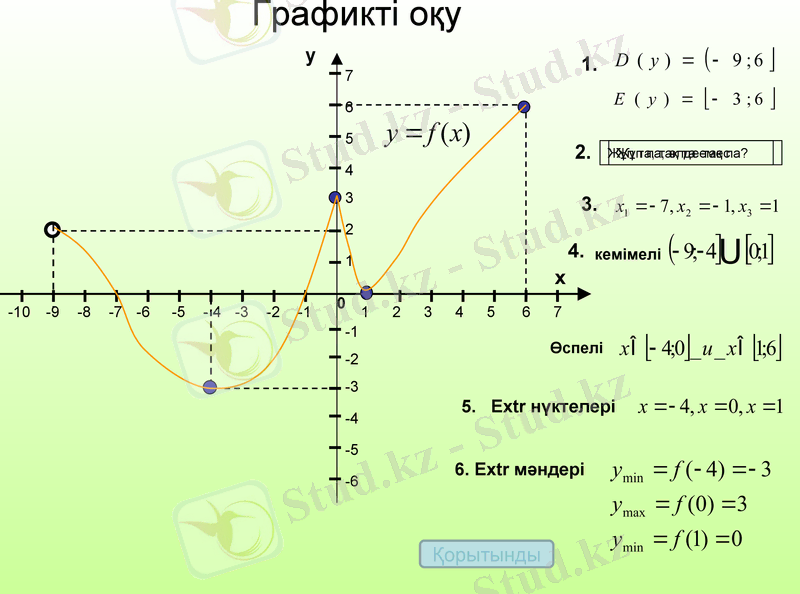
Графикті оқу
0
1
5
2
3
4
7
6
х
у
1
3
2
4
5
6
7
-2
-1
-1
-2
-3
-6
-5
-5
-4
-3
- 4
-8
-7
-6
-10
-9
Жұп па, әлде тақ па?
кемімелі
Өспелі
1.
2.
4.
3.
6. Extr мәндері
5. Extr нүктелері
Жұп та, тақ та емес
Қорытынды

Жаңа сабақ

Туындының көмегімен функцияны зерттеу және оның графигін салу

Анықталу обл. (D) табу.
Жұп-тақтыққа зерттеу: y(-x) =y(x) жұп (графигі Оу өсіне қар/да симм. )
y(-x) = -y(x) тақ (графигі О-коор. бас нүкт. қар/да симм. )
Периодтылыққа зерттеу.
Ох, Оу өстерімен қиыл. нүкт/н табу: y=0 (Ох өсімен қиыл. нүкт. ),
x= 0 (Оу өсімен қиыл. нүкт. )
Таңба тұрақтылық аралықтарын табу:
y>0 (графиктің Ох өсінен жоғ. жатқан бөлігі),
y<0 (графиктің Ох өсінен төм. жатқан бөлігі),
Өсу, кему аралықтарын, extr табу.
Асимптоталарын табу:
а) верт. асимпт. : х=a -түзуі, егер
б) көлбеу асимпт. -түзуі, егер
Кесте құру.
Функцияны зерттеп, графигін салу алгоритмі:
x
y

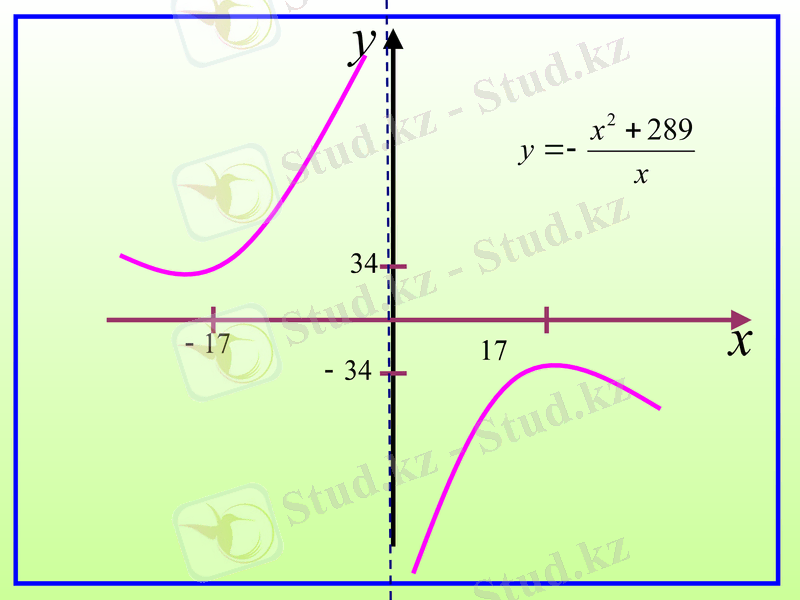
Функцияны зерттеп, графигін тұрғыз.
min max
2. Функция -тақ, ендеше графигі О-коор. басына қар/да симм.
4. Функцияның асимптотасын табамыз.

б) Көлбеу асимптота: y=kх+b түзуі, мұндағы k, b сандары келесі формулалардан табылады:
4. Функцияның асимптоталарын табамыз.
а) Вертикаль асимптота: х=0 түзуі (Оу өсі), себебі:
∞, ендеше көлбеу асимптотасы жоқ.
5. Зерттеулер негізінде кесте құрамыз:
x
(-∞; -17)
-17
(-17; 0)
0
(0; 17)
17
(0; +∞)
f / (x)
-
0
+
-
+
0
-
f (x)
34
-
-34
extr
min
-
max
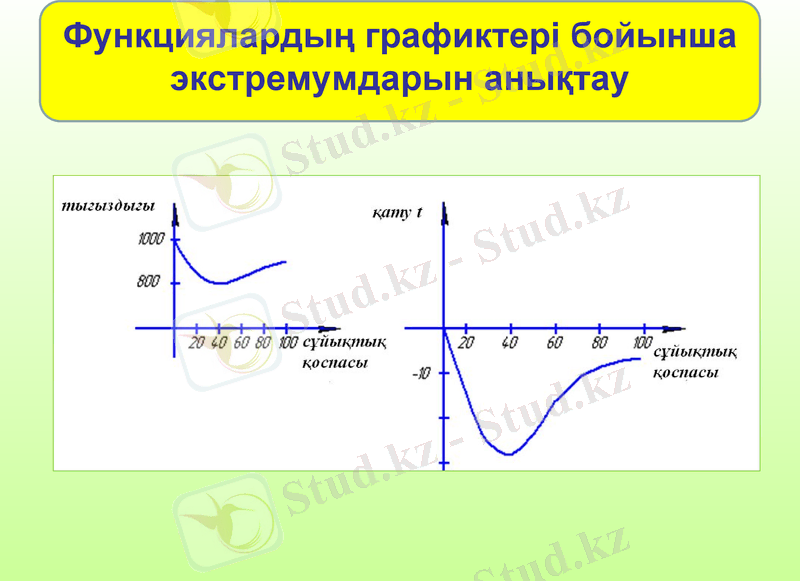
Функциялардың графиктері бойынша экстремумдарын анықтау
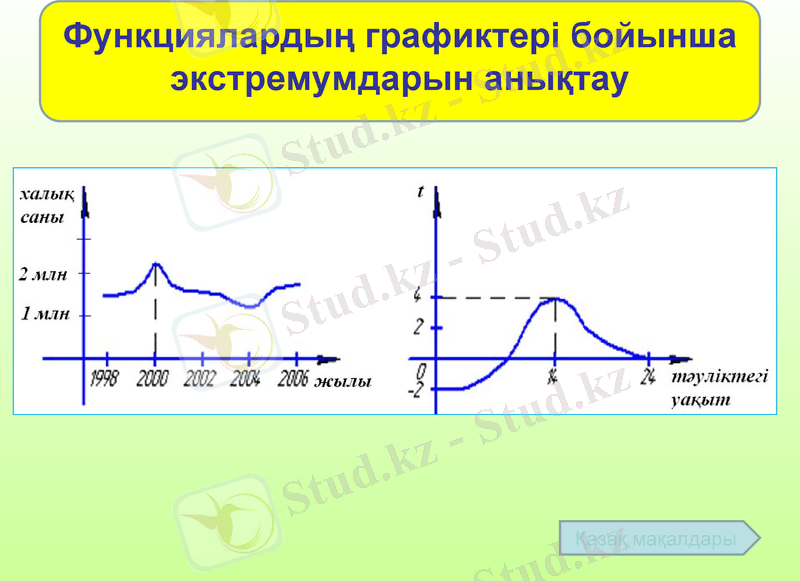
Функциялардың графиктері бойынша экстремумдарын анықтау
Қазақ мақалдары
Көп сөйлеген білімді емес, дөп сөйлеген білімді.
t cөйлеу
max нүктесі
f(a) -функция максимумы
білім
Білімнің басы - бейнет, соңы - зейнет.
білім
max нүктесі
f(a) -функция максимумы
бейнет
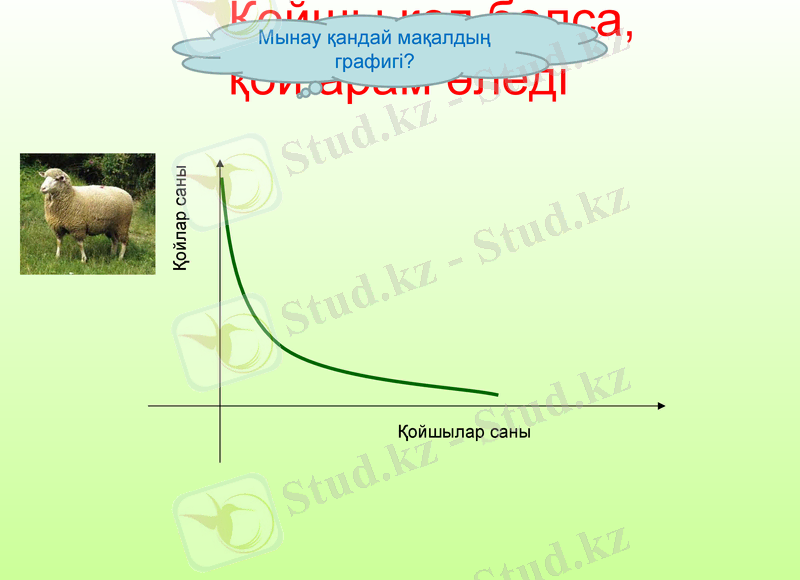
Қойшы көп болса, қой арам өледі
Қойшылар саны
Қойлар саны
Мынау қандай мақалдың графигі?
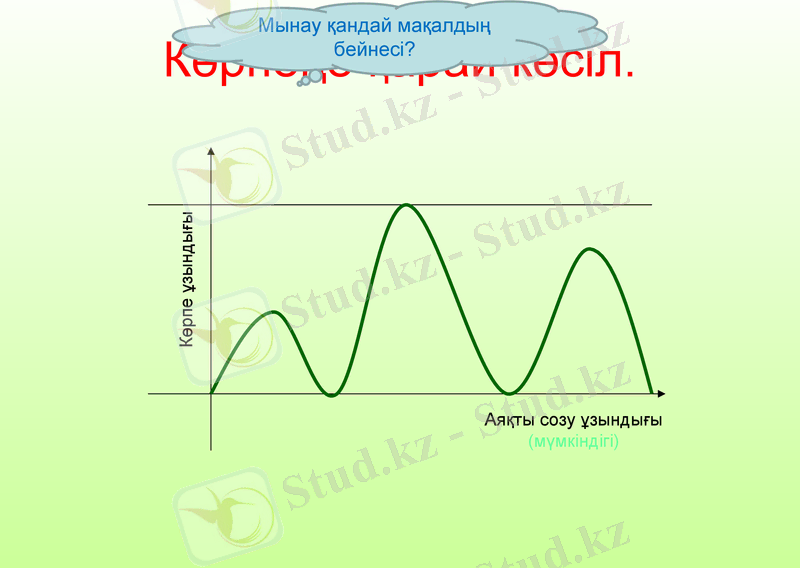
Көрпеңе қарай көсіл.
Аяқты созу ұзындығы
(мүмкіндігі)
Көрпе ұзындығы
Мынау қандай мақалдың бейнесі?
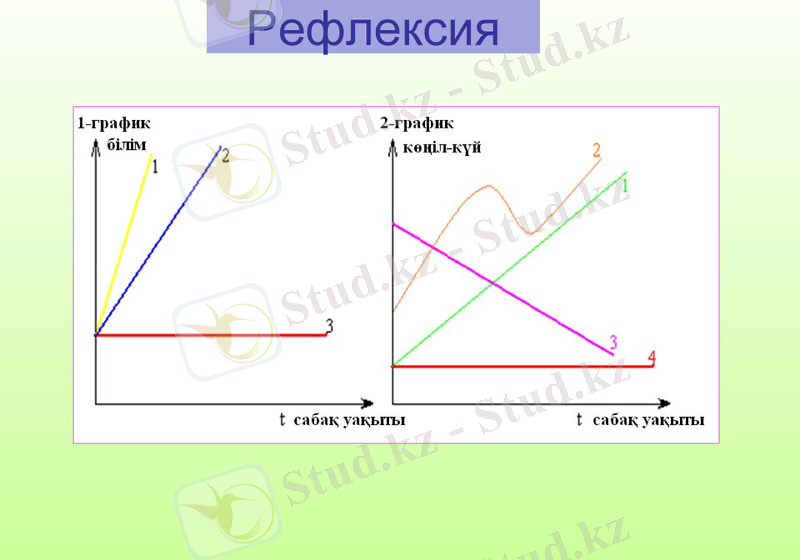
Рефлексия

Сабақтың қорытындысы:
«Бүгінгі сабақ … ұнады»
«Бүгінгі сабақта …білдім»
«Бүгінгі сабақта … үйрендім»
«Бүгінгі сабақта … таныстым»
«Бүгінгі сабақта … қайталадым»
«Бүгінгі сабақта … түсіндім»
«Бүгінгі сабақ … таңқалдырды»
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz