Cos х = а, Sin х = а, tg х = а, ctg x = a түріндегі қарапайым тригонометриялық теңдеулер

Скачать

Сабақтың тақырыбы:

«Cos х = а, Sin х = а, tg х = а, ctg x = a түріндегі қарапайым тригонометриялық теңдеулер. »

Сабақтың мақсаты:

Білімділік: Қарапайым тригонометриялық теңдеулер туралы түсінік беру, қарапайым тригонометриялық теңдеулерді шешу тәсілдерін үйрету.

Дамытушылық : Білім алушыларды өз бетімен іс-әрекет ете білу дағдысын, логикалық ойлау қабілетін, шығармашылық ізденістерін қалыптастыру.

Тәрбиелік мақсаты: Пәнге деген қызығушылығын арттыру, жүйелі түрде жұмыс істеуге, өз ойын дәл, тиянақты айта білуге, заман талабына сай, бәсекеге қабілетті жеке тұлға тәрбиелеу.

Сабақтың типі: Жаңа тақырыпты меңгерту.

Сабақтың әдісі:Аралас сабақ

Сабақтың көрнекілігі:интерактивті тақта, слайдтар, тест тапсырмасы

Сабақтың жоспары :

І. Ұйымдастыру

ІІ. Үй тапсырмасын тексеру, өткен сабақты пысықтау.

а) Қайталау сұрақтары. (Графикалық диктант)

ә) Математикалық диктант «Есептеңдер!»

б) Қатесін тап

ІІІ. Жаңа білімді меңгерту.

ІV. Оқулықпен жұмыс

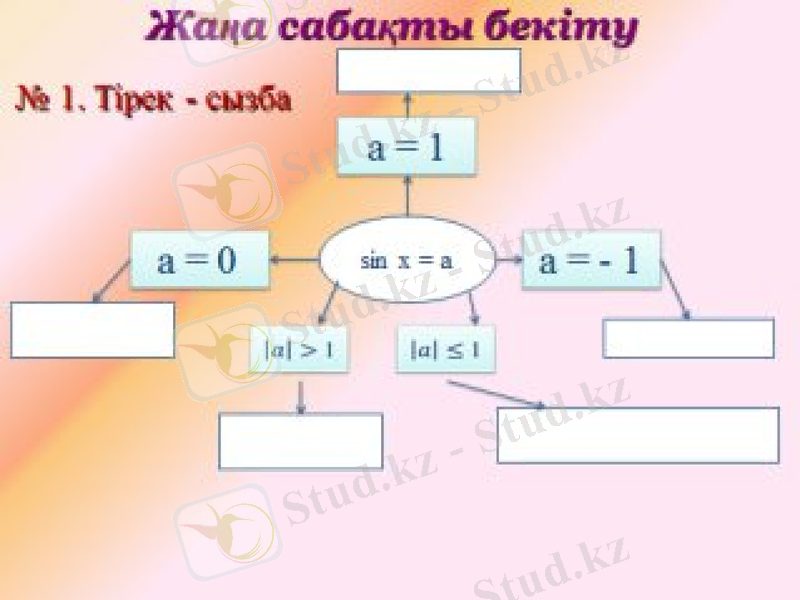
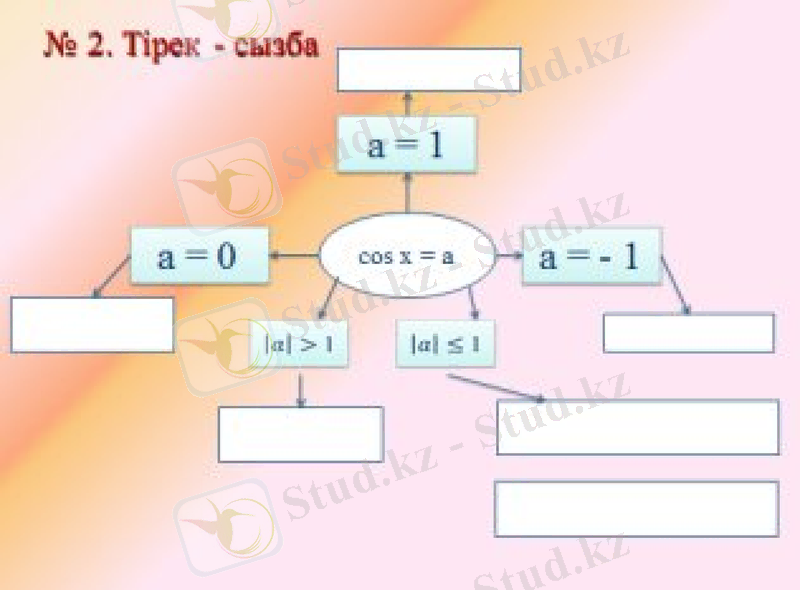
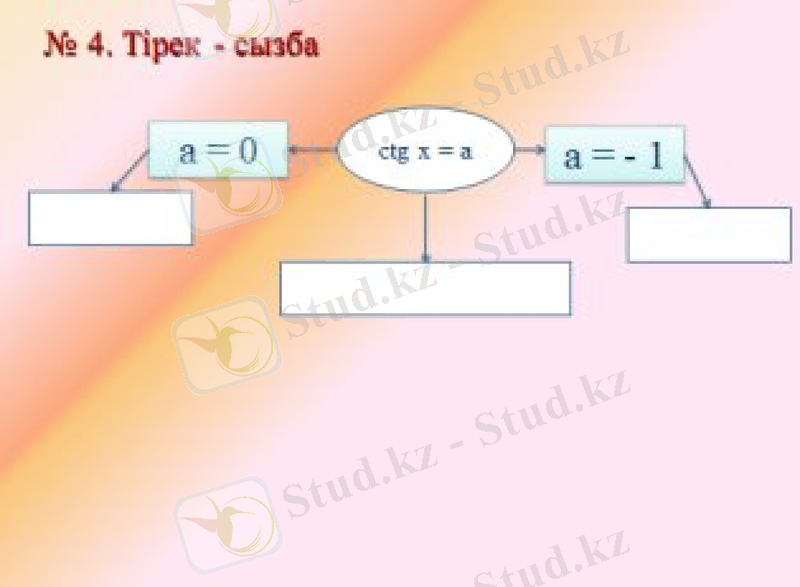
V. Жаңа сабақты бекіту (Тірек- сызба)

VІ. Сәйкесін тап

VІІ. Қорытындылау.

Үйге тапсырма

Қайталау сұрақтары . (Графикалық диктант)

1. Тригонометриялық функциялар түрлері?

2. Тригонометриялық функцияның негізгі

қасиеттері қандай?

3. Тригонометриялық функцияның

графиктері қалай аталады?

4. Арксинус дегеніміз не?

5. Арккосинус қалай анықталады?

6. Арктангенс дегеніміз не?

7. Арккотангенс дегеніміз не?

Математикалық диктант «Есептеңдер!»

1) arctg(-1) - arctg1

2) tg (arctg( ) )

)

3) arcsin1-arccos( - )

4) cos(arcсos (- ) )

Анықтама: sin x=a, cos x=a,

tg x=a, ctg x=a түрінде

берілген теңдеулерді

қарапайым тригонометриялық

теңдеулер деп атайды.

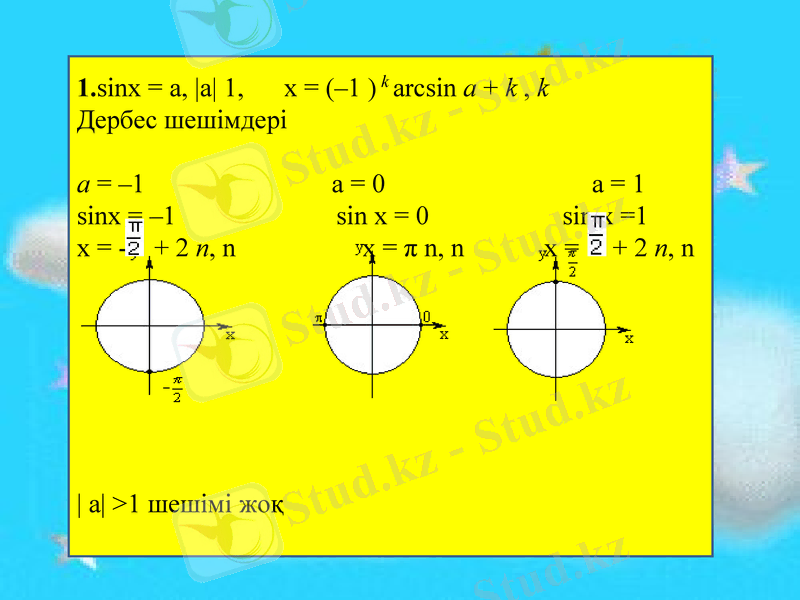
1. sinx = a, a 1, x = (-1 ) k arcsin a + k, k

Дербес шешімдері

a = -1 a = 0 a = 1

sinx = -1 sin x = 0 sin x =1

x = - + 2 n, n x = π n, n x = + 2 n, n

a >1 шешімі жоқ

2. cosx = a, a 1

x = ± arccosa+ 2 n, n дербес түрлері

a= -1 a= 0 a = 1

cosx = -1 cosx = 0 cosx = 1

x = π + 2 n, n x = + n, n x = 2π n, n

a >1 шешімі жоқ.

Қарапайым тригонометриялық теңдеулер

шешімдерінің жалпы түрі

Шешімдердің дербес түрлері

Мысалдар қарастыру:

Мысал қарастыру:

1-мысал: теңдеуін шешейік

2-мысал: теңдеуін шешейік:

3-мысал

tg теңдеуін шешейік:

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс