8-сынып алгебрасы: квадрат теңдеулер - анықтама, түрлері және шешу әдістері

Скачать

КВАДРАТ

теңдеулер

Алгебра 8 сынып

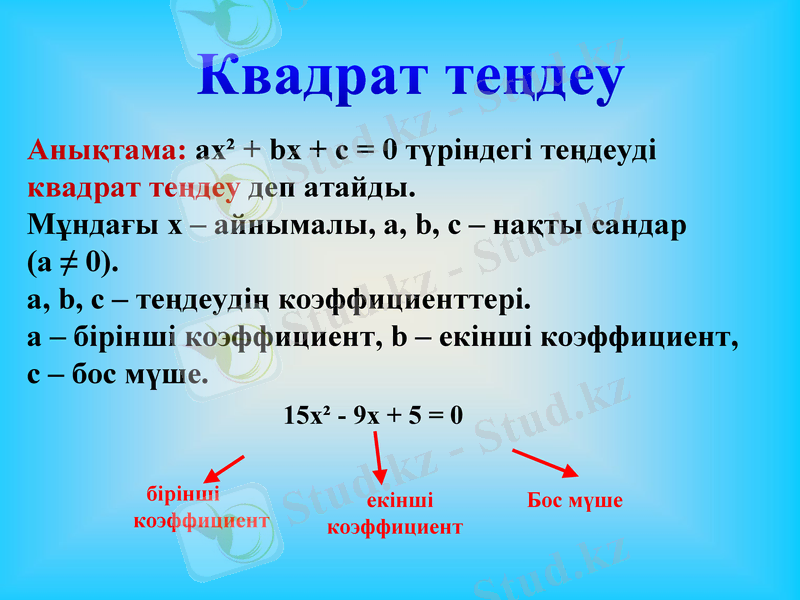
Анықтама: ах² + bх + с = 0 түріндегі теңдеуді квадрат теңдеу деп атайды.

Мұндағы х - айнымалы, а, b, с - нақты сандар

(а ≠ 0) .

а, b, с - теңдеудің коэффициенттері.

а - бірінші коэффициент, b - екінші коэффициент,

с - бос мүше.

15х² - 9х + 5 = 0

бірінші коэффициент

екінші коэффициент

Бос мүше

Квадрат теңдеу

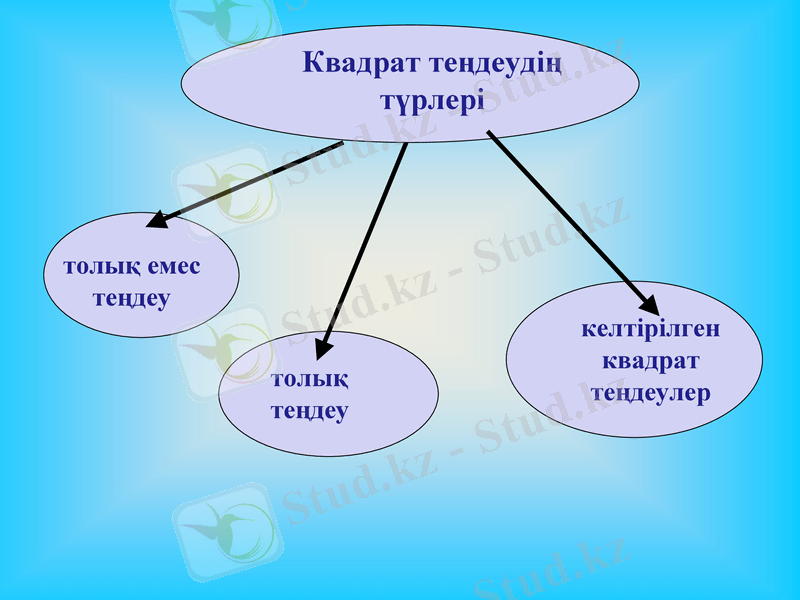
Квадрат теңдеудің түрлері

толық емес теңдеу

толық теңдеу

келтірілген квадрат теңдеулер

Толық квадрат теңдеу

Егер толық квадрат теңдеудегі бірінші коэффициент 1-ге тең (a=1) болса, онда ол келтірілген квадрат теңдеу деп аталады.

Келтірілген квадрат теңдеу

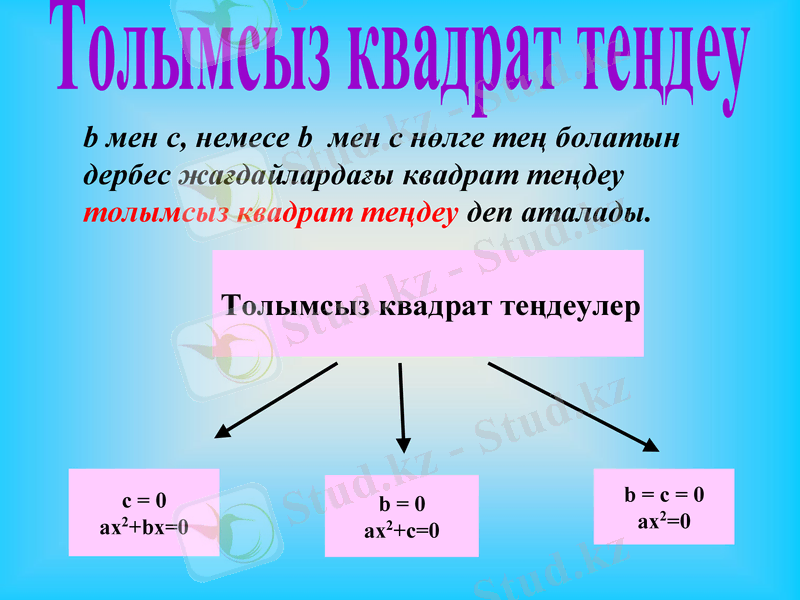
Толымсыз квадрат теңдеу

b мен с, немесе b мен с нөлге тең болатын дербес жағдайлардағы квадрат теңдеу толымсыз квадрат теңдеу деп аталады.

Толымсыз квадрат теңдеулер

с = 0

ax2+bx=0

b = 0

ax2+c=0

b = c = 0

ax2=0

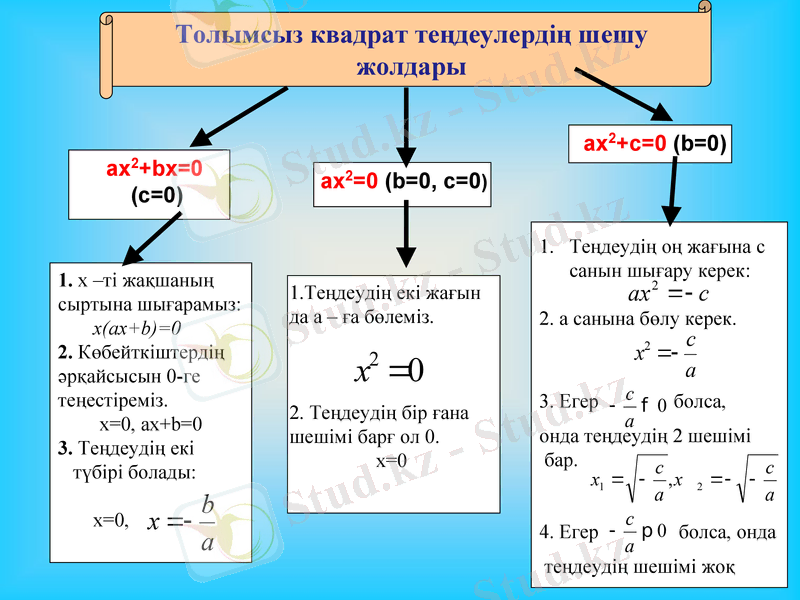
Толымсыз квадрат теңдеулердің шешу жолдары

Берілген теңдеулерден квадрат теңдеулерді теріп жазып алыңыздар.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс