11-сынып: Интеграл арқылы фигуралардың ауданы мен айналу денелерінің көлемін есептеу

Алгебра және анализ бастамалары

Геометриялық және физикалық

есептерде интегралды қолдану

11 сынып

Тоқмұхамедов Қ. Қ. атындағы жалпы білім беретін №14 орта мектептің

математика пәнінің мұғалімі Сарсенбаева Ляззат

а) білімділік: оқушылардың алғашқы функция

және интеграл туралы білімдерін жүйелеу және

бекіту, оқушыларды интегралдың көмегімен

фигуралардың ауданы мен көлемін таба білуге

үйрету

ә) дамытушылық: оқушылардың логикалық

ойлау қабілетін дамыту, танымдық

қызығушылығын арттыру

б) тәрбиелік: компьютерлік технология арқылы

оқушы біліктілігін арттыру, оқушыларды

бір-бірімен достық қарым-қатынасқа, ұжымдық

жұмыс жасауға тәрбиелеу, шығармашылық

қабілетін жетілдіру

Сабақтың мақсаты:

Сабақтың типі: жалпылау және қорытындылау

сабағы

Сабақтың түрі: дәстүрлі сабақ

Сабақтың әдісі: сұрақ-жауап, түсіндіру, өз бетімен жұмыс жасау, сәйкестендіру тестісі, топтық жұмыс, деңгейлеп оқыту

Пән аралық байланыс: геометрия, сызу

Сабақтың көрнекілігі: интерактивті тақта, компьютер, слайдтар, деңгейлік тапсырмалар,

сызғыш, түрлі-түсті бор, кесте.

“Ой қозғау”

№

Функция

Алғашқы функцияның жалпы түрі

f(х) = к(к - тұрақты)

F (х) = k x + C

f(х) = ха, а Z, а ≠ -1

F (х) = + C

f(х) =

F (х) = 2 + C

f(х) = sin x

F (х) = -

f(х) = cos x

F (х) =

f(х) =

F (х) = tg x + C

f(х) =

F (х) = - ctg x + C

“Орнын тап” сәйкестендіру тестісі

№

Сұрақ

№

Жауап

Анықталмаған интегралды табу формуласы

1-2

Ньютон - Лейбниц формуласы

2-3

F (х) + C

Қисық сызықты трапецияның ауданын есептеу формуласы

3-4

Айналу денесінің көлемін табу формуласы

4-1

S =

1-топ. № 50-есеп

f (х) = - х2 + 4х - 4 функциясының графигімен және координата осьтерімен шектелген фигураның ауданын табыңдар

Шешуі: f (х) = - х2 + 4х - 4 функциясының графигі - тармағы төмен қараған парабола болады. Параболаның бас нүктесінің координаттары (2; 0)

1- деңгейдегі тапсырма

Ньютон - Лейбниц формуласы бойынша

S =

(

кв. бірлік

Жауабы:

кв. бірлік

у=-х2+4х - 4

-4

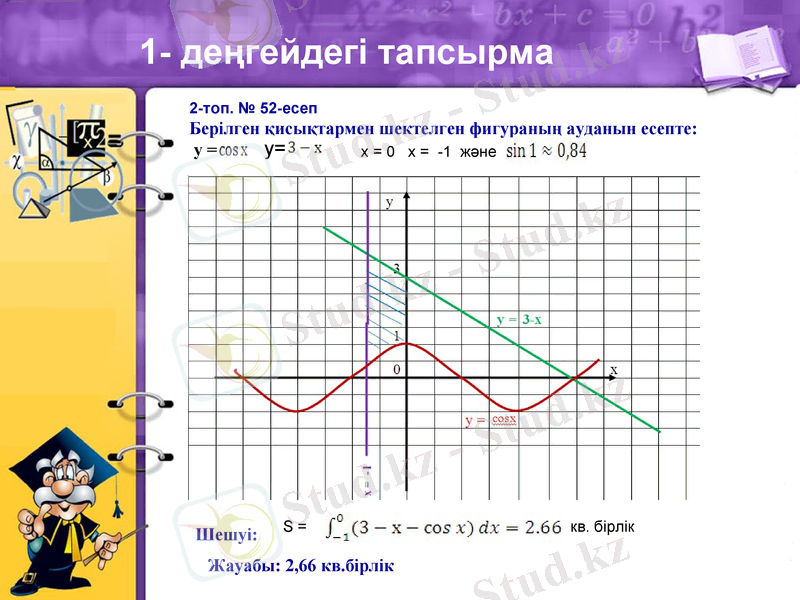
2-топ. № 52-есеп

Берілген қисықтармен шектелген фигураның ауданын есепте:

у =

1- деңгейдегі тапсырма

х = 0 х = -1 және

у=

Шешуі:

S =

кв. бірлік

Жауабы: 2, 66 кв. бірлік

Шешуі: Графиктердің қиылысу нүктелерінің координаттарын табамыз

3 х2= 2 х Бұдан х1= 0 х2 =

2- деңгейдегі тапсырма

1-топ. №55-есеп

у = 3 х2 және у = 2х функциялардың графиктерімен шектелген фигураның ауданын тап.

кв. бірлік

Сонда S=

кв. бірлік

Жауабы:

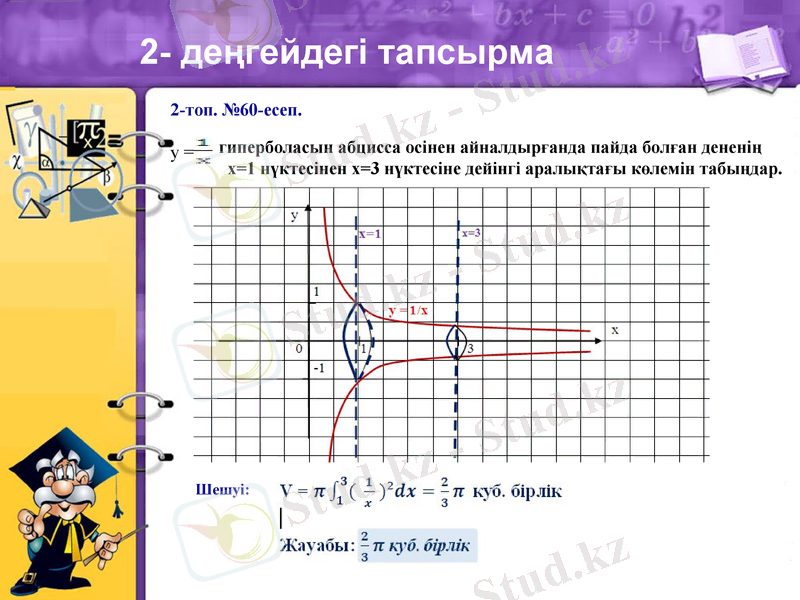
2- деңгейдегі тапсырма

2-топ. №60-есеп.

у =

гиперболасын абцисса осінен айналдырғанда пайда болған дененің

х=1 нүктесінен х=3 нүктесіне дейінгі аралықтағы көлемін табыңдар.

Шешуі:

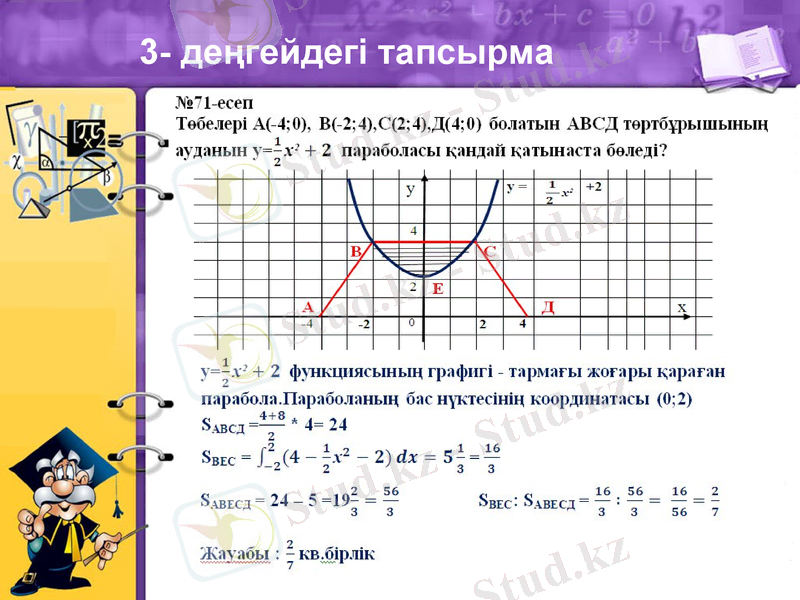
3- деңгейдегі тапсырма

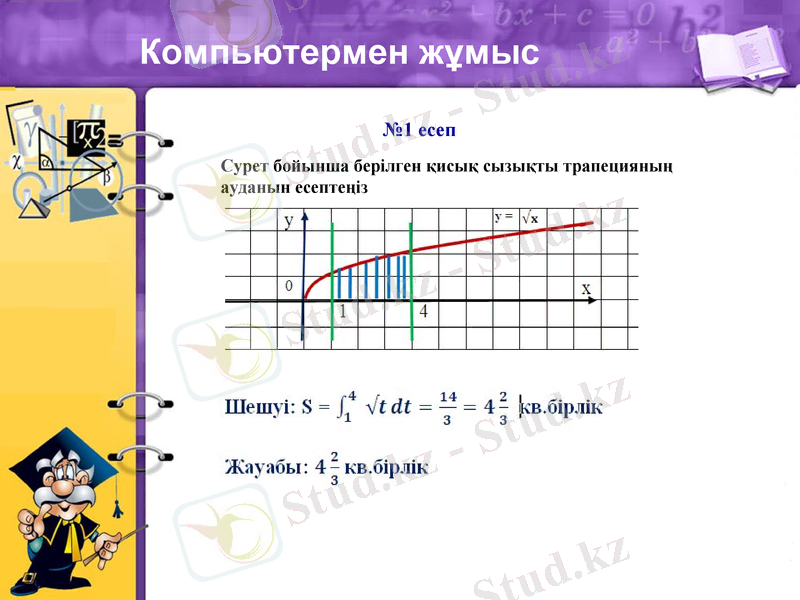
Компьютермен жұмыс

№1 есеп

Сурет бойынша берілген қисық сызықты трапецияның ауданын есептеңіз

Компьютермен жұмыс

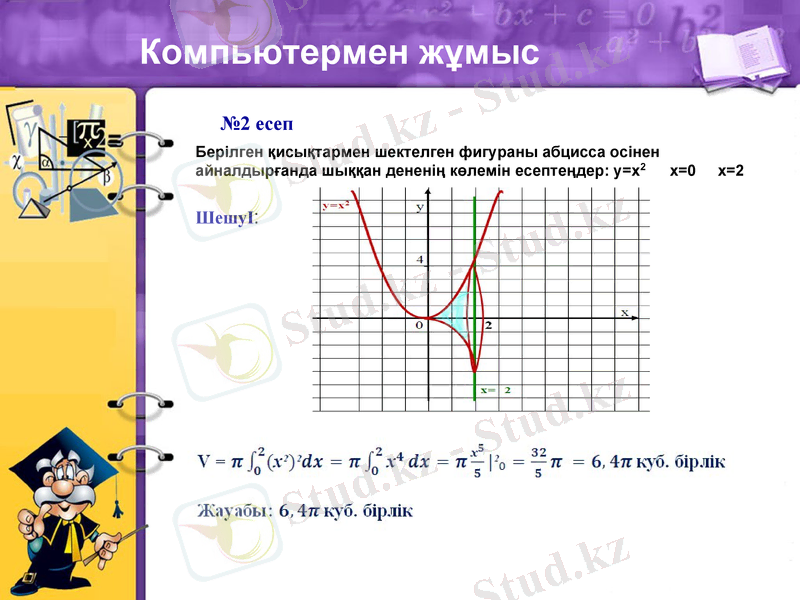
№2 есеп

Берілген қисықтармен шектелген фигураны абцисса осінен айналдырғанда шыққан дененің көлемін есептеңдер: у=х2 х=0 х=2

ШешуІ:

Тест

Үйге тапсырма

1-тарау

№54 және №57 есептер

Ақпараттық технология сабақта

Есеп шығару кезеңдері

Ұқсас жұмыстар

Алғашқы функция және интеграл: 11-сынып математика сабағының жоспары мен жаттығулары

Анықталған интеграл: есептеу әдістері мен қолданылуы

Үш еселі интеграл: теориясы, есептеу әдістері және қолданбалары

Анықталмаған интеграл: анықтамасы, қасиеттері және есептеу әдістері

Анықталған интеграл: анықтама, негізгі теоремалар, есептеу әдістері және қолданылуы

Жазық фигуралардың аудандары: ұғымы, қасиеттері және есептеу формулалары

Конус: анықтама, элементтері және бет аудандары мен көлемін есептеу

Спектрлік талдау арқылы аспан денелерінің химиялық құрамы мен тығыздығын анықтау

Жазық фигуралардың ауданын есептеуде анықталған интегралды қолдану: әдістер мен сабақ үлгілері

8-сынып химиясы: химиялық теңдеулер бойынша зат мөлшері, масса және газ көлемін есептеу

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz