Математика (10-сынып): көрсеткіштік және логарифмдік функциялардың графиктері мен қасиеттері

Көрсеткіштік функцияның графигі мен қасиеттері

Математика 10 сынып

Шымкент қаласы химия-биология бағытындағы Назарбаев Зияткерлік мектебі

Шокибаева А. Н.

МН10. 15 y = ax (a> 0, a ≠ 1) көрсеткіштік функцияға кері

функция y = loga(x) логарифмдік функция екенін түсінеді

МН10. 16 көрсеткіштік және логарифмдік функциялардың

қасиеттерін қорытып шығарады;

МН10. 17 көрсеткіштік және логарифмдік функциялардың

өзара кері тәуелділігін пайдалана отырып, олардың

қасиеттерін салыстырады;

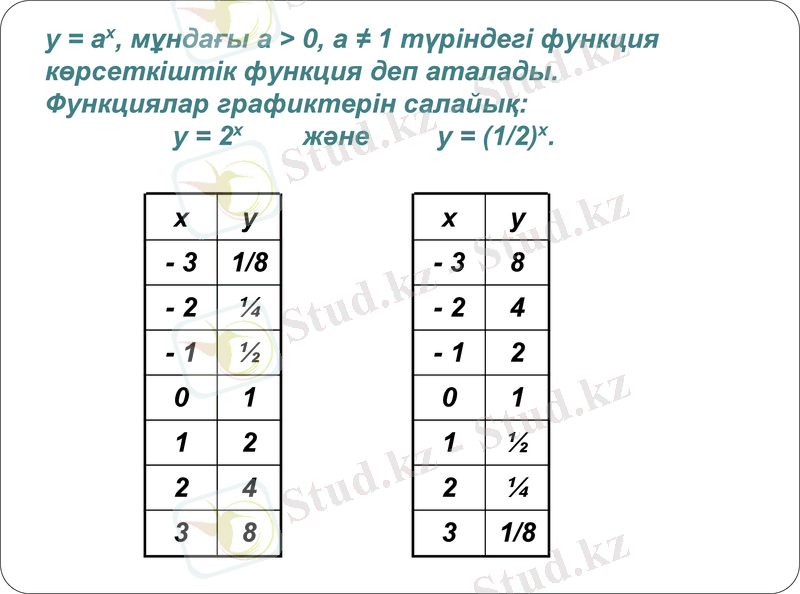
у = ах, мұндағы а > 0, а ≠ 1 түріндегі функция көрсеткіштік функция деп аталады.

Функциялар графиктерін салайық:

у = 2х және у = (1/2) х.

- 3

1/8

- 2

- 1

- 3

- 2

- 1

1/8

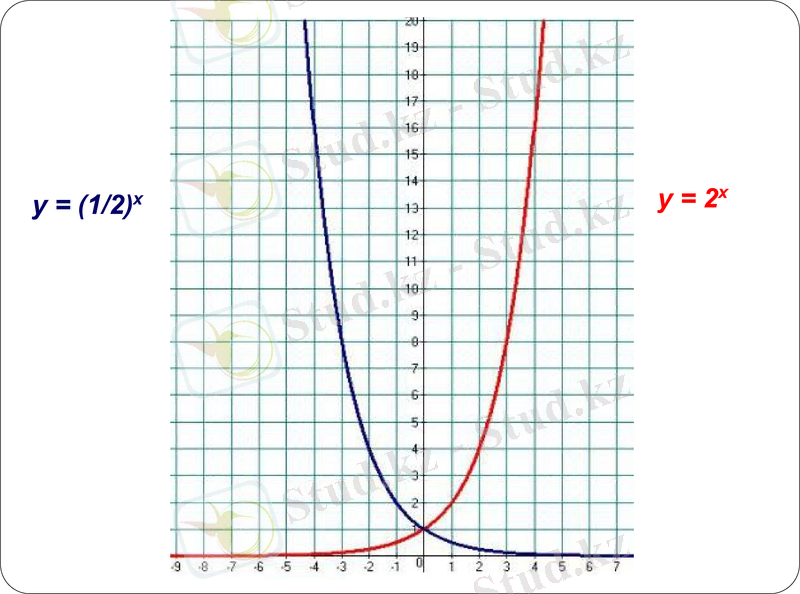
у = (1/2) х

у = 2х

у = ах, мұндағы 0< а < 1 функциясының қасиеті

D(f) = (- ∞; + ∞) ;

Тақ та емес, жұп та емес;

Кемімелі;

Төменнен шектелген;

Ең үлкен және ең кіші мәні жоқ;

Үзліссіз ;

E(f) = (0; +∞), ax > 0;

Ассимптотасы - Ох өсі

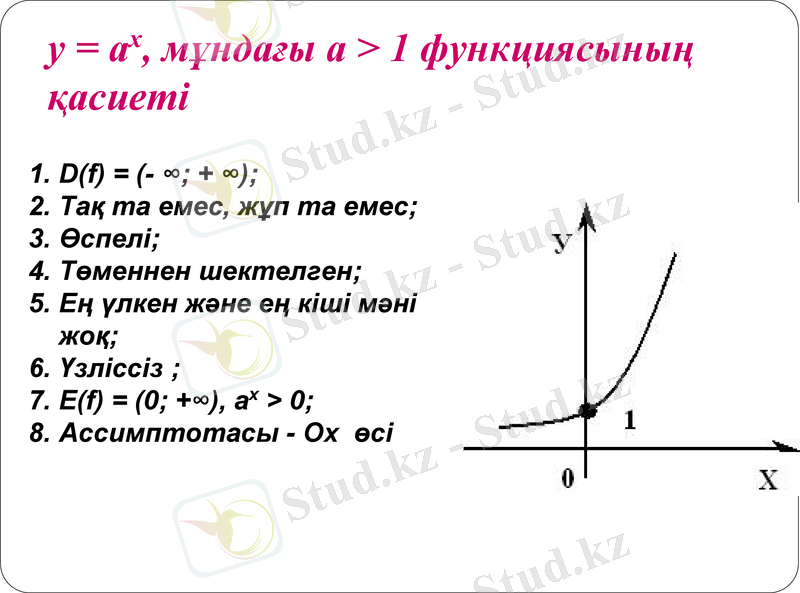
у = ах, мұндағы а > 1 функциясының қасиеті

D(f) = (- ∞; + ∞) ;

Тақ та емес, жұп та емес;

Өспелі;

Төменнен шектелген;

Ең үлкен және ең кіші мәні жоқ;

Үзліссіз ;

E(f) = (0; +∞), ax > 0;

Ассимптотасы - Ох өсі

Логарифмдік функцияның графигі мен қасиеттері

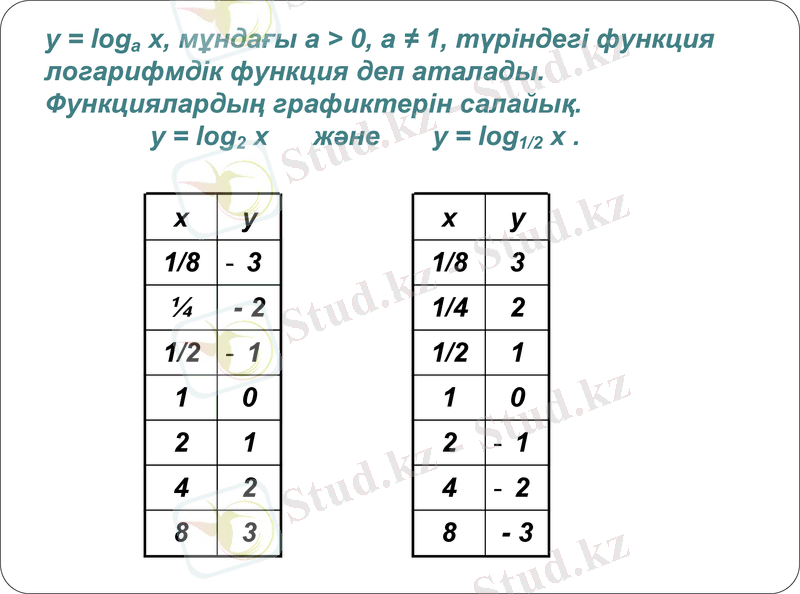
у = loga x, мұндағы а > 0, а ≠ 1, түріндегі функция логарифмдік функция деп аталады.

Функциялардың графиктерін салайық.

у = log2 x және у = log1/2 x .

1/8

- 2

1/2

1/8

1/4

1/2

- 3

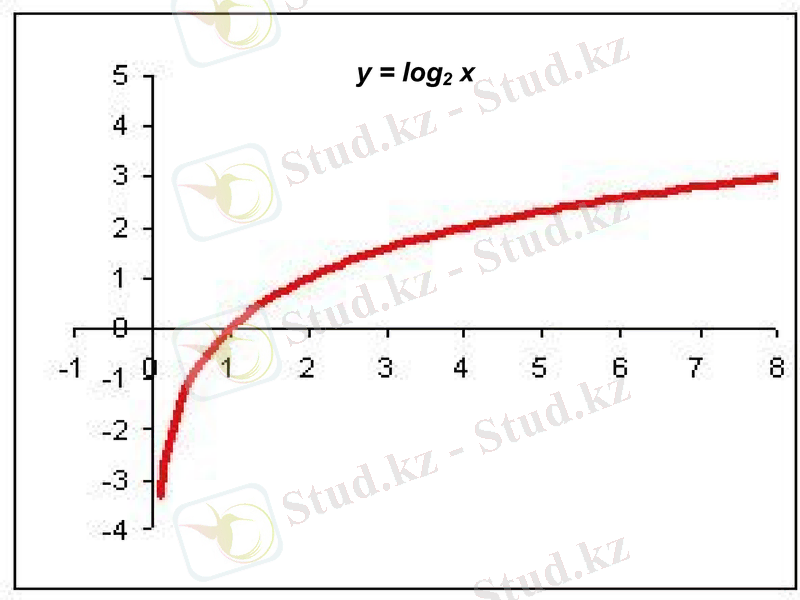
y = log2 x

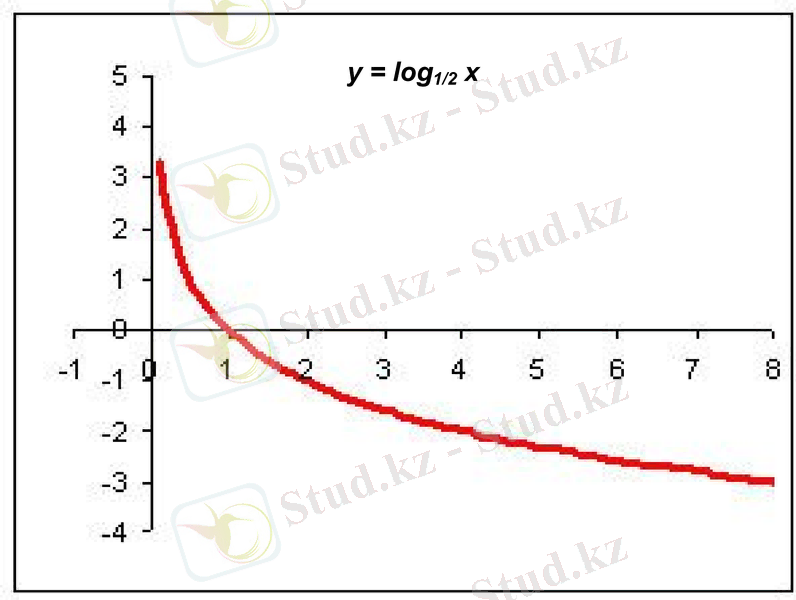
y = log1/2 x

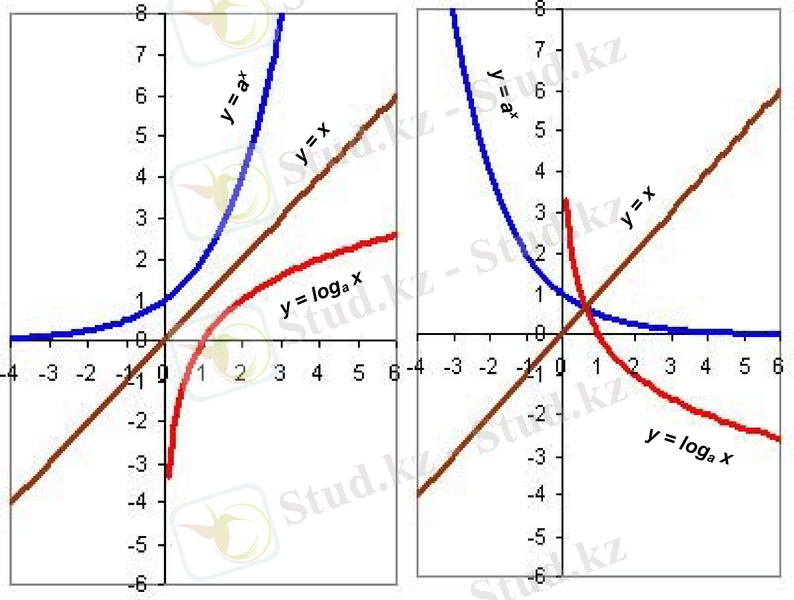
y = loga x

y = ax

y = x

у = loga x, мұндағы а > 1 функциясының қасиеттері

D(f) = (0; + ∞) ;

Тақ та емес, жұп та емес;

Өспелі;

Жоғарыдан да төменнен де шектелмеген;

Ең үлкен және ең кіші мәні жоқ;

Үзіліссіз;

E(f) = (- ∞; +∞) ;

Ассимптотасы - Оу өсі

у = loga x, мұндағы 0 < а < 1 функциясының қассиетері

D(f) = (0; + ∞) ;

Тақ та емес, жұп та емес;

Кемімелі;

Жоғарыдан да төменнен де шектелмеген;

Ең үлкен және ең кіші мәні жоқ;

Үзіліссіз;

E(f) = (- ∞; +∞) ;

Ассимптотасы - Оу өсі

Ұқсас жұмыстар

Көрсеткіштік және логарифмдік өрнектерді түрлендіру: анықтамалар мен қасиеттері

Көрсеткіштік және логарифмдік функциялар: қасиеттері, теңдеулер мен теңсіздіктерді шешу әдістері

Айнымалы негізді көрсеткіштік және логарифмдік теңсіздіктерді шешудің әдістері мен алгоритмі

Негізі айнымалы көрсеткіштік және логарифмдік теңсіздіктерді шешудің тиімді әдістері

Ондық және натурал логарифмдер: көрсеткіштік және логарифмдік өрнектерді түрлендіру және мәнін есептеу

11-сынып алгебра: логарифмдік теңдеулерді шешу

sin x және cos x функцияларының қасиеттері, түрлендірулері мен графиктері

11-сынып математикасы: логарифмдік теңдеулер мен теңсіздіктерге арналған сабақ жоспары

11-сынып алгебра: логарифмдік теңдеулерді қайталау және шешу әдістері

Логарифмдік теңдеулер және оларды шешу тәсілдері (11-сынып алгебрасы)

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz