Дұрыс көпжақтардың симметриясы

Презентация қосу

Дұрыс
көпжақтардың
симметриясы
• Дұрыс көпжақ ұғымы Евклидтің ХІІІ
кітабында жазылған. Евклид осындай
• көпжақтың бар екенін тағайындап,
оларға іштей сфераны қалай сызуға
болатынын көрсетеді.
1 Тетраэдр (грек сөзі «тетра» - төрт және
«едра» - жақ); 4 жақ, 4 төбе, 6 қыр;

2 Гексаэдр (куб) («гекса» - алты); 6 жақ, 8
төбе, 12 қыр;

3 Октаэдр («окто» - сегіз); 8 жақ, 6 төбе, 12
қыр;

4 Додекаэдр («додека» - он екі); 12 жақ, 20
төбе, 30 қыр;

5 Икосаэдр («эйкоси» - жиырма); 20 жақ,
12 төбе, 30 қыр.
• Евклид ХІІІ кітабында осы бес денеден басқа дұрыс
көпжақтың жоқ екенін дәлелдеген.
• Егер дөңес көпжактың барлық жақтары тең дүрыс
көпбұрыштар болса, сонымен қатар оның әрбір
төбесінде саны бірдей қырлар тоғысатын болса,
ондай дөңес көпжақ дұрыс көпжақ деп аталады.
Мысалы, куб дүрыс көпжак болып табылады. Оның
барлық жақтары тең квадраттар жөне әр төбесінде
үш қыр тоғысады.
Дұрыс тетраздр
Барлық қырлары тең дұрыс
тетраэдрден дұрыс
үшбұрышты пирамиданың
өзгешелігі оның бүйір қырлары
бір-біріне тен болғанмен, олар
табанының кабырғаларына
тең болмауы мүмкін.) төрт
теңқабырғалы үшбұрыштан
тұрады. Оның әрбір төбесі үш
үшбұрыштың төбесі болып
табылады. Демек, әрбір
төбедегі жазық бұрыштардың
қосындысы 180°-қа тең.
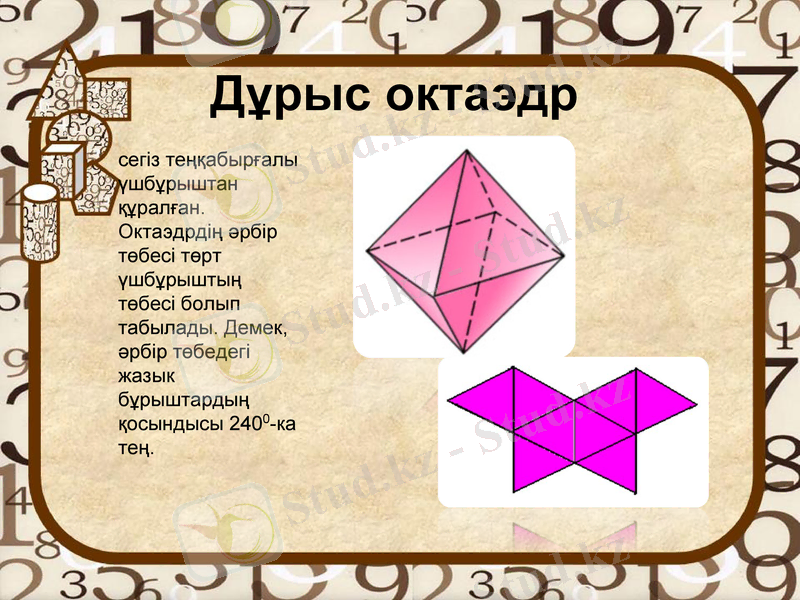
Дұрыс октаэдр
сегіз теңқабырғалы
үшбұрыштан
құралған.
Октаэдрдің әрбір
төбесі төрт
үшбұрыштың
төбесі болып
табылады. Демек,
әрбір төбедегі
жазык
бұрыштардың
қосындысы 2400-ка
тең.
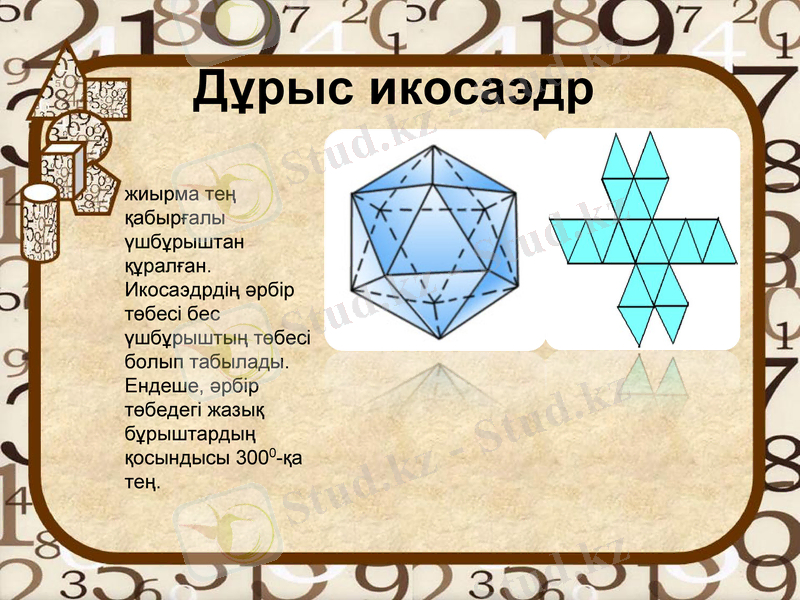
Дұрыс икосаэдр
жиырма тең
қабырғалы
үшбұрыштан
құралған.
Икосаэдрдің әрбір
төбесі бес
үшбұрыштың төбесі
болып табылады.
Ендеше, әрбір
төбедегі жазық
бұрыштардың
қосындысы 3000-қа
тең.
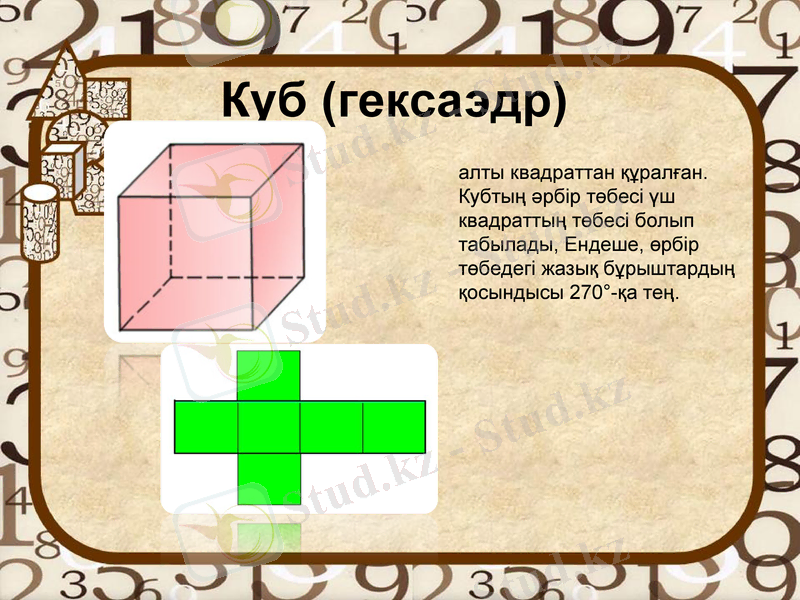
Куб (гексаэдр)
алты квадраттан құралған.
Кубтың әрбір төбесі үш
квадраттың төбесі болып
табылады, Ендеше, өрбір
төбедегі жазық бұрыштардың
қосындысы 270°-қа тең.
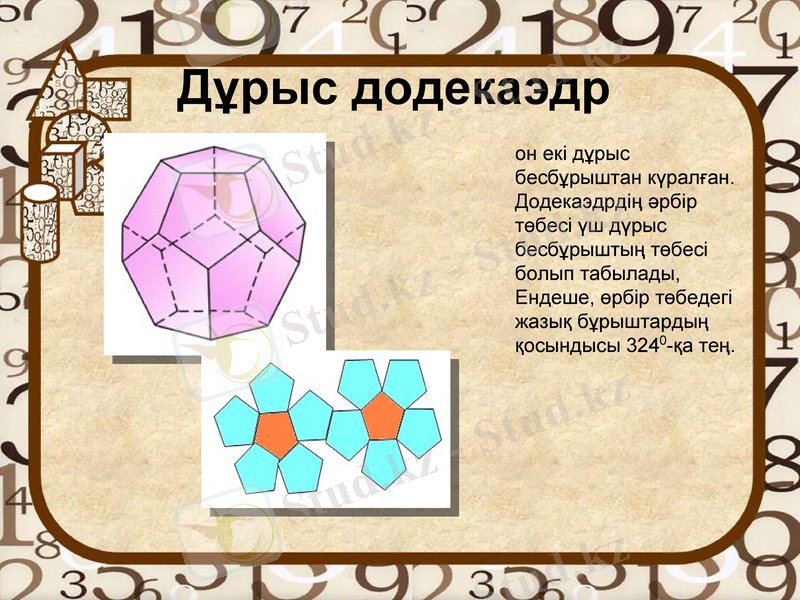
Дұрыс додекаэдр
он екі дұрыс
бесбұрыштан күралған.
Додекаэдрдің әрбір
төбесі үш дүрыс
бесбұрыштың төбесі
болып табылады,
Ендеше, өрбір төбедегі
жазық бұрыштардың
қосындысы 3240-қа тең.
•
• Дұрыс көпжақтардың осы аталып
өткен бес түрінен басқа түрлері жоқ.
•
• Дүрыс көпжактардың симметрия
элементтерін карастырайық.
Бет ауданы:

Тетраэдр көлемі :

Дұрыс тетраэдрдің симме
трия центрі жок. Қарама-
қарсы қырларының
орталары арқылы өтетін
түзу оның симметрия осі
болып табылады.
Куб диагональдарының қиылысу
нүктесі - оның жалғыз ғана
симметрия центрі болып
табылады. Қарама-қарсы жатқан
жақтардың центрлері және бір жақта
жатпайтын қарама-қарсы екі қырдың
орталары арқылы өтетін а жөне b
түзулері оның симметрия осьтері болып
табылады.
Бет ауданы:

Көлемі:
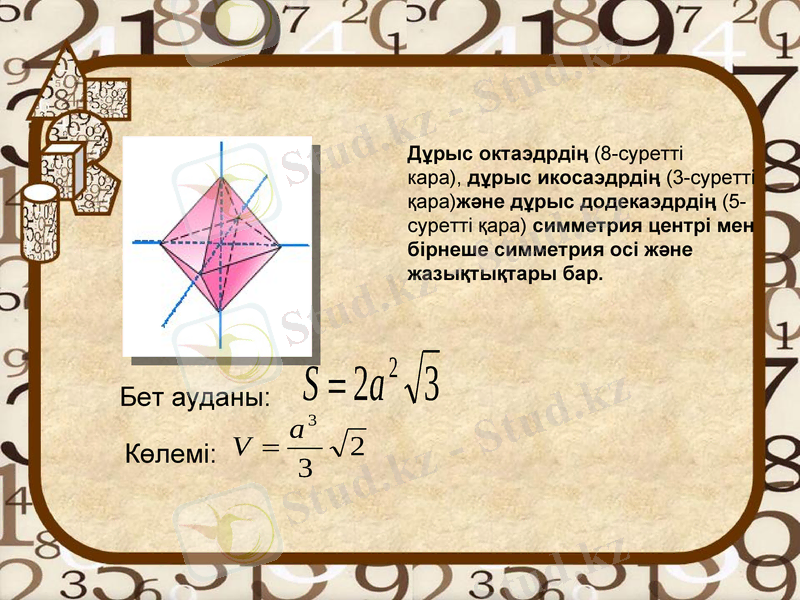
Дұрыс октаэдрдің (8-суретті
кара), дұрыс икосаэдрдің (3-суретті
қара)және дұрыс додекаэдрдің (5-
суретті қара) симметрия центрі мен
бірнеше симметрия осі және
жазықтықтары бар.

Бет ауданы:

Көлемі:
Дұрыс икосаэдрдің симметрия
элементтері:
Икосаэдрдің симметрия центрі -
икосаэдрдің центрі, 15 симметрия осі
және 15 симметрия жазықтығы бар.

Бет ауданы:

Көлемі:
Дұрыс додекаэдрдің симметрия
элементтері:
Додекаэдрдің симметрия центрі-
додекаэдрдің центрі, 15 симметрия осі
және 15 симметрия жазықтығы бар.

Бет ауданы:

Көлемі:

Ұқсас жұмыстар

Пирамиданың төбесін табанының нүктелерімен қосатын кесінділер - пирамиданың бүйір қырлары төбесі

КОСТЮМ КОМПОЗИЦИЯСЫ

Аморф заттар Кристалл заттар

Қөпжақтар Айналу денелері

Пирамиданың көлемін тап

Антигендік құрылымы

Альфавирустар тұқымдастығы

ҚҰТЫРУ ВИРУСЫ

Бирнавирутар туғызатын ауруларды диагностикалау

САЛУ ЕСЕПТЕРІН ШЕШУ ӘДІСТЕМЕСІ

Пәндер