Бөлшектің толқындық қасиеті

Презентация қосу

"Бөлшектің толқындық
қасиеті"
Бөлшек күйін кванттық
механикада бейнелеу.

Сәулелену кванттары – фотондардың екіжақты қасиеттері
болады, оларды бірінші жағдайда корпускулалар
(бөлшектер) ретінде, ал екінші жағдайда толқындар ретінде
қарастыруға болады. Осы идеяны 1923-1924 жылдары
нөлден өзгеше тыныштықтық массаға ие болатын
бөлшектерге арнап қолданған де Бройль болды. Оның
болжауынша, бұл бөлшектердің корпускулалық
қасиеттерімен қатар толқындық қасиеттері де болады.
Әрине, оның ғылыми болжамы сол кезде күтпеген өте батыл
ой болды.
Де Бройль қатысын басқа да қарапайым әдіспен алуға болады. Оптика курсынан белгілі, толқындық түйдектің
топтық жылдамдығы

формуламен сипатталады.
Осыдан де Бройль қатысын аламыз (интегралдау тұрақтысын нөлге теңестірсе)

Бұл өрнекті үйреншікті түрде жазуға болады

Осы қатыс де Бройль формуласы деген атпен белгілі.
Микробөлшектердің толқындық қасиеттері және
анықталмаушылық қатынасы.
Электрон әрі корпускулалық, әрі толқындық қасиеттері бар ерекше
бөлшек, оның кейде корпускулалық, кейде толқындық қасиеттері
білінеді; бұл сыртқы жағдайға байланысты. Әйтеуір электрон
классикалық бөлшек емес. Сондықтан электронды (сондай-ақ әрбір
элментар бөлшекті) макробөлшектерге тән физикалық шамалармен
тек жуықтап қана сипаттауға болады. Осы жағдайға байланысты
толқындық механикада мынадай принцип бар: элеткронның орнын
және импульсін біл мезгілде дәл өлшеуге болмайды, басқаша
айтқанда электронның координаттарын және жылдамдықтарын бір
мезгілде дәл өлшеу мүмкін емес.
Зат бөлшектерінің толқындық қасиеттері. Де
Бройль жорамалы
Оптикалық құбылыстардың көпшілігін ( дифракция,
интерференция)
жүйелі түрде толқындық көзқарас тұрғысынан
кескіндеуге болатын оптика курсынан белгілі. Ал
кейбір құбылыстарда (фотоэффект, Комптон
эффект) жарық өзінің корпускулалық табиғатын анық
байқатады.
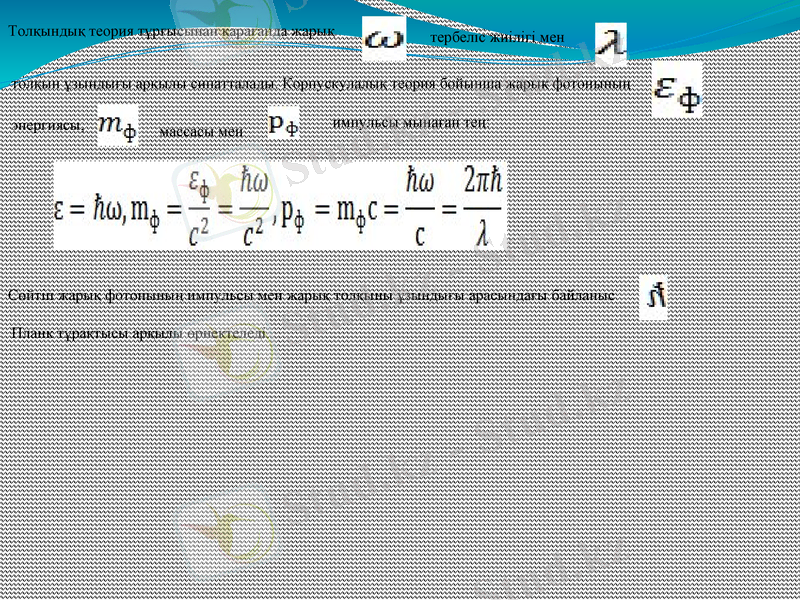
Толқындық теория тұрғысынан қарағанда жарық тербеліс жиілігі мен

толқын ұзындығы арқылы сипатталады. Корпускулалық теория бойынша жарық фотонының

энергиясы, импульсы мынаған тең:
массасы мен

Сөйтіп жарық фотонының импульсы мен жарық толқыны ұзындығы арасындағы байланыс

Планк тұрақтысы арқылы өрнектеледі.
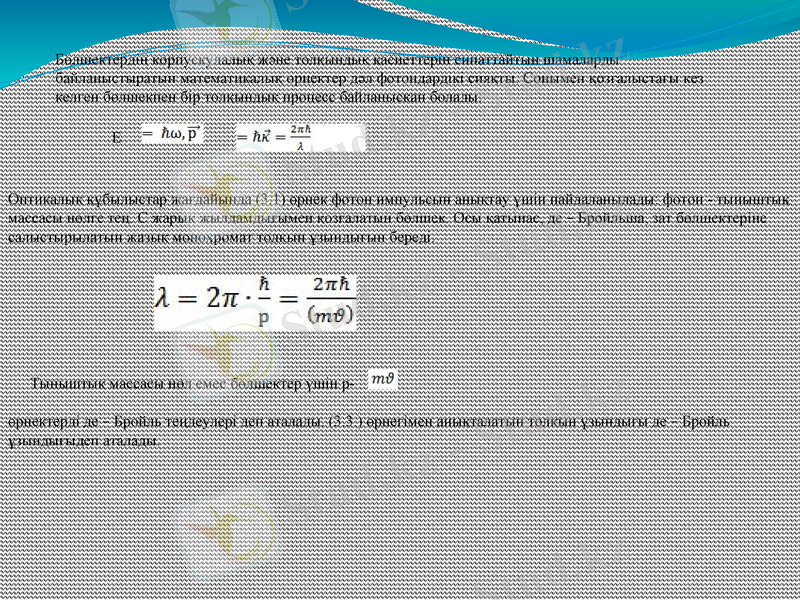
Бөлшектердің корпускулалық және толқындық қасиеттерін сипаттайтын шамаларды
байланыстыратын математикалық өрнектер дәл фотондардікі сияқты. Сонымен қозғалыстағы кез
келген бөлшекпен бір толқындық процесс байланысқан болады.

Е

Оптикалық құбылыстар жағдайында (3.1) өрнек фотон импульсын анықтау үшін пайдаланылады: фотон - тыныштық
массасы нөлге тең. С жарық жылдамдығымен қозғалатын бөлшек. Осы қатынас, де – Бройльша, зат бөлшектеріне
салыстырылатын жазық монохромат толқын ұзындығын береді.

Тыныштық массасы нөл емес бөлшектер үшін р-

өрнектерді де – Бройль теңдеулері деп аталады. (3.3.) өрнегімен анықталатын толқын ұзындығы де – Бройль
ұзындығыдеп аталады.
Зат бөлшектері толқындық қасиеттерінің тәжірибеде расталуы
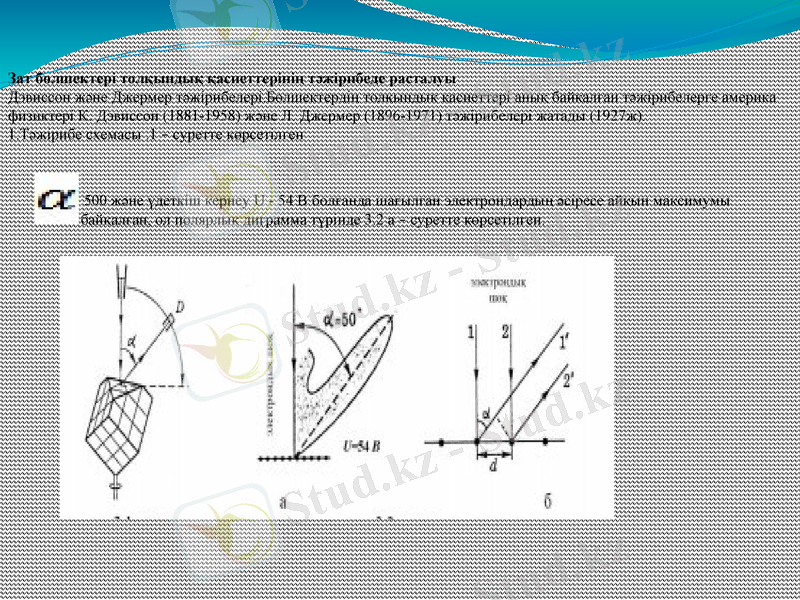
Дэвиссон және Джермер тәжірибелері.Бөлшектердің толқындық қасиеттері анық байқалған тәжірибелерге америка
физиктері К. Дэвиссон (1881-1958) және Л. Джермер (1896-1971) тәжірибелері жатады (1927ж).
1.Тәжірибе схемасы .1 – суретте көрсетілген

500 және үдеткіш кернеу U - 54 В болғанда шағылган электрондардың әсіресе айқын максимумы
байқалған, ол полярлық диграмма түрінде 3.2 а – суретте көрсетілген.
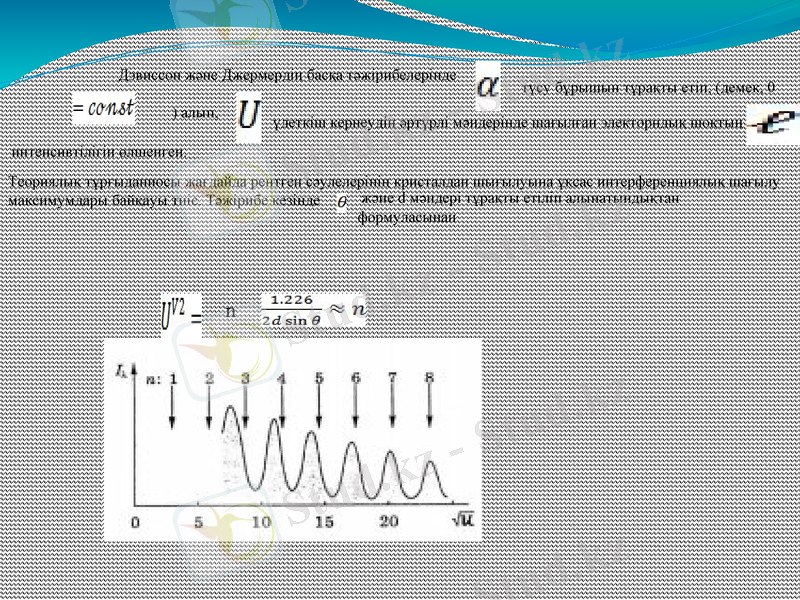
Дэвиссон және Джермердің басқа тәжірибелерінде
түсу бұрышын тұрақты етіп, (демек, 0
) алып,
үдеткіш кернеудің әртүрлі мәндерінде шағылған электорндық шоқтың
интенсивтілігін өлшенген.
Теориялық тұрғыданиосы жағдайда рентген сәулелерінің кристалдан шығылуына ұқсас интерференциялық шағылу
максимумдары байқауы тиіс. Тәжірибе кезінде және d мәндері тұрақты етіліп алынатындықтан
формуласынан

n

Ұқсас жұмыстар

Нанотехнологияға кіріспе. Нанотехнологиялардағы кванттық эффектілер

Коллоидты жүйелердің молекулакинетикалық және оптикалық қасиеттері

Кванттық физика тарихы және тарихи деректерді физика пәнін оқытуда қолдану әдістемесін оқыту

КВАНТ САНДАРЫ

Құрамында айнымалысы

Иммундық жүйе екі бөлікке бөлінген - гуморальдық иммунитет жүйесі және жасушалық иммунитет жүйесі

Атомның кванты - механикалық моделі

Толқындардың интерференция және дифракция құбылысы

Инерция моменті Инерция тензоры

Математикалық диктант

Пәндер