Кванттық ротатор

Презентация қосу

Кванттық ротатор
Ротатордың меншікті функциялары
Бұрыштық моменттің квадратының меншікті функцияларын
ротатордың, яғни материялық нүктенің сфера бойынша еркін
қозғалысының кванттық теориясын құрастыруға қолданалық.
Ротатор теориясының негізгі нєтижелерін екі атомды
молекулалардың спектрін зерттеуге пайдалануға болады.
Алдымен, жартылай кванттың Бор теориясындағы ротаторды
қарастырайық. Координаттар жүйесінің басын материалдық
нүкте қозғалатын радиусы r = a = constсфераның ортасына
орналастырайық. Бұл жағдайда потенциялық энергия тұрақты
болады:

U (r)U(a) = const
Ротатордың кванттық теориясын құрастыру барысында
бұл есептің орталық симметриялы өрістегі бөлшек
қозғалысының дербес жағдайы екендігін ескереміз.
Сондықтан, R(r ) - радиал функцияны анықтау үшін
мынадай теңдеуді пайдалана аламыз:
Ротатор үшін r = a = const болғандықтан Ñr2R(a) = 0, демек
(11.7) теңдеуден ротатордың энергиясы

Бұл өрнекті Бор теориясындағы ротатордың
энергиясы мен салыстырсақ, энергия EБор ал
кванттық теорияда екендігін көреміз .Бұл
айырмашылық M x M M z және бұрыштың
момент операторларының өзара коммутативті
емес екендігіне байланысты және ол кванттық
теорияның негізгі ерекшеліктеріне жатады.
Ротатордың энергиялық деңгейлерінің азғын болуы физикалық
тұрғыдан ротатордың орталық симметриялы жүйе болуының, яғни,
координаттар осінің басы арқылы өтетін барлық бағыттардың
бірінен бірінің айырмашылығы жоқ болуының салдары. Осы
тұрғыдан кез келген орталық – симметриялы жүйелердің
барлығында да азған күйлер болуы қажет.
Ал егер де жүйеде белгілі бір бағыт анықталған болса, мысалы,
сыртқы магнит өрісінің єсері, онда орталық симметрия
бүзылады, M бұрыштық моменттің барлық моменттері өзара
эквивалентті болмайды, яғни азғындық реті азаяды, не мүлдем
жойылады.Спектрлік терминологияда әртүрлі энергиялық деңгейлер
термдер деп аталады.
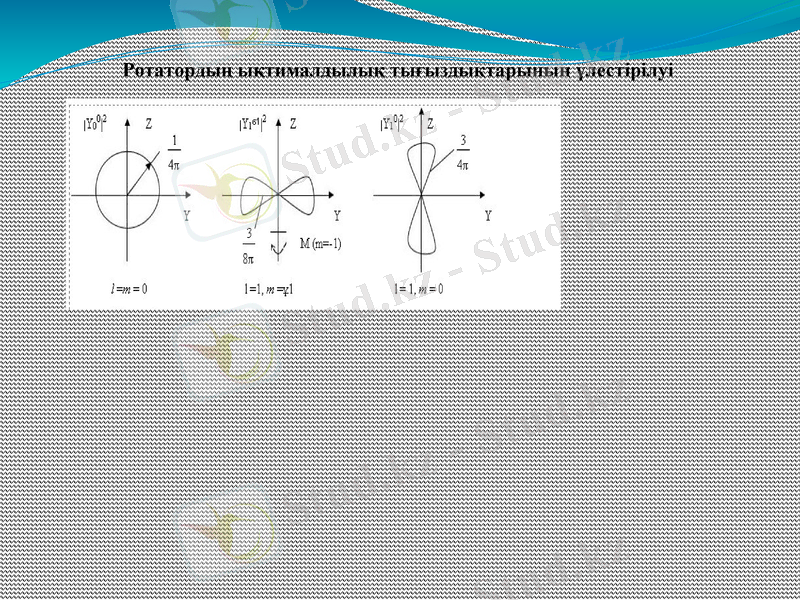
Ротатордың ықтималдылық тығыздықтарының үлестірілуі
Сұрыптау ережелері
Кванттық сандардың қандай өзгерістерінде кванттық өтулердің мүмкін болатындығын
анықтайтын сұрыптау ережелерін тағайындайтын матрицалық элементтер мынадай түрде
жазылады:

Егер кванттық сандардың кейбір өзгерістерінде (11.16)-
шыматрицалық элемент нольге тең болса, онда мұндай кванттық
өтулер тиым салынған болады (сәуле шығару болмайды). Сұрыптау
ережелері белгілі болса сєуле шығарудың жиілігі мен
қарқындылығын оңай есептеп шығара аламыз.
х, у жєнеz координаттарының орнына төмендегідей жаңа
айнымалылар енгізейік:
Z= a cosθ
ξ= x +iy =a sinθe
η = x −iy =a sinθe
iϕ
Екi атомды молекуланың айналыс спектрлерi.
Молекулалардың ядролары қатаң бекiтiлген деп ұйғарып айналыс спектрлерiн
қарастырайық. Бұл ротатор моделi, молекула құрамына кiретiн
массалары m және m атомдар қайсыбiр осьтi айналып қозғала алады. Атомдардың
инерция моментi бұлардың центрлерi арқылы өтетiн оське қатысты I=mr2-ге тең,
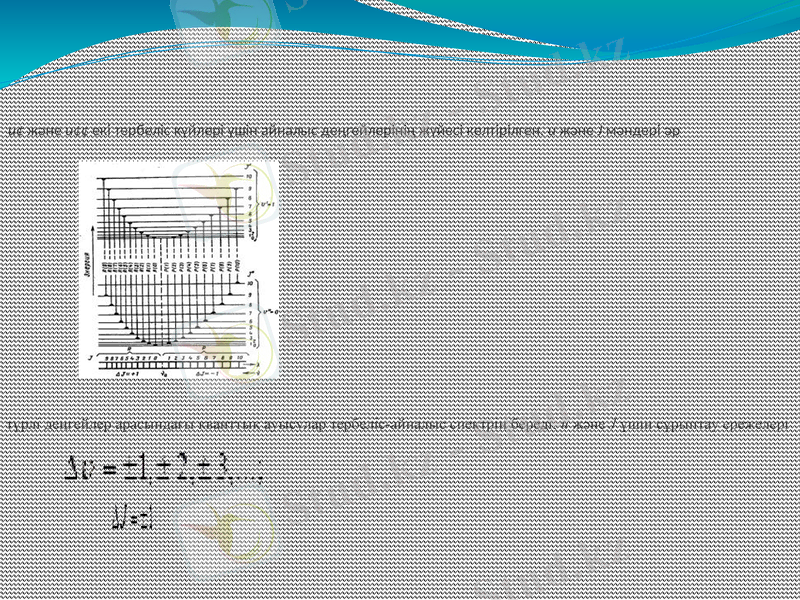
u¢ және u¢¢ екi тербелiс күйлерi үшін айналыс деңгейлерiнiң жүйесi келтiрiлген. u және J мәндерi әр

түрлі деңгейлер арасындағы кванттық ауысулар тербелiс-айналыс спектрiн бередi; u және J үшін сұрыптау ережелерi
Кванттық ротатор:
А) дененің радиусы а-ға тең сфера бетіндегі еркін қозғалысы

Кванттық ротордың толқындық
функциялары Ψlm(a,θ,φ)=R(a)∙Ylm(θ,φ) бірге нормалануы тиіс.
R радиалды функция үшін дұрыс қатынастар:
B) hπ∫0∞R*r 2dr=1 D) ∫Ψlm*Ψl`mdV =бll`бmm` G)∫Ψlm*ΨlmdV=1

Ұқсас жұмыстар

Кванттық физика тарихы және тарихи деректерді физика пәнін оқытуда қолдану әдістемесін оқыту

Кванттық мханикадағы тәжіриблер

Сөз құрамы

Физикалық шамалардың операторлары

Атомның кванты - механикалық моделі

Сәуле шығарғыштық қабілеті

КВАНТ САНДАРЫ

Нанотехнологияға кіріспе. Нанотехнологиялардағы кванттық эффектілер

Сәуле шығару энергиясы

ҚАЗІРГІ ЗАМАНҒЫ ФИЗИКА

Пәндер