ОРТАША ШАМАЛАР ЖӘНЕ ВАРИАЦИЯ КӨРСЕТКІШТЕРІ

Презентация қосу

ОРТАША ШАМАЛАР ЖӘНЕ
ВАРИАЦИЯ КӨРСЕТКІШТЕРІ

1.Орташа шаманың мәні мен маңызы
және оның қолданылу шарттары.
2. Арифметикалық орташа шама.

3. Құрылымдық орташа шамалар.

4. Вариация көрсеткіштері
«Каждый понимает, что такое
средние до тех пор, пока не начнет
применять их».
У.Дж.Рейхман.
ОРТАША ШАМА
Орташа шама деп –
статистикада жиынтықтың
бір бірлігіне есептелген
өзгермелі белгінің типтік
деңгейін сипаттайтын
жалпылама көрсеткішті
айтады.
Орташа шама құбылыстардың заңдылықтарын
және олардың ортақ қасиетін сапасына сай
сипаттау үшін келесі талаптар қойылады:
Орташа шамалар тек қана сапа жағынан

біртектес жиынтықтар негізінде есептелуі керек.
Жалпы орташаларды топтастыру әдісін

қолданып топтық орташалармен толықтыру
қажет.
Зерттелінетін құбылыстарды жан-жақты

талдау үшін бірнеше көрсеткіштер бойынша
орташа шамаларын есептеу қажет, яғни
орташалар жүйесін қолдану қажет.
Орташа шамалар зерттелінетін құбылыстардың

экономикалық табиғатын сипаттайтын қатынас
арқылы анықтауы қажет.
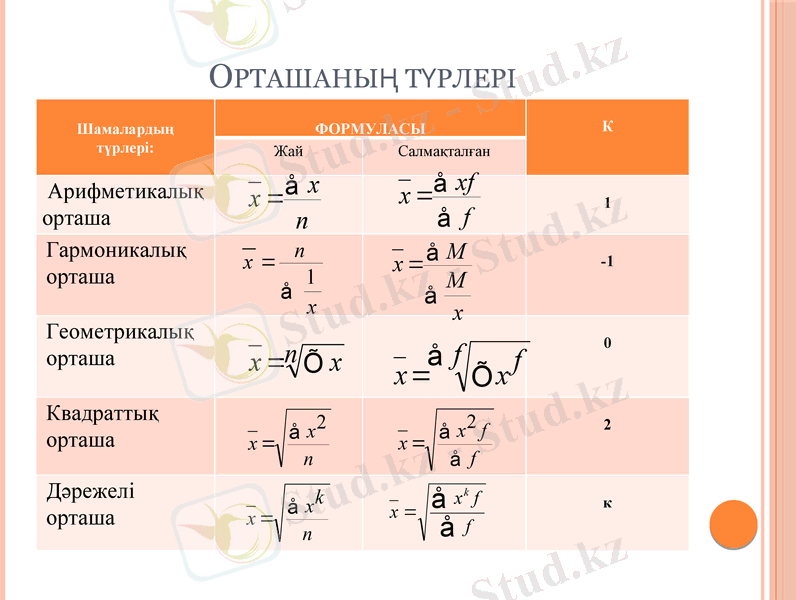
ОРТАШАНЫҢ ТҮРЛЕРІ
Шамалардың ФОРМУЛАСЫ К
түрлері: Жай Салмақталған

xf
Арифметикалық x
x x
орташа n f 1

n M
Гармоникалық x x -1
орташа 1 M

x x
Геометрикалық
орташа x n x f f
0
x x
Квадраттық 2 2 2
x x f
орташа x x
n f
Дәрежелі x f
xk
k
к
орташа x x
n f
ОРТАШАНЫҢ МАЖОРАНТТЫҒЫ
(М)

X X X X ... X k
гарм геом ариф квад
ОРТАША ШАМАНЫ ЕСЕПТЕУ ҮШІН
«ОРТАШАНЫҢ НЕГІЗГІ ҚАТЫНАСЫ» ДЕГЕН
ПРИНЦИПТІ ҚОЛДАНАДЫ.

Еңбек ақы қоры
Орташа еңбек ақы = -------------------------
Жұмысшы саны

Жалпы өнім
Орташа өнімділік = --------------------------
Егіс көлемі

Өнім көлемі
Орташа қор қайтымдылығы =
-----------------------------------
Негізгі қордың құны
ОРТАШАНЫҢ ФОРМУЛАСЫН ҚОЛДАНУ
1. Гармоникалық орташаның формуласын
қолдану шарттары:
а) Егер көрсеткіштің жеке мәндерінің
қосындысын анықтау мағынасыз болса, ал ол
жеке мәндерінің кері шамаларын қосу мүмкін
болса;
б) Егер орташаның негізгі қатынасындағы
алымы белгілі болып, бөлімі белгісіз болса.
Мысал: 10 сағаттық жұмыс күнінде төрт жұмысшы
бір нұсқадағы бас киім тігумен айланысады.
Бірінші жұмысшы бір бас киім тігуге 30 мин,
екіншісі – 40 мин, үшіншісі – 50 мин, төртіншісі –
60 мин жұмсайды. Орта есеппен бір бас киім тігуге
жұмсалатын уақыт мөлшерін есептеу керек.
ОЛ ҮШІН БАРЛЫҚ БАС КИІМГЕ ЖҰМСАЛҒАН УАҚЫТ
МӨЛШЕРІН ЖАЛПЫ БАС КИІМДЕРДІҢ САНЫНА БӨЛЕМІЗ.
Әрбір жұмысшы 600 минуттан (60 * 10 = 600) жұмыс
істеді. Ал төрт жұмысшы жалпы жұмыс уақыты 2400
минут (600 * 4 = 2400). Онда жалпы бас киім саны 57
дана болады.
(600/30 + 600/40 +600/50 + 600/60) = 57
Бір бас киімге жұмсалған орташа уақытты
гармоникалық орташаның салмақталған
формуласымен есептейміз:
ā = (600+600+600+600)/(600/30+600/40+600/50+600/60) =
= 2400/57 ≈ 42 мин.
Бұл мысалдағы жұмысшылардың барлығы бірдей уақыт жұмыс
істегендіктен гармоникалық орташаның жай формуласын
қолдануға болады:
ā = (1+1+1+1)/(1/30 + 1/40 + 1/50 + 1/60) ≈ 42 мин.
ОРТАШАНЫҢ ФОРМУЛАСЫН
ҚОЛДАНУ
2. Геометрикалық орташаның формуласын
қолдану шарттары:
а) Егер көрсеткіштің жалпы мәні оның жеке
мәндерінің көбейтіндісі түрінде анықталатын
болса.
ОРТАШАНЫҢ ФОРМУЛАСЫН
ҚОЛДАНУ
3. Арифметикалық орташаның
формуласын қолдану шарттары:
а) Егер орташа шамасын
есептейтін көрсеткіштің жиынтық
бойынша жалпы мөлшері оның
жеке мәндерінің қосындысы
арқылы анықталатын болса;
б) Егер орташаның негізгі
қатынасының бөліміндегі
шамалар белгілі болса, ал алымы
белгісіз болса.
АРИФМЕТИКАЛЫҚ ОРТАШАНЫ ЕСЕПТЕУДІҢ
ПРАКТИКАДАҒЫ НЕГІЗГІ ЖАҒДАЙЛАРЫ:
1. Статистикалық бақылаудың
нәтижесінде белгінің жеке мәндері
алынған. Барлық жеке мәндеріні
қосып олардың санына бөлеміз, яғни
арифметикалық орташаның жай
формуласы қолданылады.
2. Белгінің жеке мәндері берілмеген,
бірақ, жеке мәндердің қосындысы
берілген және жиынтық
бірліктерінің саны берілген.
АРИФМЕТИКАЛЫҚ ОРТАШАНЫҢ ЕСЕПТЕУДІҢ
ПРАКТИКАДАҒЫ НЕГІЗГІ ЖАҒДАЙЛАРЫ:
3. Таратпалы қатардың мәліметтері бойынша
орташаны есептеу.
3.1. Дискреттік таратпалы қатардың
мәліметтері бойынша орташаны есептеу үшін,
алдымен варианттарды жиіліктерге көбейтіп
аламыз, сол көбейтінділердің қосындысын
жиіліктердің қосындысына бөлеміз, яғни
арифметикалық орташаның салмақталған
формуласын есептейміз.
3.2. Интервалдық таратпалы қатардың
мәліметтері бойынша орташаны есептеу үшін
алдымен әрбір интервалдың ортасын тауып
аламыз. Содан кейін дискреттік таратпалы
қатардың мәліметтері сияқты есептейміз.
АРИФМЕТИКАЛЫҚ
ОРТАШАНЫҢ
МАТЕМАТИКАЛЫҚ ҚАСИЕТТЕРІ
1. Тұрақты шаманың орташасы оның
өзіне тең:
A A
2. Орташаның жиіліктердің
қосындысына көбейтіндісі варианттар
мен жиіліктердің көбейтіндісінің
қосындысына тең. f - жиіліктер

x f xf
АРИФМЕТИКАЛЫҚ ОРТАШАНЫҢ
МАТЕМАТИКАЛЫҚ ҚАСИЕТТЕРІ
3. Әрбір вариантты белгілі бір тұрақты шамаға
өзгертсек, онда орташа да сол шамаға
өзгереді.

x A x A
4. Әрбір вариантты белгілі бір тұрақты шама есе
өзгертсе, онда орташа да сонша есе өзгереді.

Ax A x
АРИФМЕТИКАЛЫҚ ОРТАШАНЫҢ
МАТЕМАТИКАЛЫҚ ҚАСИЕТТЕРІ
5. Жиіліктердің әрқайсысын белгілі бір
тұрақты шама есе өзгертсе, одан орташа
өзгермейді.
x Af xf x
Af f
6. Барлық варианттардың орташадан
ауытқуларының алгебралық
қосындысы нөлге тең болады.

x x f 0
АРИФМЕТИКАЛЫҚ ОРТАШАНЫҢ
МАТЕМАТИКАЛЫҚ ҚАСИЕТТЕРІН
ҚОЛДАНЫП АРИФМЕТИКАЛЫҚ
ОРТАШАНЫ, МОМЕНТТІК ТӘСІЛМЕН
ЕСЕПТЕУГЕ БОЛАДЫ.
Олүшін алдымен 1-ші дәрежелі
моментті есептейміз –
x a
d f
m1 ;
f
x m1 d A
ҚҰРЫЛЫМДЫҚ ОРТАША
Статистикада мода деп – берілген
жиынтықта ең жиі кездесетін белгінің
мәнін айтамыз.
Дискреттік қатардың мәліметтері
бойынша мода белгінің ең үлкен
жиілігіне сәйкес мәні болады.
Интервалдық таратпалы қатардың
мәліметтері бойынша моданы анықтау
үшін алдымен модалық
интервалды анықтап аламыз, ол ең
үлкен жиілікке сәйкес болады. Содан
кейін сол интервалдың шегінде моданы
келесі формуламен есептейміз
МОДА

f мо f мо 1
М о Х мо h ;
f мо f мо 1 f мо f мо 1
M o мода ,
X MO модалык интервалды н томенгі шегі;
f MO модалык интервалды н жиiлiгi,
f MO -1 модалык интервалды н алдындагы жиiлiгi,
f MO 1 модалык интервалда н кейiнгi жиiлiгi;
h - интервалды н шамасы.
МЕДИАНА

Медиана деп реттелген
қатардың дәл ортасында тұрған
вариантты айтамыз. Яғни
медиана берілген жиынтықты
белгінің мәндері бойынша теңдей
екі бөлікке бөледі.
ТАРАТПАЛЫ ҚАТАРДЫҢ МӘЛІМЕТТЕРІ
БОЙЫНША МЕДИАНАНЫ ЕСЕПТЕУ:

1.Дискретті қатардың мәліметтері
бойынша медиананы анықтау үшін
алдымен жиынтық
жиіліктерді (S) есептеп аламыз.
Содан кейін жиіліктің
қосындысының жартысына (∑f/2) тең
немесе одан үлкен жиынтық
жиілікке сәйкес белгінің мәнін
(вариантты) медиана деп аламыз.
ТАРАТПАЛЫ ҚАТАРДЫҢ МӘЛІМЕТТЕРІ
БОЙЫНША МЕДИАНАНЫ ЕСЕПТЕУ:
2. Интервалдық қатардың мәліметтері
бойынша медиананы анықтау үшін
алдымен медианалық
интервалды анықтаймыз.
Жиіліктердің қосындысының
жартысына (∑f/2) тең немесе одан
үлкен жиынтық жиілікке (S) сәйкес
интервалды медианалық интервал
деп аламыз. Содан кейін медиананы
мына формуламен есептейміз:
МЕДИАНА

f S Me 1
M e X Me h 2
f me
f жиiлiктердiнкосындысынынжартысы
f Me медианалыкинтервалдынжиiлiгi
S Me 1 медианалыкинтервалдыналдындагыжиынтыкжиiлiк
X Me медианалыкинтервалдынтоменгiшегi
h интервалшамасы
МЫСАЛ: ЖҰМЫСШЫНЫҢ ЕҢБЕК СТАЖЫ
БОЙЫНША ТОПТАРЫ БЕРІЛГЕН:
Еңбек Жұмысшы
стажы, X лар саны, f
11 хар
x f
f
21 9
24 15
Барлығы: 100
1371
x 13,71
100
Еңбек Жұмысшыл хf S
стажы, x ар саны, f
3 15 45 15
6 7 42 22
9 11 99 33
12 16 192 49
15 14 210 63
18 13 234 76
21 9 189 85
24 15 360 100
Барлығы: 100 1371
Мода Медиана

f 50,
f Max 16, 2
Mo 12 S Me 63,
Me 15.
ВАРИАЦИЯ КӨРСЕТКІШТЕРІ
Вариация өрісі – белгінің
мәндерінің қандай аралықта
өзгеретіндігін сипаттайды. Оның
шамасы белгінің ең үлкен және ең
кіші мәндерінің айырмасына тең.

R Х max Х min
ОРТАША СЫЗЫҚТЫҚ АУЫТҚУ

Жай Салмақталған

d
(x x)
d
| x x| f
n f
ДИСПЕРСИЯ

Жай Салмақталған

(х х) 2

(х х) 2
f
п f
ОРТАША КВАДРАТТЫҚ АУЫТҚУ

(х х) 2

( x x) 2
f
п f
ВАРИАЦИЯ КОЭФФИЦИЕНТІ –
ОРТАША КВАДРАТТЫҚ
АУЫТҚУДЫҢ ОРТАША
ШАМАДАҒЫ %-ДЫҚ ҮЛЕСІН
КӨРСЕТЕДІ

V 100%
x
ВАРИАЦИЯ КӨРСЕТКІШТЕРІН
ЕСЕПТЕУ
Еңбек Жұмыс xf Х - Xорт |Х-Хорт| |Х-Хорт|f (Х - Xорт)^2 (Х - Xорт)^2*f
стажы, x шылар
саны, f
3 15 45 -10,71 10,71 160,65 114,70 1720,56
6 7 42 -7,71 7,71 53,97 59,44 416,11
9 11 99 -4,71 4,71 51,81 22,18 244,03
12 16 192 -1,71 1,71 27,36 2,92 46,79
15 14 210 1,29 1,29 18,06 1,66 23,30
18 13 234 4,29 4,29 55,77 18,40 239,25
21 9 189 7,29 7,29 65,61 53,14 478,30
24 15 360 10,29 10,29 154,35 105,88 1588,26
Барлығы 100 1371 587,58 4756,59
ВАРИАЦИЯ КӨРСЕТКІШТЕРІН
ЕСЕПТЕУ
Орташа: x = 1371/100 = 13,71
Орташа сызықтық ауытқу:
d = 587,58/100 = 5,88

Дисперсия: σ² = 4757/100 = 47,57
Отраша квадраттық ауытқу:
σ = √47,57¯ = 6,9
Вариация коэффициенті:
V = 6,9*100/13,72 = 50,30 %
ДИСПЕРСИЯНЫҢ
МАТЕМАТИКАЛЫҚ ҚАСИЕТТЕРІ:
1. тұрақты шаманың дисперсиясы 0-ге тең:
D(A) = 0;
2. белгінің жеке мәндерін бір тұрақты
шамаға өзгерткеннен дисперсия
өзгермейді:
D(X ± A) = D(X);
3. белгінің жеке міндерін бір тұрақты шама
есе өзгертсе, онда дисперсия сол шаманың
квадраты есе
2 өзгереді:
D( A X ) A D( x)
ДИСПЕРСИЯНЫҢ
МАТЕМАТИКАЛЫҚ ҚАСИЕТТЕРІ:
4. дисперсия белгінің мәндерінің
квадраттарының орташасы мен
орташаның квадратының айырмасына
тең:
2 2 2
x (х)

x 2

х 2

;х
х
п п
ДИСПЕРСИЯНЫ ЕСЕПТЕУДІҢ
МОМЕНТТІК ТӘСІЛІ
2 2 2
d (m2 m1 )
x A
d f
m1
f
x A 2
( d ) f
m2
f
ДИСПЕРСИЯ ТҮРЛЕРІ ЖӘНЕ
ДИСПЕРСПЕРСИЯЛАРДЫ ҚОСУ ЕРЕЖЕСІ

Дисперсияларды қосу
ережесі бойынша
2 2 2
жалпы дисперсия - i
топаралық дисперсия
мен топтық
дисперсиялардың
орташасының
қосындысына тең:
ЖАЛПЫ ДИСПЕРСИЯ

(у у) 2

п
2 2 2
у ( у)

( у у) 2
f
f
ТОПТЫҚ ДИСПЕРСИЯЛАР ЖӘНЕ
ОЛАРДЫҢ ОРТАШАСЫ

i
(y i yi ) 2

ni

n
i i

n
i
i
ТОПАРАЛЫҚ ДИСПЕРСИЯ

( у y)
i
ni
n i

Ұқсас жұмыстар

Вариациялық көрсеткіштер

Аралық қатардың үлестірімінің сандық сипаттамасы

Вариация көрсеткіштері

Абсолютті шамалар

Вариациялық қатардың түрлері

Өсіңкілік қатарлары

Өлшеулер және олардың геодезиялық және фотограмметрикалық жұмыстардағы мәні

Қаржылық тәуекелдерді талдау және бағалау

ДИНАМИКАЛЫҚ ҚАТАРЛАР

Бас жиынтық және таңдама. Таңдамалы сипаттамалар

Пәндер