Модельдеу объектісі

Презентация қосу

Математикалық модель
классификациясы

Әбдікәрім Әли
АУ-601
Жоспар:
1.Модельдеу мақсатына байланысты жіктеу.
2.Модельдеу объектісінің күрделілігі бойынша
жіктеу.
3.Модель операторына байланысты жіктелуі.
4.Қолданылатын параметрлеріне байланысты
жіктелуі.
Математикалық модельдер өте көп. Оларды мына
параметрлер бойынша жіктеуге болады:
• Модельдеудің мақсаттары.
• Модельдеу объектісінің күрделілігі;
• Модель операторы (қосалқы үлгілер);
• Кіріс және шығыс параметрлері;
• Моделді зерттеу әдісі;
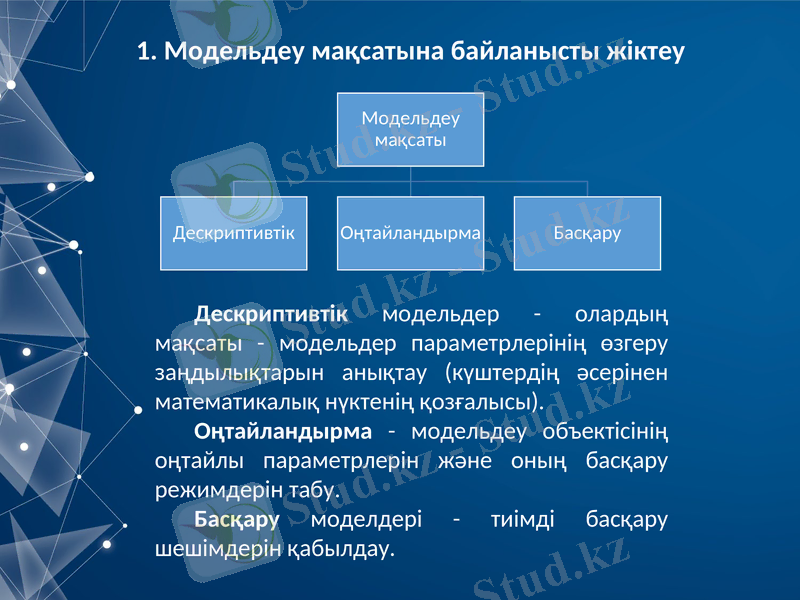
1. Модельдеу мақсатына байланысты жіктеу

Модельдеу
мақсаты

Дескриптивтік Оңтайландырма Басқару

Дескриптивтік модельдер - олардың
мақсаты - модельдер параметрлерінің өзгеру
заңдылықтарын анықтау (күштердің әсерінен
математикалық нүктенің қозғалысы).
Оңтайландырма - модельдеу объектісінің
оңтайлы параметрлерін және оның басқару
режимдерін табу.
Басқару моделдері - тиімді басқару
шешімдерін қабылдау.
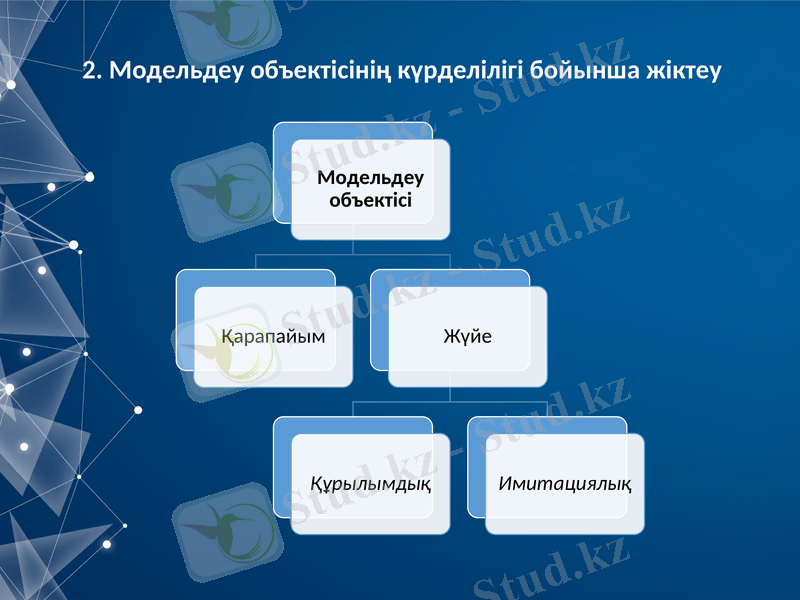
2. Модельдеу объектісінің күрделілігі
бойынша жіктеу

Модельдеу
объектісі

Қарапайым Жүйе

Құрылымдық Имитациялық
Модельдеу объектісі ретінде материалдық дене, конструкция, процесс, құбылыс алынуы
мүмкін. Барлық модельдеу объектілерін төмендегідей бөлуге болады:
• қарапайым;
• жүйелік нысандар.

Модельдеудің қарапайым объектілері құраушы элементтерге бөлінбейді, ішкі өзара
байланыс қарастырылмайды (математикалық нүкте).

Модельденетін объект-жүйе нысанның барлық құраушы элементтерін және олардың
арасындағы өзара байланысты қарастырады. Егер объектте n-элементтер болса, олардың
арасында n(n-1) өзара әрекеттесуі бар. Әрбір элементтің m-жағдайлары бар, онда
жағдайлардың жалпы саны S=mn болады.

Жүйелік нысандар:
• Құрылымдық;
• Имитациялық болуы мүмкін.

Құрылымдық модельдер - жеке элементтердің іс-әрекеті мен қасиеттерін және олардың
арасындағы қатынастарды ескеретін модельдер.

Имитациялық модельдер - элементтер мен жағдайлардың соңғы саны бар модельдер.
Жүйедегі элементтердің өзара әрекеттесуін модельдеу ЭЕМ алгоритмдері арқылы жүзеге
асырылады.
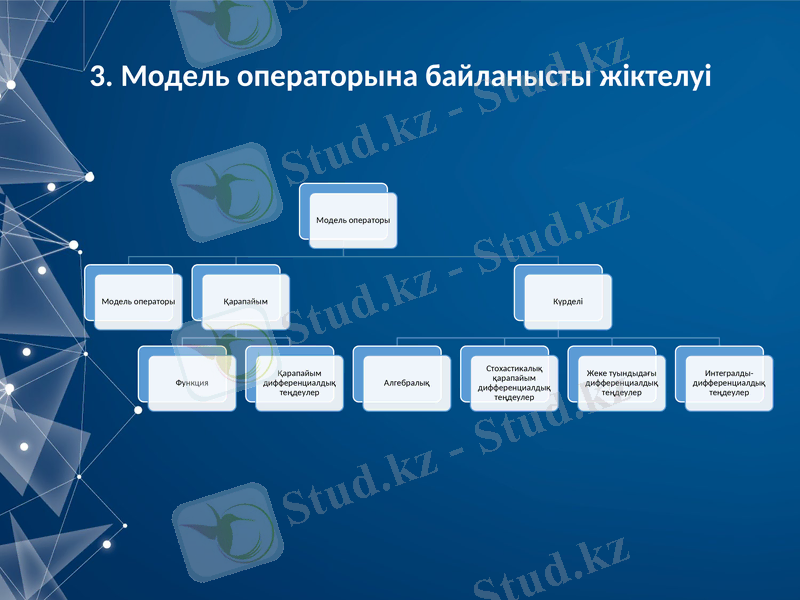
3. Модель операторына байланысты
жіктелуі

Модель операторы

Модель операторы Қарапайым Күрделі

Стохастикалық
Қарапайым Жеке туындыдағы Интегралды-
қарапайым
Функция дифференциалдық Алгебралық дифференциалдық дифференциалдық
дифференциалдық
теңдеулер теңдеулер теңдеулер
теңдеулер
Сызықтық модельдер - y шығыс мәндері x кіріс мәндеріне
байланысты болатын модельдер. Сызықтық модельдер ең
қарапайым болып табылады.

Сызықты емес модельдер сызықтыға қарағанда күрделі және
перспективалы. Сызықты емес модельдерді пайдалана отырып, ең
күрделі объектілерді, процестерді, құбылыстарды сипаттауға
болады.

Математикалық модельдің оператор түріне байланысты:
•- қарапайым;
•- күрделі.

Қарапайым модельдер - сызықтық модельдер - y шығыс
мәндерінің x мәндеріне (Ом заңы) тәуелділігін орнатуға болатын
модель.

Күрделі математикалық модельдер - бұл дифференциалды
және интегралдық қатынастарды пайдаланатын және күрделі
математикалық әдістерді қолдануды талап ететін модельдер.
4. Қолданылатын параметрлеріне байланысты жіктелуі.

Математикалық модельде қолданылатын параметрлер жиынтығының
түрлеріне байланысты төмендегідей бөлінеді:
•Дискретті (үзілмелі);
•Үздіксіз;
•Аралас;
•Сапалық;
•Сандық.

Математикалық модель параметрінің белгісіздік сипаттамасына
сәйкес келесідей модельдер болады:
•детерминирленген - параметрлердің мәндері санға сәйкес келеді;
•Стохастикалық - параметрлер ықтималдық тығыздығына байланысты
кездейсоқ айнымалы мәндерге сәйкес келеді;
•кездейсоқ - ықтималдық тығыздығының бағалауларымен берілген
кездейсоқ шамаларға сәйкес келетін параметрлердің мәндері;
•интервалды - параметрлердің мәндері сандар аралығымен
белгіленеді;
•анық емес - параметр мәндері анық емес жиынтыққа қатысты
функциялармен сипатталады.
Кеңістікке қатысты математикалық модельдер болуы
мүмкін (модельдің параметрлеріне координаталар кіреді):
• бір өлшемді;
• екі өлшемді;
• үш өлшемді.

Уақытқа қатысты:
• Динамикалық - сыртқы әсерлер мен күйлердің
параметрлерінің өзгеруі үлкен, уақытты есепке алу қажет
• стационарлы - параметрлерінің кішкене ауыспалы
мәндерінде уақытқа тәуелді емес (құбыр арқылы ағатын су
ағыны).
• тұрақсыз - маңызды тәуелсіз айнымалылардың бірі –
уақыт (құбыр арқылы ыдысқа ағатын су ағыны).

Ұқсас жұмыстар

Болашақ мұғалімдерді ақпараттық- компьютерлік және математикалық модельдеу негізінде кәсіби дайындау жүйесі

Блок - сызбада циклдік алгоритмнің шарты

Болашақ мұғалімдерді ақпараттық-компьютерлік және математикалық модельдеу негізінде кәсіби дайындау жүйесі туралы

Моделдеу мақсаты

Қаржы тәуекелдерін тиімділігін бағалау

Мектептегі информатика курсында

Теориялық зерттеу әдістері

Фразеологиялық тіркестер

Биологиялық мониторинг

ӘДІСТЕМЕ ОБЪЕКТІСІ

Пәндер