Интегралдаудың негізгі әдістері: тікелей интегралдау, айнымалыны алмастыру және бөліктеп интегралдау



11. 4. Интеграциялаудың
негізгі қасиеттері
1. Тікелей интегралдау
Тікелей интегралдау деп кестеде келтірілген анықталмаған интегралдар мен анықталмаған интегралдардың негізгі қасиеттерін қолданып алғашқы функцияларды табу.

Мысалдар.
Интегралды анықтау:
1
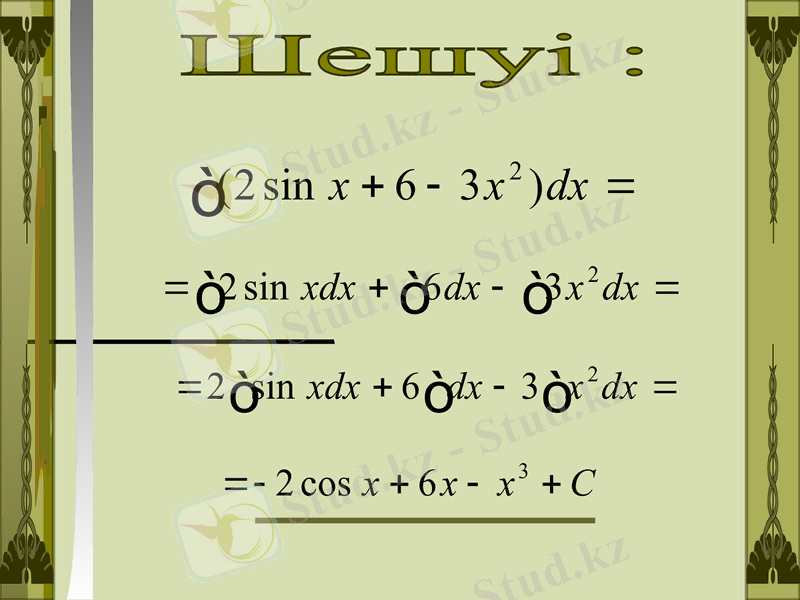
Шешуі :
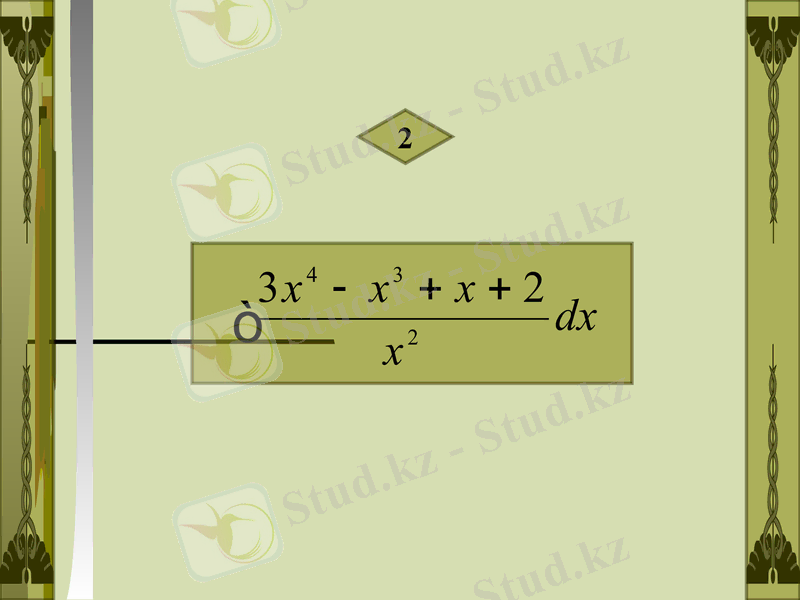
2

Шешуі :
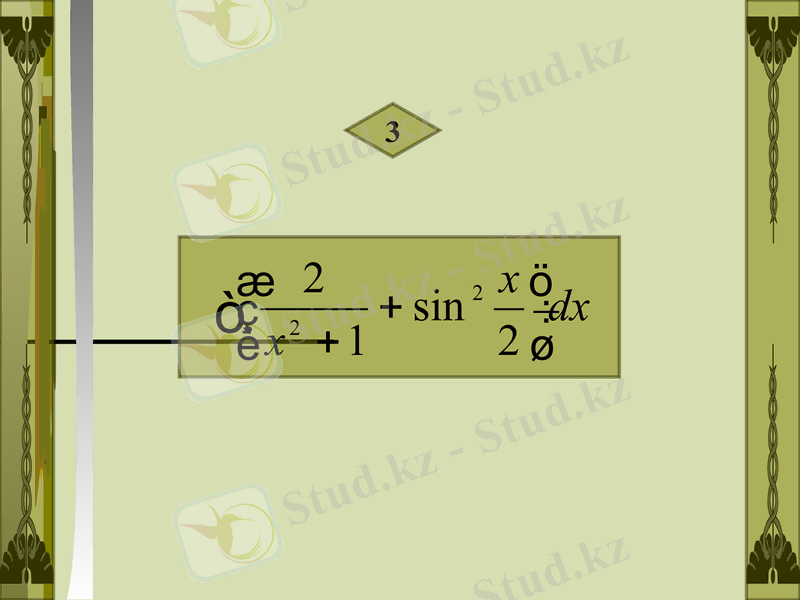
3

Шешуі :

2. Айнымалыны алмастыру
немесе ауыстыру әдістері
Айнымалыны алмастыру әдісі келесі формула түрінде жазылады:
1

Айнымалыны алмастыру әдісі

Қарастырылған аралықта дифференциалданатын х=φ(t) - функциясы.
Осы формуланың әділдігін көрсетейік. Оң жағына сол жағынан t-ға қатысты туындыны тауып көрейік (1) :

Бірдей нәтиже алдық, демек Лагранжа теоремасының нәтижесінде өрнектің сол және оң жағы (1) кейбір тұрақтылыққа ажыратылады.
Анықталмаған интегралдар өздері еркін тұрақты мерзімге дейін анықталғаннан бастап, содан кейін осы тұрақтыны төмендетуге болады.

Алынған формула жаңа айнымалыға көшу кезінде, интеграл астындағы өрнектің айнымалысын ауыстыру жеткілікті.
Айнымалыны ауыстыру бастапқы интегралды жеңілдетуге мүмкіндік береді және кейбір жағдайларда кестелік түрге әкеледі.

Мысалдар .
Интегралды анықтау:
1

Шешуі :
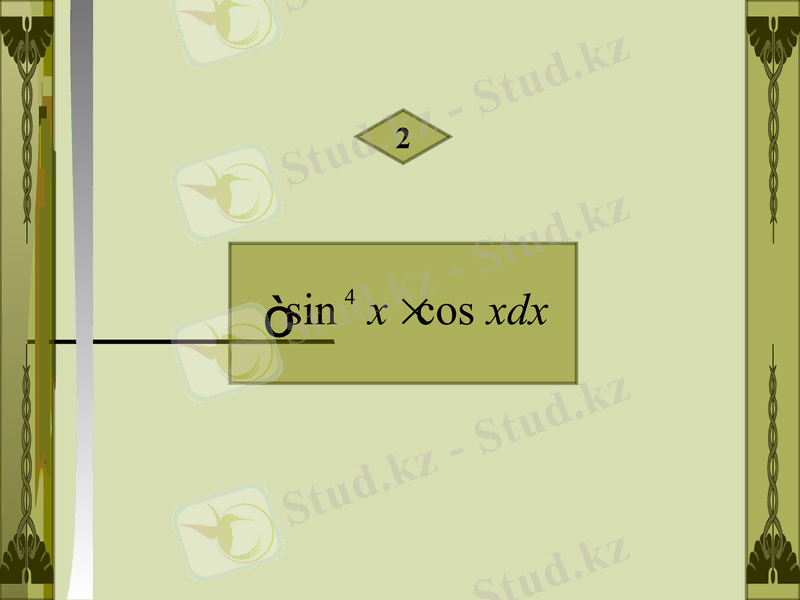
2

Шешуі :

Теорема.
F(x) функциясы - кейбір f(x) функциясы үшін алғашқы функция.
Сонда

Мысалдар .
Интегралды анықтау:
1
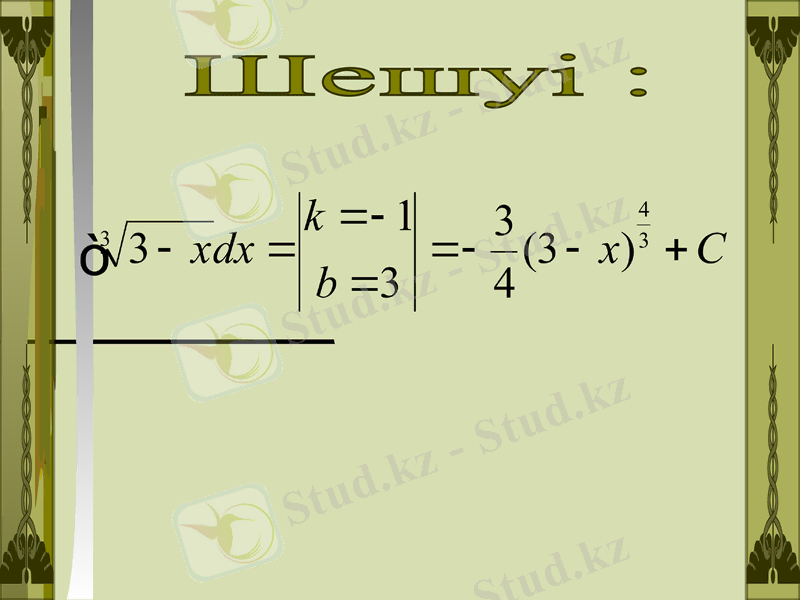
Шешуі :
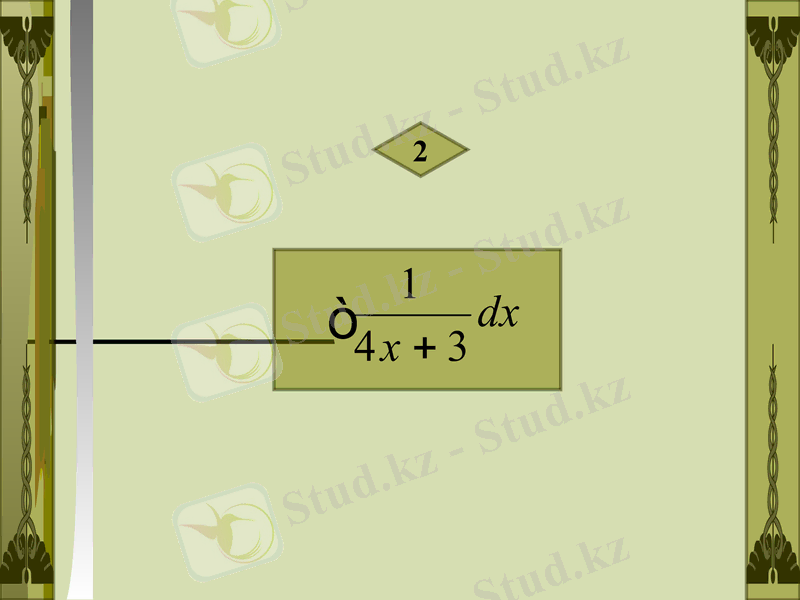
2

Шешуі :

3Бөліктеп интегралдау
u(x) және v(x) функциялары бір Х аралығында анықталған дифференциалданатын функциялар болсын, сонымен қатар осы аралықта
функциясының алғашқы функциясы бар болсын.
Теорема.
.

Х аралығында
функциясының да алғашқы функциясы бар және төмендегі формула орындалады.
Сонда

Дәлелдеу:
Функцияның туындысын табайық :
Осыдан, өрнектін оң жағындағы екінші өрнегін табайық:

Өрнектің оң жағы Х аралығында теореманың шарты бойынша алғашқысына ие, демек, өрнектің сол жағы да алғашқысына ие және теңдікті интегралдау кезінде, келесіге ие болады :

Демек,
Онда, соңғы теңдік келесідей түрде жазылады:
Бөліктеп интегралдау
формуласы

мысалдар.
Интегралды анықтау:
1

Шешуі :
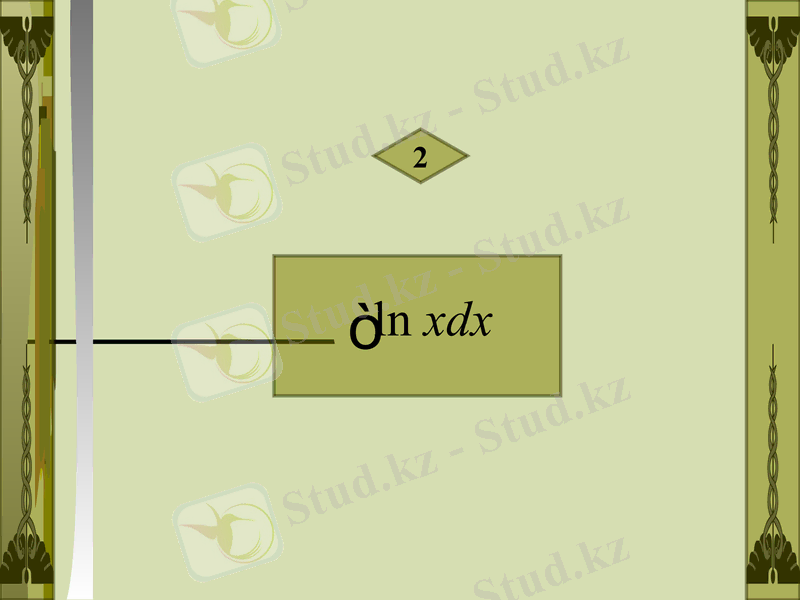
2
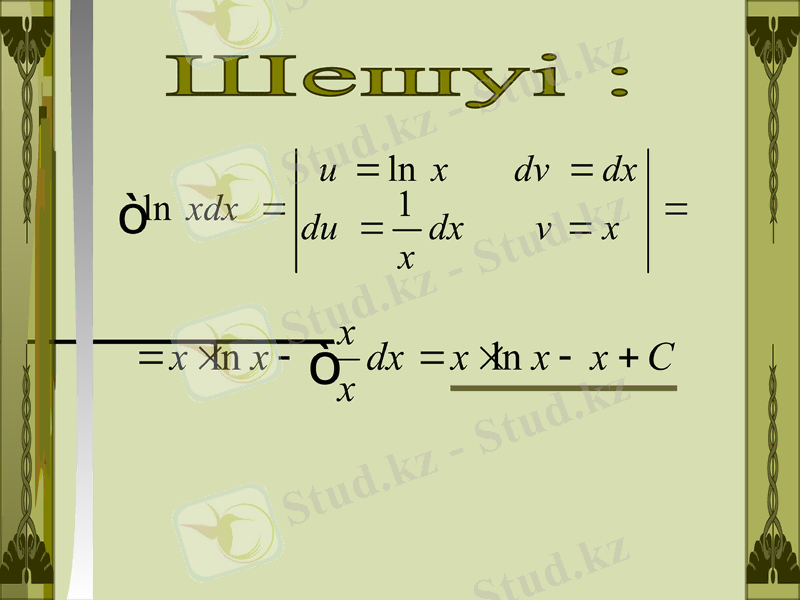
Шешуі :
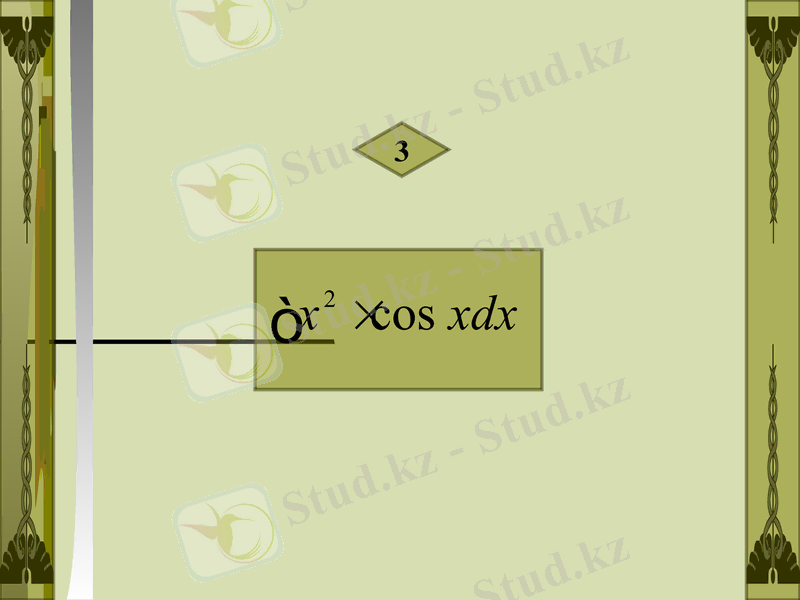
3

Шешуі :
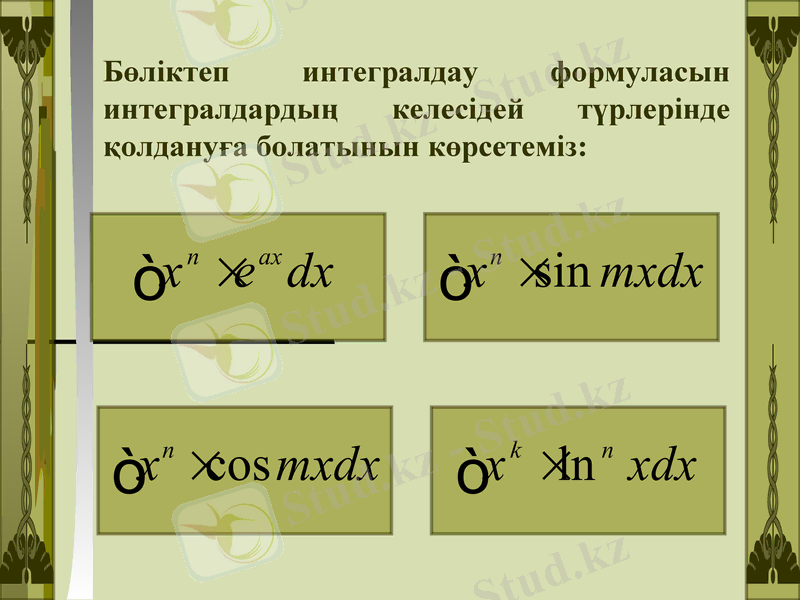
Бөліктеп интегралдау формуласын интегралдардың келесідей түрлерінде қолдануға болатынын көрсетеміз:

a, m, k - нақты сандар, n - бүтін оң сон.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz