Функцияны толық зерттеу және графигін құрастыру: анықталу облысы, жұптық, асимптоталар, монотондық, экстремумдер және дөңестілік

Скачать

1

Анықталу облысын табу.

2

Функцияның жұп және периодты екендігін

зерттеу.

3

Вертикальды асимптоттарды табу.

4

Функцияның горизонтальды

немесе көлбеу асимптоталарын зерттеу.

5

Функцияны экстремумге және монотондыққа

зерттеу.

6

Функция графигінің

дөңестік пен ойыстық аралықтарын

және иілу нүктесін

табу.

7

Функцияның кей нүктелеріндегі мәндерін

есептеп табу керек (функция графигінің дәлдігін

күшейте түсу үшін неғұрлым көбірек

мәндерді есептеген дұрыс)

мысал.

Функцияны зерттеу және

оның графигін салу

ШЕШУІ:

1

Функцияның анықталу облысын табамыз.

Функция х-тың барлық мәндерінде анықталған

Функцияның анықталу облысы интервалдармен біріктіріледі:

2

Функцияның жұптығын және периодтылығын зерттеу:

-ден басқа

Функцияның графигі ордината осіне симметриялы болса, функция жұп болады.

Функция периодты емес.

3

Вертикальды асимптоталарды іздейміз.

Вертикальды асимптоталар функцияның үзілген нүктесінде болуы мүмкін х =1 және х = -1.

Алдымен х=1 нүктесін қарастырамыз.

Егер шектердің біреуі

шексіздікке тең болса, х =1 түзуі вертикальды асимптота болады.

Сол жағы

Оң жағы

х=1 түзуі вертикальды асимптота.

х=-1 түзуі ординат осіне симметриялы болғандықтан, функция графигі вертикальды асимптота болады.

4

Функцияны шексіздікке зерттейміз де, горизонтальды және көлбеу асимптоталарды іздейміз.

болғанда

болғанда

y=-1 - горизонтальды асимптота.

Көлбеу асимптота жоқ.

5

Функцияның экстремумын және интервалдардың монотондылығын іздейміз.

Ол үшін бірінші туындыны табамыз:

болғандықтан

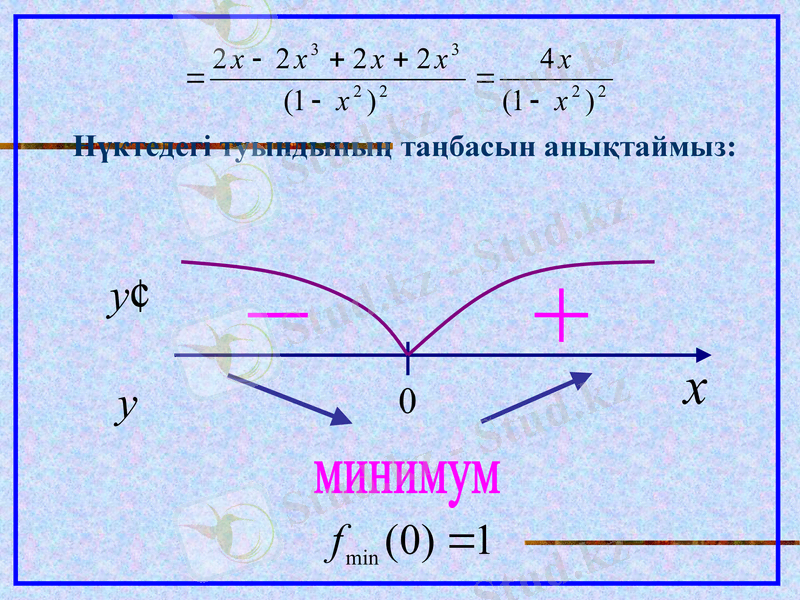
Нүктедегі туындының таңбасын анықтаймыз:

минимум

Функцияның монотонды интервалдары :

Функция кемиді:

Функция өседі:

6

Дөңестілік интервалын және иілу нүктесін табамыз

Ол үшін екінші туындыны есептейміз:

Екніші туындының нөлге қарасты нүктелері болмағандықтан, графиктің иілу нүктесі де жоқ.

Алым әрқашан оң болғандықтан, екінші туындының таңбасы бөлгішпен анықталады.

Функцияның дөңестілік интервалы :

Функцияның төмен дөңесі:

Функцияның жоғары дөңесі:

7

Функция графигінің координат осімен қиылысу нүктесін табамыз:

(0, 1) - ординат осімен қиылысу нүктесі.

Абсцисса осімен қиылысу нүктесі жоқ.

8

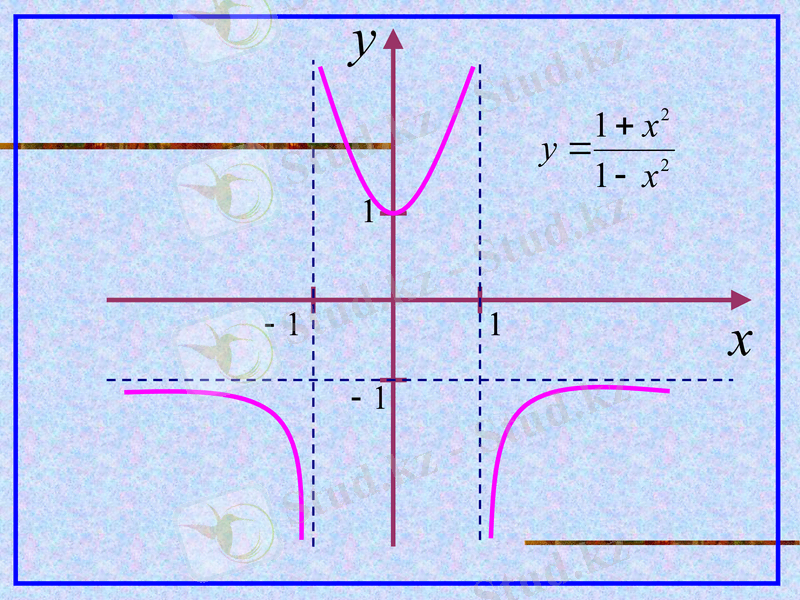
Функцияның графигін саламыз:

маңында

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс