Математика пәнінің мұғалімі

Презентация қосу

Түркістан қаласы
Ж.Еділбаев атындағы №18 мектеп-гимназия мемлекетттік
коммуналдық мекемесі.
Математика пәнінің мұғалімі
Полатбаева Айнұр
Түркістан қаласы, Бекзат мөлтек ауданы
Жұмабек Еділбаев №18 атындағы
мектеп-гимназиясы
Аты-жөні:Полатбаева Айнұр Өтегенқызы
Кәсіби тәжірибесі:13 жыл
Қызмет ететін мекемесі: №18 Ж.
Еділбаев атындағы мектеп-гимназиясы
Қазіргі лауазымы мен қызметі:
математика пәнінің мұғалімі
Оқытатын оқушыларына қысқаша
шолу: 5-11 сынып оқушыларына қазақ
тілінде сабақ жүргіземін.
I.Кіріспе
Тарихи мағлұматтар.
II.Негізгі бөлім:
2.1. Жазық фигуралардың ауданын
табуда анықталған интеграл қолдану
2.2. Параболамен және түзумен
шектелген әрі боялған фигураның
ауданын есептеудің әдістері.
2.3. Өтілген сабақ үлгілері.
ІІІ.Қорытынды
ІV.Қолданылған әдебиеттер.
• Тарихи мағұлматтар
• Интеграл ұғымы кез келген жазық фигуралардың ауданын, сондай-ақ кез
келген дене бетінің ауданын және көлемін есептеу қажеттілігінен пайда болды.
• Мәселен, Ежелгі Грекия мен Римде матемаик ғалымдар кез келген жазық
фигураның квадратурасын (тең шамалы квадрат салу тәсілмен ауданды табу)
және кез келген дененің кубатурасын (тең шамалы куб салу тәсілмен көлемді
табу) табуға есептер шығарумен айналысқан. Олар өз есептеулерінде Е в д о к с
К н и д с к и й (шамамен б.з.д. 408-358 жылдар) ұсынған түгесу (аяқтау, тауысу)
әдісін қолданған. Мысалы, бұл әдісті қолдану арқылы Евдокс екі дөңгелектің
аудандарының қатынасы олардың диаметрлері квадраттарының қатынасына,ал
табаны мен биіктігі цилиндрдікіндей болатын конустың көлемі цилиндр көлемінің
бөлігіне тең екенін дәлелденген.
• Архимед өзінің «Парабола квадратурасы» шығармасында Евдокс әдісін
жетілдіріп,дөңгелектің ауданын есептеу формуласын қорытып шығарды.Архимед
әдісінің негізгі мағынасы мынада:
• алдымен дөңгелектің ауданын оған сырттай сызылған кез келген дұрыс
көпбұрыштың ауданын кіші,бірақ оған іштей сызылған кез келген дұрыс
көпбұрыштың ауданынан үлкен екені дәлелденеді;
• одан кейін іштей және сырттай сызылған дұрыс көпбұрыштардың қабырғалар
санын шексіз екі есеге арттырғанда олардың аудандарының айырымы өте аз
шама болатын (нөлге жақындайтыны) дәлелденеді;
• ең соңында сырттай (іштей) сызылған дұрыс көпбұрыштың қабырғалар санан
шексіз екі есе арттырғанда, оның ауданының шамасы ретінде алынады.
• интеграл белгісін Г. Л е й б н и ц (1675 ж.) енгізілген . Бұл белгі «summa»
сөзіндегі S латые әріпінің өзгерген түрін елестетеді. Ал интеграл ұғымын алғаш
рет Я. Б е р н у л л и (1690 ж.) қолданды.Бұл аудармасы алғашқы күйі, қалпына
келтіру ұғымын білдіретін «integro» деген латын сөзінен шыққан. Мұның тұтас
деген мағына беретін «integer» сөзінен шығуы да мүмкін.
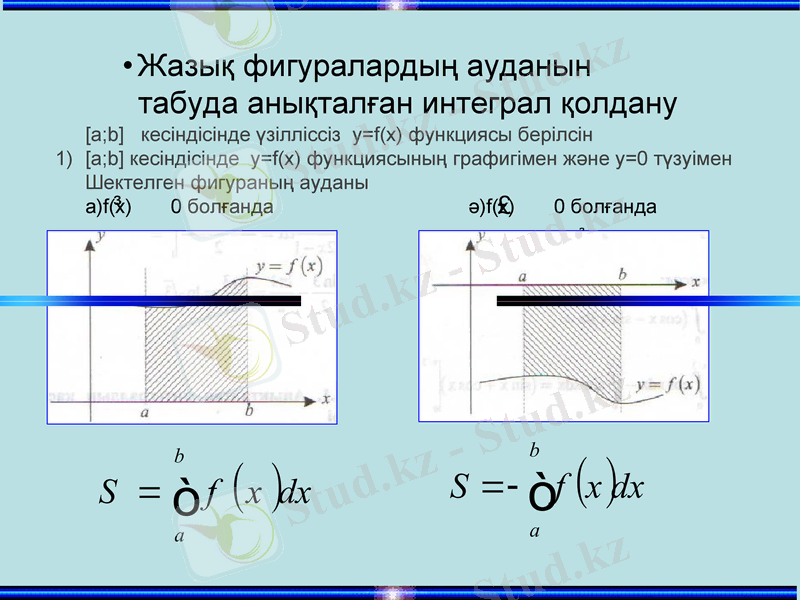
• Жазық фигуралардың ауданын табуда анықталған
интеграл қолдану
[a;b] кесіндісінде үзілліссіз у=f(х) функциясы берілсін
1) [a;b] кесіндісінде у=f(х) функциясының графигімен және у=0 түзуімен
Шектелген фигураның ауданы
а)f(х) 0 болғанда ә)f(х) 0 болғанда

b b

S f x dx S f x dx
a a
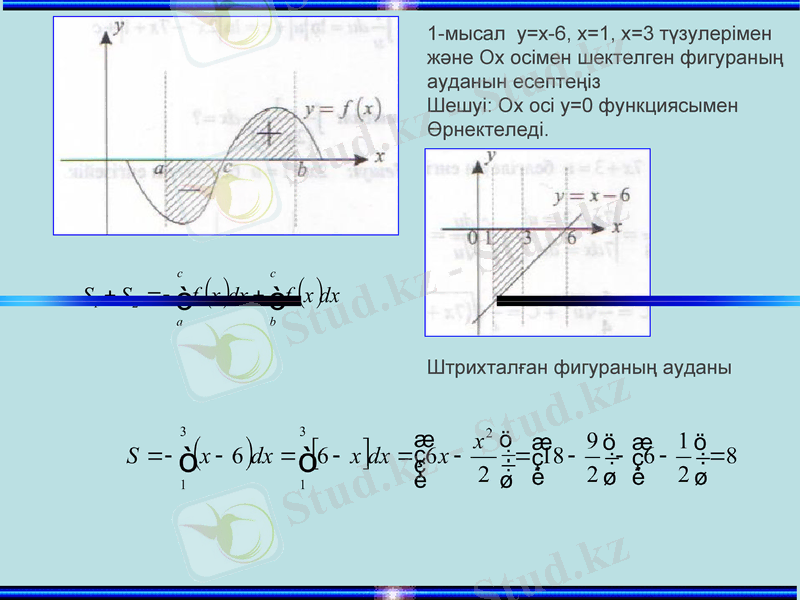
1-мысал у=х-6, х=1, х=3 түзулерімен
және Ох осімен шектелген фигураның
ауданын есептеңіз
Шешуі: Ох осі у=0 функциясымен
Өрнектеледі.

c c
S1 S 2 f x dx f x dx
a b

Штрихталған фигураның ауданы

3 3
x2 9 1
S x 6 dx 6 x dx 6 x 18 6 8
1 1 2 2 2
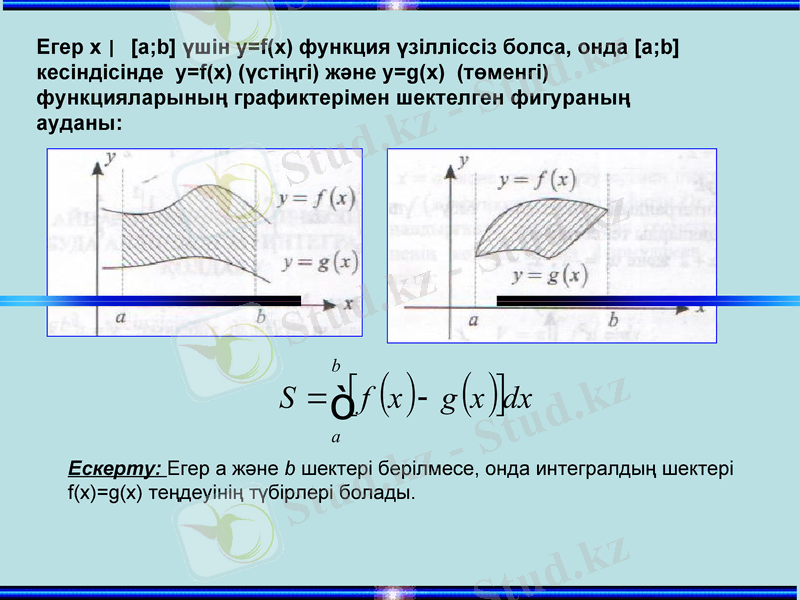
Егер х [a;b] үшін у=f(х) функция үзілліссіз болса, онда [a;b]
кесіндісінде у=f(х) (үстіңгі) және у=g(х) (төменгі)
функцияларының графиктерімен шектелген фигураның
ауданы:

b
S f x g x dx
a
Ескерту: Егер а және b шектері берілмесе, онда интегралдың шектері
f(x)=g(x) теңдеуінің түбірлері болады.
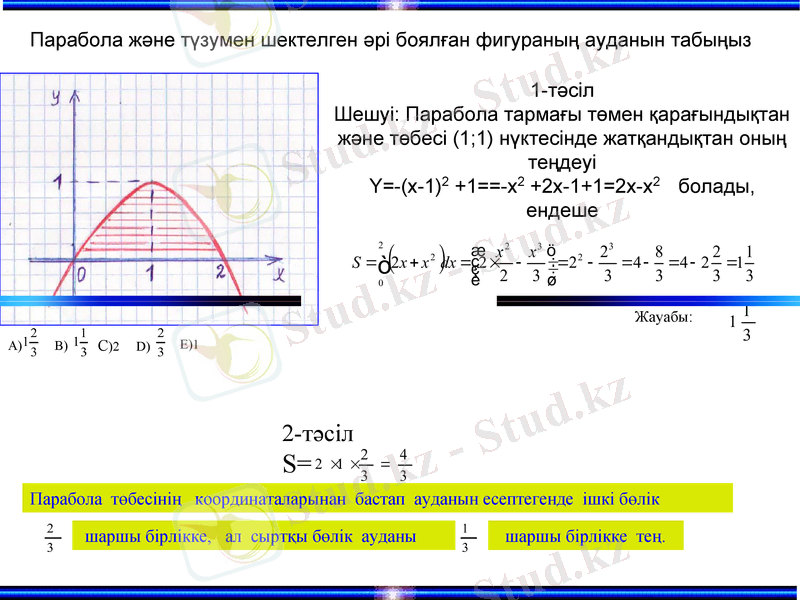
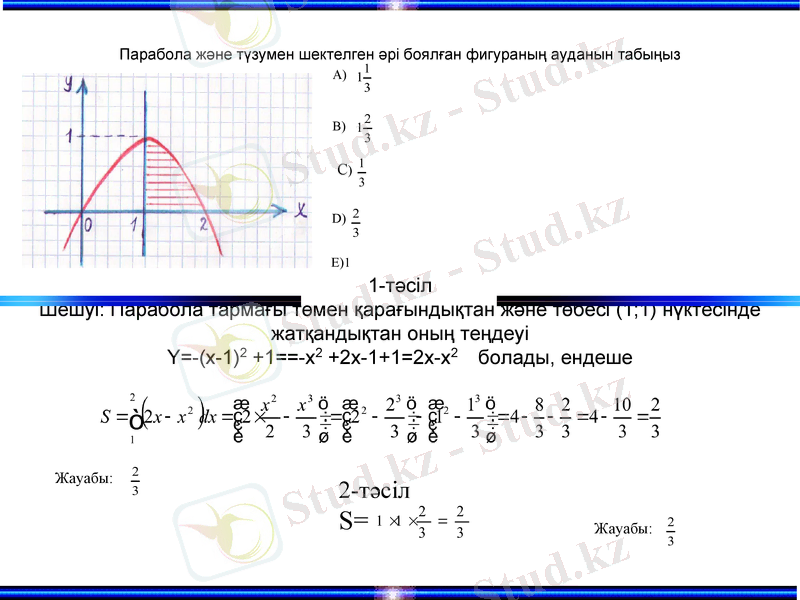
Парабола және түзумен шектелген әрі боялған фигураның ауданын табыңыз

1-тәсіл
Шешуі: Парабола тармағы төмен қарағындықтан
және төбесі (1;1) нүктесінде жатқандықтан оның
теңдеуі
Y=-(x-1)2 +1==-x2 +2х-1+1=2x-x2 болады,
ендеше
x2 x3 23 8 2 1
S 2 x x dx 2
4 4 2 1
0 2 3 3 3 3 3

Жауабы: 1
2 1 2 3
A) 1 3
B) 3 C)2 D) 3 E)1

2-тәсіл
2 4
S=2 1 3 3
Парабола төбесінің координаталарынан бастап ауданын есептегенде ішкі бөлік
2 1
шаршы бірлікке, ал сыртқы бөлік ауданы шаршы бірлікке тең.
3 3
Парабола және түзумен шектелген әрі боялған фигураның ауданын табыңыз
A) 1

В) 3

C) 1

D) 2

E)1
1-тәсіл
Шешуі: Парабола тармағы төмен қарағындықтан және төбесі (1;1) нүктесінде
жатқандықтан оның теңдеуі
Y=-(x-1)2 +1==-x2 +2х-1+1=2x-x2 болады, ендеше
x 2 x 3 2 2 3 2 13 8 2 10 2

S 2 x x dx 2
2 3
1 4 4
3 3 3 3

Жауабы:
3 2-тәсіл
2 2
S= 1 1 3 3 Жауабы: 2
Парабола және түзумен шектелген әрі боялған фигураның ауданын табыңыз

2-тәсіл S1= 13
S2=1
S3=2
1 1
S=S1+ S2+S3= 3
1 2 3

1 2 1
A 2 , B 9, C 6, D 4 , E 3
6 3 3
1-тәсіл y=4-x y=(x-1)2+1
x3 8 1 1
S1 (x 2 x 2)dx ( x 2 2 x) ( 4 4) ( 1 2) 1

1 3 3 3 3
x2
S 2 (4 x)dx (4 x ) (16 8) (8 2) 8 6 2
2 2
1 1
S=S1+S2= 1 2 3
3 3
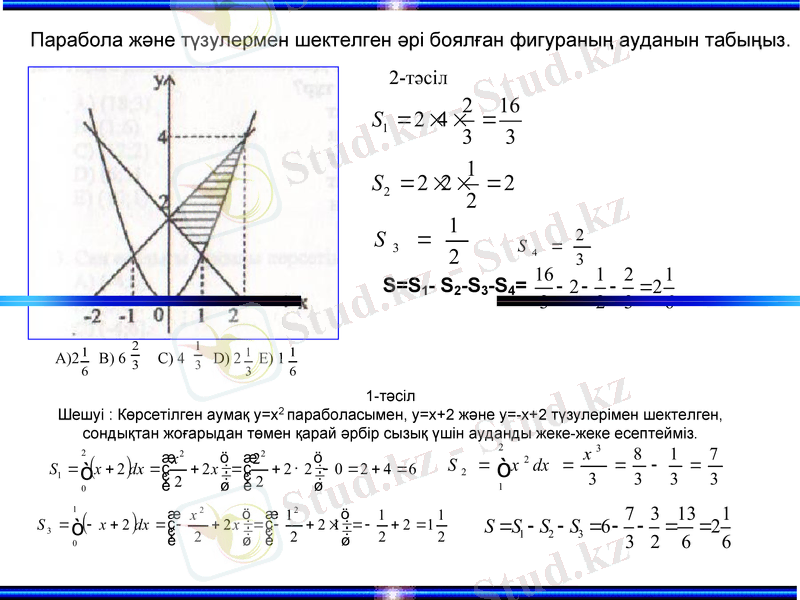
Парабола және түзулермен шектелген әрі боялған фигураның ауданын табыңыз.
2-тәсіл
2 16
S1 2 4
3 3
S 2 2 2 2
1 2
S3 S4
2 3
16 1 2 1
S=S1- S2-S3-S4= 2 2
3 2 3 6

2 1
А)2 1 В) 6 3 С) 4 3 D) 2 1 Е) 1 1
6 3 6
1-тәсіл
Шешуі : Көрсетілген аумақ у=х параболасымен, у=х+2 және у=-х+2 түзулерімен шектелген,

сондықтан жоғарыдан төмен қарай әрбір сызық үшін ауданды жеке-жеке есептейміз.
x2 22 x3 8 1 7
S1 x 2 dx 2 x 2 2 0 2 4 6 S2 x dx

0 2 2 1
3 3 3 3
x2
S 3 x 2 dx
12 1 1 7 3 13 1
2 x 2 1 2 1 S S1 S 2 S3 6 2
0 2 2 2 2 3 2 6 6
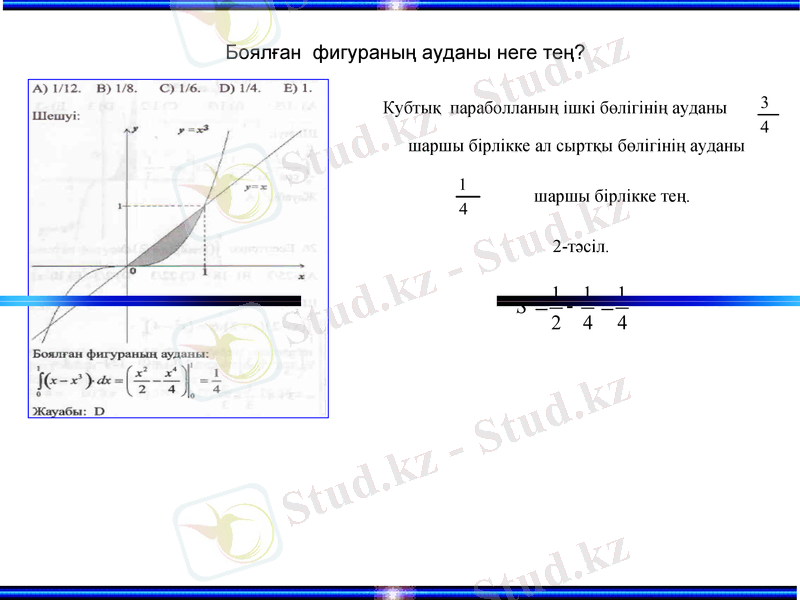
Боялған фигураның ауданы неге тең?

Кубтық параболланың ішкі бөлігінің ауданы 3
шаршы бірлікке ал сыртқы бөлігінің ауданы

шаршы бірлікке тең.

2-тәсіл.

1 1 1
S
2 4 4
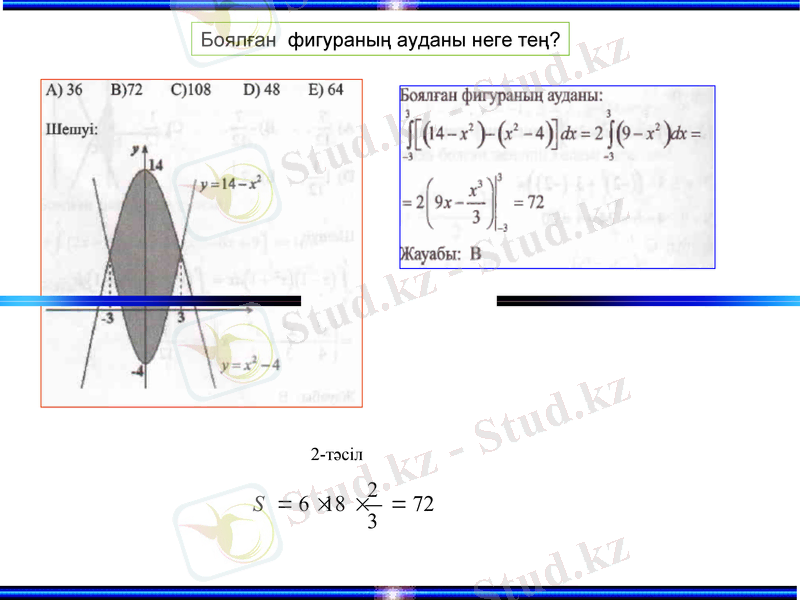
Боялған фигураның ауданы неге тең?

2-тәсіл

S 6 18 72
Параболамен және түзумен шектелген әрі боялған фигураның ауданын табыңыз
2 4
S1 1 2
3 3
2 16
S 2 2 4
3 3
20 2
S S1 S2 6
3 3

2 2 1
A) 6 B)8 D) 2 E)12 C) 9
3 3 3

Шешуі Бірінші параболаның тармағы төмен қараған және төбесі (0;5) нүктесі
болғандықтан теңдеуі у=-х2+5, ал екінші параболаның тармағы жоғары қараған, ал төбесі
(0;1) нүктесі болғандықтан теңдеуі у=(х-1)2=х2-2х+1 болады.Осы қисықтармен және у=0,
х=0, х=2 сызықтармен шектелген фигураның ауданын есептейміз.
x3 23 8 1

S 1 x 2 5 dx 5 x 5 2 10 7
0 3 3 3 3
x3 x2 23 8 2 2
S 2 x 2 2 x 1 dx 2 x 2 2 2 4 2 2 2
0 3 2 3 3 3 3
1 2 22 2 20 2
S S1 S 2 7 6
3 3 3 3 3 3
Параболамен және түзумен шектелген әрі боялған фигураның ауданын табыңыз
S1=3·5=15

1 8
S 2 2 4
3 3
S3
1 1
S4 S5
3 3
8 8 1 1 18
3 3 3 3 3

S=15-6=9
1 2
A)9 B)6 C) 9 D) 2 E)12
3 3

Шешуі Бірінші параболаның тармағы төмен қараған және төбесі (0;5) нүктесі болғандықтан теңдеуі
у=-х2+5, ал екінші параболаның тармағы жоғары қараған, ал төбесі (0;1) нүктесі болғандықтан
теңдеуі у=(х-1)2=х2-2х+1 болады.Осы қисықтармен және у=0, х=-1, х=2 сызықтармен шектелген
фигураның ауданын есептейміз.
2 2
2x3
x 5 x 2 x 1 dx 2 x 2 x 4 dx 3 2 x 4 x
2 2 2

1 1

16 2 20 7 27
4 8 1 4 9
3 3 3 3 3
VІ Қорытынды. Еліміздің үлкен тірегі болатын жас ұрпақтың терең
білімді, жан-жақты дамыған,зерек болуы заман талабы.Оқушы білімінің
қалыптасуы мұғалімнің сабақты ұйымдастыра білуіне,жаңа тақырыпты
түсіндіруінде әр түрлі әдістерді қолдана отырып жеткізуіне байланысты.
Мектеп құрылымында болып жатқан өзгерістер,білім беру мақсаттарының
алмасуы,оның дамытушылық сипаттарының бекітімді көпнұсқалы
оқытуға көшу сияқты мәселері мұғалімдерден шығармашылықты және
бөлек көзқарастарды,жұмыстың жоғары сапасын және кәсібилікті талап
етеді.
«Халықты халықпен,адамды адаммен теңестіретін-білім»-деп М.Әуезов атап
көрсеткеніндей,еліміздің келешегі кемел білім мен ұлағатты тәрбиеге
байланысты.

Ұқсас жұмыстар

Шаймерденовна Мадетқызы жоғары санатты математика жоғары санатты математика пәнінің мұғалімі пәнінің мұғалімі

Құйрық бауыр асатудың мағынасы

Логарифм және оның қасиеттері. Excel көмегімен есептер шығару

Үздік кіріктірілген сабақ байқауы – 2010”

Бағдарламалау тілінде белгілеуі

Математика сабағында оқушыларды ұлттық рухта адамгершілікке тәрбиелеу

Ақиқаттық кестелері. Компьютердің логикалық негіздері. 8 сынып

Қазақтың тұнғыш географы

Теңсіздіктер жүйесінің шешімін тап

МОӘ курсы болашақ математика мұғалімінің әдістемелік құзырлылығын қалыптастырудың негізгі құралы

Пәндер