Декарттық координаталық жазықтық: анықтамасы, координаталарды анықтау және практикалық тапсырмалар

Координаталық жазықтықта координаталары берілген нүктелерді сала білуге,

координаталық жазықтықта берілген нүктелердің координаталарын таба білуге үйрету;

Тақырыпты үш топтың сайысы арқылы олардың қызығушылығын арттыра отырып, оқушылрдың санасына теренірек қалыптастыру;

Оқушылардың математикалық мәдениеттілігін салауаттылығын есептер шығару барысында қалыптастыру;

№ 1153, 1157

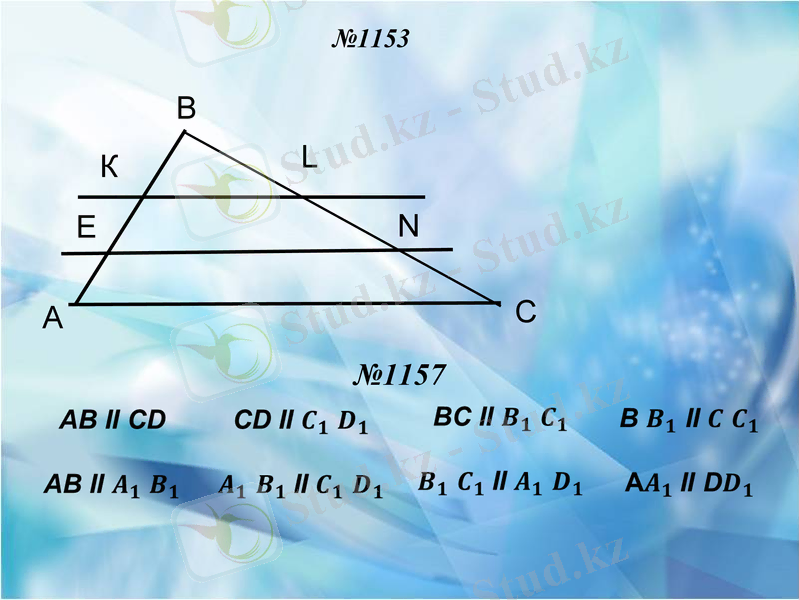
№1153

№1157

Сонда координаталар жүйесі - санақ басы ортақ, өзара перпендикуляр екі координаталық түзу. Сондықтан мұны тікбұрышты координаталар жүйесі деп атайды.

Тік бұрышты координаталар жүйесі француз философы және математигі Рене Декарттың (1596-1650) құрметіне декарттық координаталар жүйесі деп те аталады.

Тік бұрышты координаталар жүйесі орналасқан жазықтық координаталық жазықтық деп аталады. «Координаталар» сөзі латынның - қазақша «реттелген» деген сөзінен алынған. Координаталық түзулер координаталық осьтер деп аталады. Горизонталь сызылған координаталық түзу абсциссалары (Ох) осі деп аталады да, солдан оңға қарай бағытталады. Вертикаль сызылған координаталық түзу ординаталар (Оу) осі деп аталады да, төменнен жоғары қарай бағытталады.

Абсциссалар осі мен ординаталар осінің қиылысуы нүктесін координаталар басы деп атайды. Координаталар басы О әрпімен белгіленеді.

Берілген нүктенің абсциссасы мен ординатасы нүктенің координаталары деп аталады.

Координаталық жазықтықтағы А нүктесінің координаталарын табу үшін

1. А нүктесінен абсциссалар осіне перпендикуляр түсіріп, оның Ох осімен қиылысу нүктесінің координатасын табу керек. Сол А нүктесінің абсциссасы болады;

2. А нүктесінен ординаталар осіне перпендикуляр түсіріп, оның Оу осімен қиылысу нүктесінің координатасын табу керек. Сол Анүктесінің ординатасы болады.

«А нүктесінің координаталары 4 пен 3». Нүктенің жазықтағы орны сандар жұбымен анықталады. Нүктенің координаталарын жазғанда абциссасы бірінші орынға, ординатасы екінші орынға жазылады.

х осіндегі кез келген нүктенің ординатасы 0-ге тең (х; 0) .

Мысалы, Е(-3; 0) ; Ғ(4; 0)

у осіндегі кез келген нүктенің абсциссасы 0-ге тең: (0; у) . Мысалы, К(0; 2) ; (0; -4)

Координаталары бойынша нүктені салу.

Мысалы, координаталық жазықтықта (-3; 4) нүктесін салайық.

Ол үшін:

1. х=-3; у=0 нүктеден абсциссалар осіне перпендикуляр жүргіземіз.

2. х=0; у=4 нүктеден ординаталар осіне перпендикуляр жүргіземіз.

3. Осы түзулердің қиылысу нүктесі (-3; 4) нүктесі болады.

Координаталар осьтері жазықтықты төрт бөлікке бөледі. Оларды ширектер деп атайды.

Ширектердің рет саны сағат тілінің қозғалыс бағытына қарсы бағытта анықталады

(-; +)

(+; +)

(-; -)

(+; -)

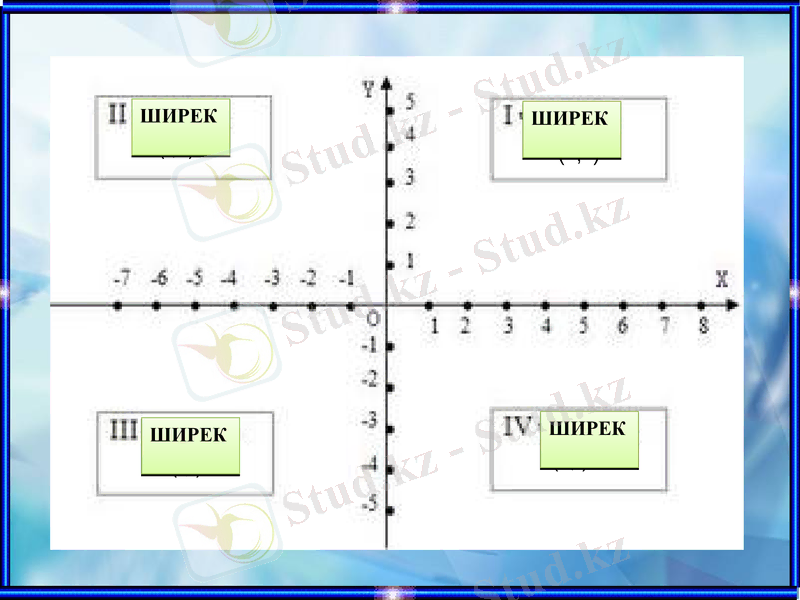
ШИРЕК

Практикалық жұмыс

№1 Координаталық жазықтықта нүктелерді салып, сурет құрастыр.

(0; 1), (4; 1), (6; 2), (8; 0), (8; -4), (5; -6), (4; -4), (4; -8), (3; -9), (2; -9),

(0; -9), (0; -8), (2; -8), (3; -7), (1; -5), (0; -5), (-1; -4), (-2; -6), (-5; -4), (-6; -1), (-2; 2),

(-10; -2), (-13; -4), (-14; -7), (-16; -9), (-13; -7), (-12; -10),

(-13; -14), (-10; -14), (-9; -13), (-10; -9), (-5; -9),

(-5; -15), (-2; -15), (-2; -10), (-1; -10), (-1; -11), (-2; -13), (0; -15), (2; -11) .

Көзі: (0; -2), (4; -2) .

№2

1) (3; - 4), (3; - 1), (2; 3), (2; 5), (3; 6), (3; 8), (2; 9), (1; 9), (- 1; 7), (- 1; 6),

(- 4; 4), (- 2; 3), (- 1; 3), (- 1; 1), (- 2; 1), (-2; - 1), (- 1; 0), (- 1; - 4), (- 2; - 4), (- 2; - 6), (- 3; - 6), (- 3; - 7), (- 1; - 7), (- 1; - 5), (1; - 5), (1; - 6), (3; - 6), (3; - 7), (4; - 7), (4; - 5), (2; - 5), (3; - 4) .

2) құйрығы: (3; - 3), (5; - 3), (5; 3) .

3) көзі: (- 1; 5) .

№3

1) (- 3; 0), (- 2; 1), (3; 1), (3; 2), (5; 5), (5; 3), (6; 2), (7; 2), (7; 1, 5), (5; 0), (4; 0), (4; - 1, 5), (3; - 1), (3; - 1, 5), (4; - 2, 5), (4, 5; - 2, 5), (- 4, 5; - 3), (3, 5; - 3), (2; - 1, 5), (2; - 1), (- 2; - 2), (- 2; - 2, 5), (- 1; - 2, 5), (- 1; - 3), (- 3; - 3), (- 3; - 2), (- 2; - 1), (- 3; - 1), (- 4; - 2), (- 7; - 2), (- 8; - 1), (- 7; 0), (- 3; 0) .

2) көзі: (5; 2) .