Директрисалардың тендеу

Презентация қосу

Екінші peтті қисықтар
жене олардың канондық
теңдеулері
Орындаған: Агибаев Арман
Анықтама:
Жоғары математкада екінші
дәрежелі теңдеулермен анықталатын
сызықтарды екші pеттi қисықтар
деп атайды. Олар негізінен шеңбер,
эллипс, гипербола және парабола деп
аталады. Бұл қисықтар техника мен
ғылым саласында жиі кездеседі.
1. Шеңбер.
Шеңбердеп аталатын берілген нүктеден бірдей қашықтықта жататын
жазықтықтағы нүктелердің геометриялық орындарын шенбер деп атайды .
С(х0,у0) -берілген нукте. Шеңбердің бойынан кез келген

жылжымалы М(х,у) нүктесін алайык. Сонда СМ(х -х0,у-у0),

мұндағы F1 және F2 -фокус деп аталатын берілген центрі С нуктесінде
жаткан радиусы R -ге тең шеңбердің канондық теңдеуі.
Егер шеңбердің центрі С координаттардың бас нүктесінде
жатса, онда х0 = у0 = 0 .Сондыктан : х2 +у2 = R2
2. Элипс.
Фокустар деп аталатын берілген екі нүктеден
қашықтықтарыньң қосындысы әрқашанда тұрақты шама
болатын жазықтықтағы нұктелердің геометриялык
орындарын эллипс деп атайды . Анықтама бойынша F1M
+ F2M = 2a
нүктелер,

М{х, у) -эллипстің бойындағы кез келген жылжымалы
нүкте, 2а-тұрақты шама.
Егер F1F2 = 2с десек, онда F1(-C;0), F2(C;0). Сонда:

Енді осы мәндерді қойсақ:

Немесе
Анықтама.
Егер а>с болса, онда а2 —с2=b2 болады. Сондықтан эллипстің
канондық теңдеуі деп аталатын теңдеуге келеміз:

Мұндағы х пен у эллипстің кез келген жылжымалы нүктесінің координаттары, а
-эллипстің үлкен жарты oci, b -онын кіші жарты oci.
Осьтер эллипске симметриялы, ал симметриялы осьтердің қиылысатын
нуктесі эллипстің цeнтpi болады.
қатынасын эллипстің эсцентриситеті деп атайды және оны деп

белгілейді. Сонымен 6ipгe а > с болғандьқтан l < 1 немесе
Эллипстің үлкен осіне перпендикуляр тузулердің ішінде 6ip түзудің эллипстің кіші
осінен қашықтықты d әрқашанда а/l қатынасына тең тұрақты шама болса,
онда мұндай тузуді эллипстің директрисасы деп атайды. Директрисалардың
тендеу . Эллипс үшін l < 1 болғандьқтан .

Сондықтан эллипстің дериктрисалары оның сыртында жатады.
Егер a=b болса, онда шеңбер эллипстің дерпбес жағдайы болады. Бұл
жағдайда с=0, ендеше шеңбердің эксцентриситеті нөлге тең.
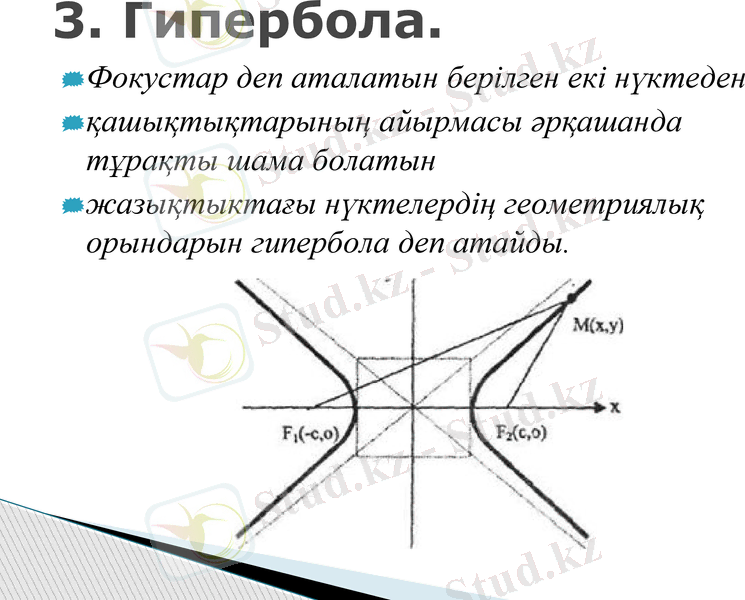
3. Гипербола.
Фокустар деп аталатын берілген екі нүктеден
қашықтықтарының айырмасы әрқашанда

тұрақты шама болатын
жазықтыктағы нүктелердің геометриялық

орындарын гипербола деп атайды.
4. Парабола.
Фокус деп аталатын берілген нүктеден және
директриса деп аталатын берілген түзуден ара
қашықтықтары бірдей болатын жазықтықтарды
нүктелерің геометриялык орындарын парабола
дейді Берілген F нуктесінің координаталарын
былай белгілейді
Анықтама.
Координаталардың бас нүктесінен Р/2 қашықтықтағы ординат осіне параллель
берілген тузуді параболаның директрисасы дейді.
М(х,у) - параболаның бойындағы кез келген жылжымалы нүкте.
Анықтама бойынша
FM=ME
Екі нүктенің ара қашықтыгыньң формуласы бойынша

осы мәндерді апарып қойып, шыққан өрнекті түрлендірсек,
параболаның канондық теңдеуі шығады:
у2=2рх
мұндагы р -берілген фокус пен директрисаның арасындағы
қашықтық, х пен у - параболаның бойындағы кез келген жылжымалы
нуктенің координатасы.
Параболаның эксцентриситеті:

Параболаның директрисасының теңдеуі:
Назарларыңызға рахмет

Ұқсас жұмыстар

Сабақтың мақсаттары

Оқушылардың ойлау және есте сақтау қабілетін дамыту

Квадрат теңдеудің түрлері

Толық квадрат Келтірілген квадрат

Теңдеулер мен теңдеулер жүйелерін шешу тақырыбына қайталау

Теңдеудің түбірін табыңдар

Квадрат теңдеулер

Квадрат теңдеу түбірлерінің формулалары

Квадрат үшмүшені көбейткіштерге жіктеуңдер

Теңдеулер құруға берıлген есептердı шығару әдıстемесı

Пәндер