Инверсия және шеңберлер

Презентация қосу

Тақырыбы
Инверсия және оның қолданылуы

Орындаған
04401 топ студенті Қ.Т. Досқайырова
Ғылыми жетекші
Аға оқытушы Ж.С. Камкиева
Мазмұны
Кіріспе
1. Инверсия және шеңберлер .шоғы
1.1 Жазықтықтың қарапайым түрлендірілулері
1.2 Стереографиялық проекция. Жазықтықтың шексіз алыстағы
нүктесі
1.3 Инверсия
1.4 Инверсия қасиеттері
1.5 Шеңберге қатысты нүктенің дәрежесі. Екі шеңбердің
радикалдық осі
1.6 Инверсияны салу есептерін шешуде қолдану
1.7 Шеңберлер шоғы
1.8 Эллипстік шоқтың құрылымы
1.9 Параболалық шоқтың құрылымы
1.10 Гиперболалық шоқтың құрылымы
1.11 Птолемей теоремасы
2. Комплекс сандар және инверсия
2.1 Комплекс сандардың геометриялық кескіні және оларға
қолданылатын амалдар
2.2 Комплекс айнымалының сызықтық функциясы және
жазықтықтың қарапайым түрлендірілулері
2.3 Комплекс айнымалының бөлшек-сызықтық функциясы және
жазықтықтың нүктелік түрлендірілулері
Қорытынды

Тақырыптың өзектілігі: Геометрия есептерін
шешудің бірнеше әдісі бар. Солардың бірі-түрлендірулер әдісі.
Планиметрия есептерін алгебралық әдіспен шешуге қарағанда
түрлендірулерді қолданып шешу әлде қайда қысқа болып
табылады. Оқушыларға бір есепті бірнеше әдіспен шешіп
көрсету олардың математикаға қызығушылығын арттырады,
ойлау қабілетін дамытады. Геометриялық есепті түрлендірулер
әдісімен шешу оңай болмайды. Берілген есеп үшін қандай
түрлендіру пайдаланатынын тағайындап алу керек. Ал есепті
инверсияны пайдаланып шешу шағын шығармышылық
жұмыс. Сондықтан бұл түрлендіруге қатысты теориялық
білімдерді математика мұғалімінің жете білуі міндетті.
Мақсаты: Инверсия түрлендіруіне және оның
қолданылуына қатысты білімдер жүйесін
жасақтау
Міндеттері:
- Инверсия түрлендіруі туралы теориялық
материалдар жинақтау;
- Инверсияның комплекс айнымалының
бөлшек-сызықтық функциямен байланысын
көрсету;
- Инверсия түрлендіруін салу есептерін шешуге
қолдануды көрсету;
- Осы тақырып бойынша тест сұрақтарын
құрастыру
Жазықтықтың қарапайым
түрлендірулері

Біз жазықтықтың әртүрлі түрлендірулерін
білеміз. Олар: өстік симметрия, паралель
көшіру, бұру т.б.

Дәл қазір түрлендірудің басқа бір класы –
шеңберге қатысты инверсияны қарастырамыз.
Инверсия анықтамасы
Инверсияның қарапайым қасиеттері
1. Егер нүктесі нүктесіне инверсиялы болса, онда, керісінше,
нүктесі нүктесіне инверсиялы болады.
2. Егер инверсияда фигурасы фигурасына түрленсе, онда
фигурасы фигурасына түрленеді.
3. Жазықтықтың ешбір нүктесі инверсия центріне инверсиялы
болмайды.
4. Базистік шеңбердің әрбір нүктесі өз-өзіне инверсиялы болады.
5. Егер берілген нүкте базистік шеңбердің сыртында жатса, онда
оған инверсиялы нүкте оның ішінде жатады және керісінше.
6. Базистік шеңбердің сыртындағы нүкте одан шексіз алыстаған
сайын, оған инверсиялы нүкте инверсия центріне шексіз
жақындайды. Керісінше сөйлем дұрыс болады.
7. Инверсия центрінен шығатын сәуле инверсияда өз-өзіне
түрленеді (көшеді) және де базистік шеңберге қатысты сәуленің
ішкі нүктелері оның сыртқы нүктелеріне көшеді және керісінше.
8. Инверсия центрі арқылы өтетін түзу өз-өзіне көшеді.
мысалдар

Салу есептерін инверсия әдісімен шешкенде қолданылатын
теоремалар:
Теорема1: Инверсия центрі арқылы өтетін шеңбер инверсияда түзуге
көшеді және бұл түзу инверсия центрі арқылы өтетін түзуге
перпендикуляр болады.
Теорема2:Инверсия центрі арқылы өтпейтін шеңбер инверсияда
шеңберге көшеді.
Теорема3: Инверсия центрі арқылы өтпейтін түзу инверсияда шеңберге
ккөшеді және ол шеңбер инверсия центрі арқылы өтеді.
Теорема4: егер шеңбер өзара инверсиялы екі шеңбер арқылы өтсе, онда
инверсияда ол шеңбер өзіне көшеді.
Теорема5: Егер сызықтары бір-бірінен инверсия центрінен өзге
нүктесінде жанасса, онда олардың образдары нүктесінде жанасады.
Мұнда шеңбер немесе түзу, ал шеңбер.
Теорема6:Базистік шеңберден өзге шеңбер инверсияда өз-өзіне көшу
үшін, оның базис шеңберге ортогональ болуы қажет және жеткілікті.
Шеңберлер шоғы
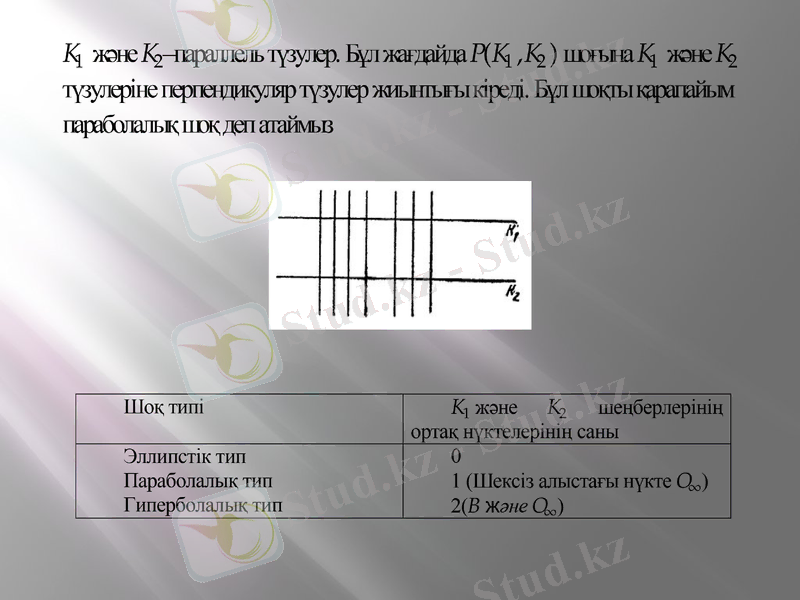
Кез келген шоқтың нөлдік және тораптық
нүктелерінің ортақ саны екіге тең.
Гиперболалық шоқ нөлдік нүктелерінің немесе нөлдік
нүктесінің есебіне және радикалдық осіне байланысты
толық анықталады
Комплекс сандар және инверсия
Комплекс айнымалының сызықтық функциясы
және жазықтықтың қарапайым түрлендірілулері
Комплекс айнымалының бөлшек-сызықтық функциясы
және жазықтықтың нүктелік түрлендірілулері
Назарларыңызға
рахмет!!!

Ұқсас жұмыстар

Негізгі логикалық элементтер

Коммутациялық станцияның құрылымдық сұлбасы

Инвертті шырын қосылған карамель сапалық көрсеткішін анықтау

Мутацияның заманауи жіктелуі

НГО әдісі

Абразивті құралдармен өңдеу

ЕМЕС схемасының ақиқаттық кестесі ЕМЕС схемасы

Аймақтық температура мәндерін биіктігі бойынша бөлу

Мағжан Жұмабаев өлең өрнегіндегі буын мен бунақ ерекшеліктері

Геномдық, хромосомалық және гендік мутациялардың жіктелуі

Пәндер