№24 Экономика және бизнес арнаулы лицейінің квадрат теңдеулерге арналған ашық сабақ жоспары

Ашық сабақ Тақырыбы: Квадрат теңдеулер

Дарынды балаларға арналған үш тілде оқытатын Мұхтар Арын атындағы

№24 «Экономика және бизнес» арнаулы лицейі

Тулеметова Камида Әбілдабекқызы.

2014 жыл

Мақсаты

Күтілетін нәтиже:

- есеп шығарғанда формуланы пайдаланып, оқушылар квадрат теңдеуді шеше алады;

- квадрат теңдеулердің дербес жағдайларын шешуді біледі;

- квадрат теңдеудің формуласын және Виет теоремасын есеп шығаруда дұрыс пайдалана алады;

- ойларын нақты жеткізе алады;

- жаңа айнымалы енгізу әдісімен күрделі деңгейдегі шығармашылық есептерді шығарады және талдай алады;

өз білімдерін сынайды, сыни тұрғыдан ойлай алады, қызығушылығы артады;

Әдіс - тәсілдер: Диалогтық оқыту, миға шабуыл, жұптық әдіс

Сабақтың түрі: аралас сабақ

Сабақтың көрнекілігі: интербелсенді тақта,

слайд, үйлестірмелі

карточкалар, бағалау парағы

Өзіңе сен өзіңнің күшіңе сен,

Алып шығар білімің мен

еңбегің екі жақтап.

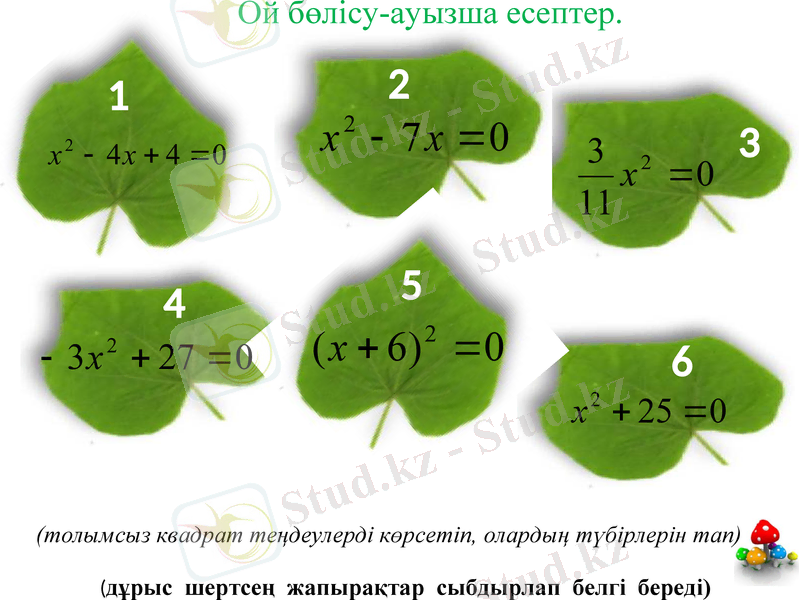
(дұрыс шертсең жапырақтар сыбдырлап белгі береді)

(толымсыз квадрат теңдеулерді көрсетіп, олардың түбірлерін тап)

Ой бөлісу-ауызша есептер.

Ой толғау - деңгейлік тапсырма

Теңдеуді шешіңдер:

А) Б) В)

(дұрысы тышқанмен шерткенде жасыл түске боялады)

теңдеуі түбірлерінің айырымы 2-ге тең болса,

-ды табыңдар.

Кім тапқыр

Жаңа айнымалыны енгізу әдісін қолданып, теңдеуді шеш

Екі санның арифметикалық ортасы 7-ге, ал квадраттарының айырымы 56-ға тең. Осы екі санның квадраттарының қосындысын тап.

(дұрыс тапсаң шар әуеге қалықтайды!)

Сергіту сәті

Ой сергіту - шығармашылық тапсырма.

Симметриялы теңдеуді шеш:

Тест жауабы

№1. С

№2. В

№3. Д

№4. С

№5. Д

№6. С

5. ах2=0, ax2+c=0, ax2+bx=0

квадрат теңдеу деп аталады

Квадрат теңдеу түбірлерінің формуласы

Келтірілген квадрат теңдеу

Виет теоремасы

Қорытынды

Толымсыз квадрат теңдеу

Үйге тапсырма

№485, №488, №493

VІ. Ой түйін - тест тапсырма.

№1. Теңдеуді шешіңдер. x²+14x+13=0

А) 1; 14 В) -1; 13 С) -1; -13 Д) Түбірі жоқ

№2. Теңдеуді шеш. 2x²-x+3=0

А) 1; -3 В) Түбірі жоқ С) 3; -1 Д) 2; 3

№3. Түбірлері 1-ге және -3 - ке тең квадрат теңдеу құрыңдар.

А) х2 +3х-1=0 В) x2 -3x+1=0 С) x2 -x-3=0 Д) x2+2x-3=0

№4. m-нің қандай мәнінде x2-3x+m=0 теңдеуінің бір түбірі 2-ге тең?

А) 4 В) 3 С) 2 Д) 1

№5. Теңдеуді шеш:

А) 0; -3 В) 0; 4 С) Д)

№6. Түбірлерінің қосындысын табыңдар: 4x²-11x=0

А) 11 В) 5, 5 С) 2, 75 Д) 2, 5

Ұқсас жұмыстар

Квадрат теңдеулерді шешу тәсілдері: ашық сабақ жоспары

Ашық сабақ: 26+24 пен 50-24 жағдайларындағы қосу мен азайту

Ашық сабақ: Квадрат үшмүшені көбейткіштерге жіктеу

Алматыда 150 автокөлікке арналған ашық аспан астындағы автокинотеатрдың бизнес-жоспары

Ашық сабақ: Бір айнымалысы бар квадрат теңсіздіктерді аралықтар тәсілімен шешу

Әбділда Тәжібаевтың Сырдария өлеңін талдауға арналған ашық сабақ жоспары

Жай бөлшектерді азайту: 5-сыныпқа арналған ашық сабақ жоспары

Үйкеліс күші: 7-сыныпқа арналған ашық сабақ жоспары

Квадрат теңдеулер: сабақ жоспары және жаттығу тапсырмалары

Квадрат түбірлер тарауын қайталау: сабақ жоспары мен тапсырмалар

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz