Көрсеткіштік теңдеулер және оларды шешу әдістері



Қош келдіңіздер!

Ашық сабақ
Тақырыбы: «Көрсеткіштік теңдеулер және оларды шешу тәсілдері»
Оқу тобы: РС - 15о
Оқытушы: Айтбаева Н.

Мақсаты: Оқушыларға көрсеткіштік теңдеулерге анықтама беру және оларды шешудің тәсілдерін үйрету. Теңдеулердің қарапайым және күрделі түрлерін оқушыларға шығарып үйрету және алған білімдерін тереңдету.
Білімділігі: Әрбір оқушыға сапалы да терең білім беру, ой өрісін кеңейту. Интерактивті тақта мүмкіндіктерін пайдаланып алған білімдерін жаңарту. Оқушыларға көрсеткіштік теңдеулер мен олардың шешу тәсілдеріне әртүрлі мысалдар келтіріп, тақырыпты санасына бекіту.
Дамытушылығы: Жеке тұлғаның ойлау қабілеті мен есте сақтау қабілеттерін жетілдіріп, шығармашылық ізденісін дамыту.
Тәрбиелігі: Меңгерген білімнің өмірге қажеттілігін түсіндіру. Оқушыларды ұқыптылыққа, шапшаңдыққа, еңбексүйгіштікке, логикалық ойлауға, жүйелі жұмыс істеуге, өзінше еңбек етуге, өз-өзін бағала, білімін тиянақтай білуге тәрбиелеу.
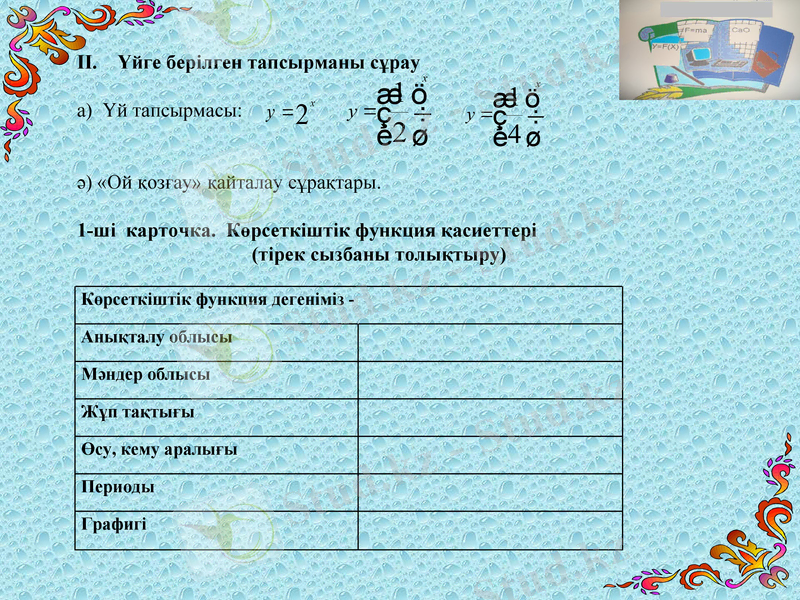
Көрсеткіштік функция дегеніміз -
Анықталу облысы
Мәндер облысы
Жұп тақтығы
Өсу, кему аралығы
Периоды
Графигі
ІІ. Үйге берілген тапсырманы сұрау
а) Үй тапсырмасы:
ә) «Ой қозғау» қайталау сұрақтары.
1-ші карточка. Көрсеткіштік функция қасиеттері
(тірек сызбаны толықтыру)

Логарифм дегеніміз -
logaa=
loga1=
loga(x∙y) =
loga(x/y) =
logaxk=
Ондық логарифм -
2 карточка. Логарифмнің қасиеттері

Арифметикалық түбір дегеніміз -
=
=
=
=
=
3 карточка. Нақты көрсеткішті дәреже қасиеттері

ІІІ. Жаңа сабақ
Құрамына әріп енетін және онымен белгіленетін санды іздеу мақсатында қойылған теңдікті қалай атайды? (Жауабы теңдеу) Оқушылар қойылған сұраққа жауап бергеннен кейін жаңа сабақтын тақырыбы және қаралатын сұрақтар аталады.
Тақырыбы: «Көрсеткіштік теңдеулер және оларды шешу тәсілдері»
1. Қарапайым көрсеткіштік теңдеулер
2. Бірдей негізге келтіру тәсілі
3. Жаңа айнымалы енгізу тәсілі
Анықтама: Айнымалысы дәреже көрсеткішінде болатын теңдеуді көрсеткіштік теңдеу деп атайды.
Мысалы:
,
,
,
Көрсеткіштік теңдеудің қарапайым түрі : aх = b
Мұндағы a > 0, a ≠ 1 және b < 0 немесе b=0, болғанда теңдеудің түбірі болмайды.

Көрсеткіштік теңдеу екі тәсілмен шығарылады:
І . Теңдеуді бірдей негізге келтіру
ІІ . Теңдеуге жаңа айнымалы енгізу тәсілі

Бірдей негізге келтіру тәсілімен көрсеткіштік теңдеулерді шығару үшін мынадай алгортмдер қолданылады.
Теңдеудің екі жағын бірдей негізге келтіреміз
Теңдеу бірдей негізге келтірілгеннен кейін олардың сол және оң жақ бөлігіндегі дәреже көрсеткіштерін теңестіріп, алгебралық теңдеу аламыз
Осы алгебралық теңдеуді шешеміз
Табылған түбірлерді берілген теңдеудегі айнымалының орнына апарып қойып тексереміз.
Тексеру нәтижесіне қарап берілген теңдеудің жауабын жазамыз
1-мысал.
8х= 64 теңдеуді шешейік. Тексеру:
23x= 26 82 = 64
3x = 6 64=64
х = 2 жауабы : 2
2-мысал.
5х =125 теңдеуді шешейік. Тексеру:
5х =53 53 =125
х = 3 125=125
жауабы : 3

Жаңа айнымалы енгізу тәсілі
Көрсеткіштік теңдеулерді жаңа айнымалы енгізу тәсілімен шығарғанда, төмендегідей алгоритм қолданылады.
Айнымалыларды жаңа айнымалымен ауыстырып алгебралық теңдеу аламыз
Осы алгебралық теңдеуді шешеміз
Алгебралық теңдеудің табылған түбірлерін алмастырылған теңдікке қойып, алғашқы айнымалының мәндерін анықтаймыз.
Табылған мәндерді берілген теңдеудегі айнымалының орнына қойып тексереміз.
Берілген теңдеудің жауабын жазамыз
3-мысал.
32х+5= 3x+2 + 2 теңдеуді шешейік
3x= y деп жаңа айнымалы енгізіп, берілген теңдіктен мынадай квадрат теңдеу аламыз.
243у2-9у-2=0
Бұл квадрат теңдеудің түбірлері мынаған тең.
теріс, ал 3x< 0 болуы мүмкін емес, сондықтан алмастыру шарты бойынша түбірін аламыз. Табылған мәнін
3x=y теңдігіне қоямыз: х=-2
Жауабы : -2

ІV. Мағынаны тану.
Ментальды карта.
Шығарылған тапсырманы түсіндіріп қорғау.
1-топ 2-топ
27х = 22х+3∙2х-4=0
3-топ
52х-6∙5х+5=0

V. Сабақты бекіту. Оқулықпен жұмыс. Деңгейлік тапсырмалар Сәйкестік тест.
А деңгей
1) 8x=16 2)
В деңгей
1) 2x+2x+1=12 2) 3x+3x+1+3x+2=117
С деңгей
1) 25х - 26·5х + 25 = 0 2) 2·22х-3·2х-2=0
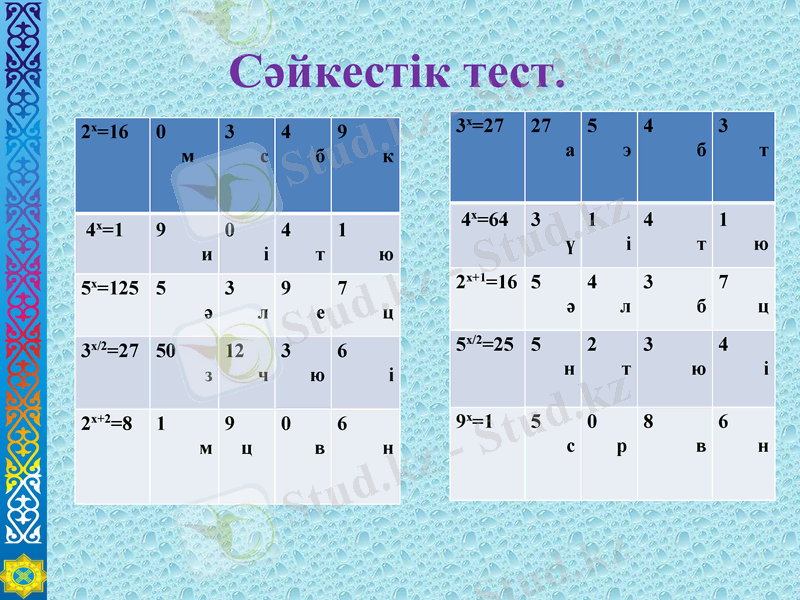
Сәйкестік тест.
2х=16
0
м
3
с
4
б
9
к
4х=1
9
и
0
і
4
т
1
ю
5х=125
5
ә
3
л
9
е
7
ц
3х/2=27
50
з
12
ч
3
ю
6
і
2х+2=8
1
м
9
ц
0
в
6
н
3х=27
27
а
5
э
4
б
3
т
4х=64
3
ү
1
і
4
т
1
ю
2х+1=16
5
ә
4
л
3
б
7
ц
5х/2=25
5
н
2
т
3
ю
4
і
9х=1
5
с
0
р
8
в
6
н

Сәйкестік тест
5х=1
27
а
5
э
0
ғ
3
т
2х=8
3
ы
1
і
4
т
1
ю
9х/2=9
5
ә
2
л
3
б
7
ц
3х/2=27
5
н
2
т
3
ю
6
ы
6х+2=216
5
с
1
м
8
в
6
н

Логикалық сұрақтар
Қандай сандар нольден үлкен?
Оң сандар
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz