Осьтік және центрлік симметрия

Презентация қосу

АЛТЫН ЕРЕЖЕ
Мақсатшыл болу
Белсенді болу
Бірлесіп жұмыс атқару
Ынтымақтастықта болу
Тыңдай білу
Әділ болу
Уақытты тиімді
пайдалану
Сабақтың тақырыбы:

Осьтік және
центрлік
симметрия
Сабақтың
мақсаты:
Симметрия туралы түсінік бере
отырып, түзуге қатысты
фигураларды, центрлік
симметриялы фигураларды,
осьтік симметриялы
фигураларды және де
симметриялы фигуралардың
өзара теңдігін үйрену.
Оқыту
нәтижесі:
Өздігінен оқу дағдыларын
қалыптастырады. Жаңа
тақырыптың мазмұнын өз
бетімен аша алады,
салыстыра біледі, талдай
алады, ой қорытуды
үйренеді.
Түйінді
идеялар:
1) Интернеттен мәлімет іздеу
оқушылардың тәуелсіз ойлауына және
олардың ой қорыту, өзіндік түсініктеме
беру қабілетіне ықпалын тигізеді.
2) Сыни тұрғыдан ойлау балалардың
өз идеясын сенімді түрде білдіруіне,
түрлі көзқарастарға көңіл бөлуге және
оларды бағалауға мүмкіндік береді.
3) Балалардың жауабын бақылау, жазып
алу мен талқылау сауатты оқытуға
ықпал етеді.
ТЕСТ
I НҰСҚА
1. (-∞; 5] САН АРАЛЫҒЫНЫҢ АТЫ:
А) АШЫҚ СӘУЛЕ, Ә) ИНТЕРВАЛ, Б) КЕСІНДІ,
В) СӘУЛЕ
2. БЕЛГІЛЕНУІМЕН ЖАЗ: 1-ДЕН 4-КЕ ДЕЙІНГІ
КЕСІНДІ
А) (1; 4 ), Ә) [1; 4], Б) ( 1; 4 ], В) [ 1; 4)
3. А-НЫҢ ҚАНДАЙ МӘНДЕРІНДЕ
БӨЛШЕГІ БҰРЫС БӨЛШЕК БОЛАДЫ?
А) А> 2; Ә) А≥ 2; Б) А< 2; В) А ≤ 2
4. БІР ЖАЗЫҚТЫҚТА ЖАТАТЫН БІР-БІРІМЕН
ҚИЫЛЫСПАЙТЫН ЕКІ ТҮЗУ ........ ДЕП
АТАЛАДЫ
А) КЕСІНДІ; Ә) ПЕРПЕНДИКУЛЯР; Б)
ЖАЗЫҚТЫҚ; В) ПАРАЛЛЕЛЬ
ТЕСТ
II НҰСҚА
1. [5; 9] САН АРАЛЫҒЫНЫҢ АТЫ;
А) КЕСІНДІ, Ә) СӘУЛЕ, Б) АШЫҚ СӘУЛЕ, В)
ИНТЕРВАЛ
2. БЕЛГІЛЕНУІМЕН ЖАЗ: 2-ДЕН 7-ГЕ ДЕЙІНГІ
ИНТЕРВАЛ
А) [2; 7], Ә) ( 2; 7], Б) [ 2; 7), В) (2; 7)
3. Х-ТІҢ ҚАНДАЙ МӘНДЕРІНДЕ БӨЛШЕГІ
БҰРЫС БӨЛШЕК БОЛАДЫ
А) Х<3,25; Ә) Х≤ 3,25; Б) Х> 3,25; В) Х≥ 3,25
4. ТІК БҰРЫШТЫ КООРДИНАТАЛАР ЖҮЙЕСІ
ОРНАЛАСҚАН ЖАЗЫҚТЫҚ ........ ДЕП
АТАЛАДЫ.
А)КООРДИНАТАЛЫҚ ЖАЗЫҚТЫҚ; Б)
КООРДИНАТАЛАР БАСЫ; Ә)АБСЦИССА В)
Тақырыпты ашып
алу
Парақ бетіне а түзуін сызып, оның
бойымен парақты бүктеңдер.
Бүктелген парақтың сыртқы бетіне
қандай да бір өрнектің жартысының
суретін салыңдар.
Қағаздағы салынған суретті
қайшымен қиып алыңдар. Қағаздың
бүктеуін жазыңдар. Сонда қандай
сурет алынды?
Егер түзу бойымен бүктегенде жазықтықтағы екі фигура
бір-бірімен беттесетін болса, ондай фигуралар түзуге
қатысты симметриялы фигуралар деп аталады
Симметриялы фигуралар өзара тең болады.

Егер түзу фигураны симметриялы екі бөлікке бөлсе, онда
ондай фигура осьтік симметриялы фигура деп аталады.
Түзу сол фигураның симметрия осі деп аталады.
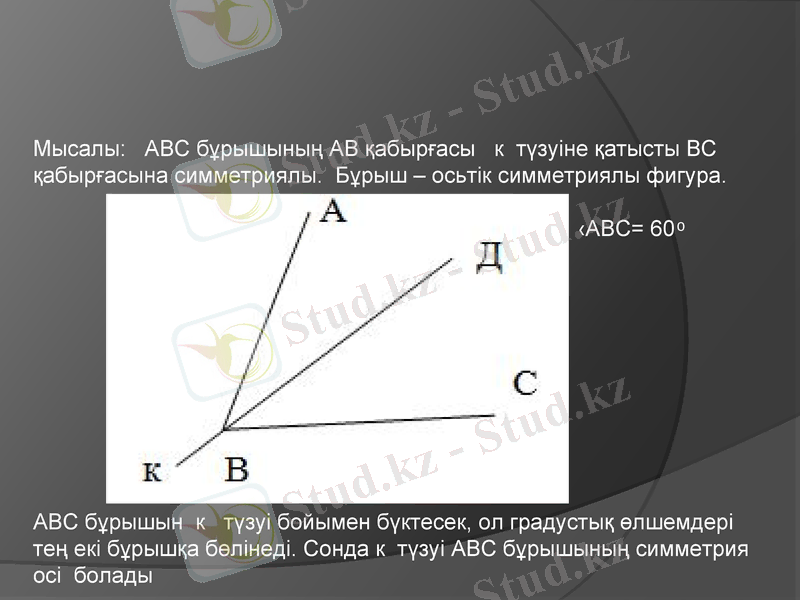
Мысалы: АВС бұрышының АВ қабырғасы к түзуіне қатысты ВС
қабырғасына симметриялы. Бұрыш – осьтік симметриялы фигура.

‹АВД=30 ‹ДВС=30 ‹АВС= 60

АВС бұрышын к түзуі бойымен бүктесек, ол градустық өлшемдері
тең екі бұрышқа бөлінеді. Сонда к түзуі АВС бұрышының симметрия
осі болады
Симметрияның екінші түрі – нүктеге қатысты симметрия.
Егер О нүктесіне қатысты симметриялы нүктелер фигураның
өзінде жатса, ол фигура центрлік симметриялы фигура деп
аталады
О нүктесі фигураның симметрия центрі деп аталады.

Шеңбер, кесінді, тік төртбұрыш – центрлік симметриялы
фигура.
Координаталық жазықтықтағы координаталар басы О
нүктесіне қатысты симметриялы нүктелердің координаталары
қарама-қарсы сандар болады.
І Т У
Р Г
Е
С ӘТ І
С
ОҚУЛЫҚПЕ
Н ЖҰМЫС:

№ 1170.
№ 1195
ТАЛДАУ
1) Қандай фигуралар түзуге
қатысты симметриялы
фигуралар деп аталады?
2) Осьтік симметриялы
фигура деп қандай фигураны
айтамыз?
3) Қандай фигуралар
центрлік симметриялы деп
аталады?
ЖИНАҚТАУ
Осьтік симметрия және центрлік
симметрияның ұқсастығымен
айырмашылығы неде?
Симметриялы фигуралар өзара тең болады.
Бұрыш – осьтік симметриялы фигура
Тік төртбұрыш, квадрат, шеңбер – осьтік
симметриялы фигуралар.
Тік төртбұрыш, шеңбер, кесінді – центрлік
симметриялы фигуралар.
ҮЙ ЖҰМЫСЫ:

№1171, 1172

Ұқсас жұмыстар

Инерция моменті Инерция тензоры

САЛУ ЕСЕПТЕРІН ШЕШУ ӘДІСТЕМЕСІ

Рационал сандарды азайту

Өсімдіктердің өсімді мүшелері

Инверсия және шеңберлер

Пәндер