Презентациялар

Функцияның экстремумдері мен сындық нүктелерін туынды таңбасымен анықтау

Сындық нүктелер.

Функцияның экстремумдері.

Абыз ата

Сабақ кезеңдері

Білгендерден ғибрат ал,

Білгеніңді сөйлеп қал

Шапқан озар, жатқан қалар.

Білгенің бір тоғыз,

Білмегенің тоқсан тоғыз.

Асу бермес асқар жоқ.

Талапты ерге нұр жауар.

Жеті жұрттың тілін біл,

Жеті түрлі білім ал.

Білімнің басы бейнет,

Соңы зейнет.

Тоқсан ауыз сөздің,

Тобықтай түйіні бар.

Әдепсіз өскен баладан, Тәртіппен өскен тал жақсы.

Ауызша сұрақтар

-Өспелі және кемімелі функцияның анықтамасы. -Функцияның өсуі мен кемуінің жеткілікті шарты. -Қандай функцияны бірсарынды деп атаймыз? -Функцияның өсу және кему аралықтарын анықтау алгоритмі

Сәйкестендіру тесті

Функция

1) у = х³ + х

2) у = 3х + 5х + 6

3) y = 5x³

4) y = 4sin 3x

5) y = x³ + 4x + 3

6) y = (3 + 4x) (4x - 3)

Туындысы

15 x²

3x² + 1

12х³+ 5

3x² + 4

32x

12 cos 3x

4

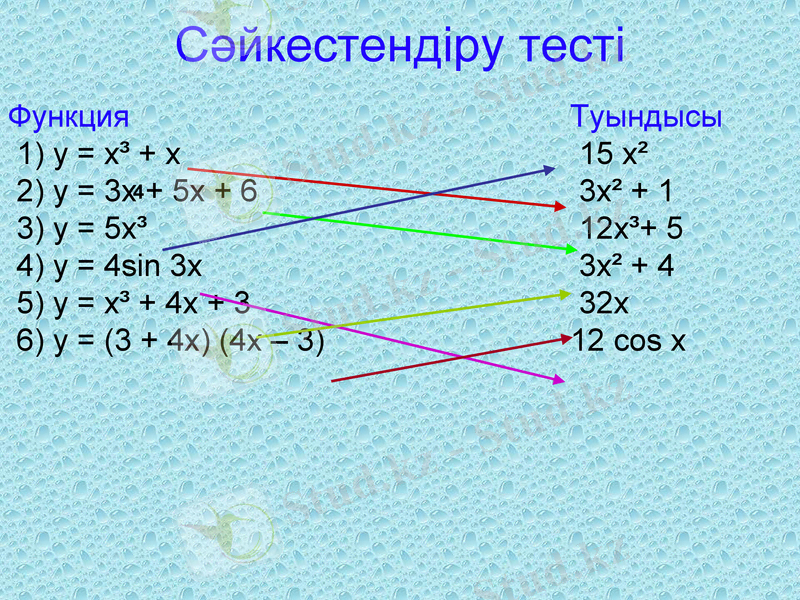
Сәйкестендіру тесті

Функция

1) у = х³ + х

2) у = 3х + 5х + 6

3) y = 5x³

4) y = 4sin 3x

5) y = x³ + 4x + 3

6) y = (3 + 4x) (4x - 3)

Туындысы

15 x²

3x² + 1

12x³+ 5

3x² + 4

32x

12 cos x

4

Анықтама

Функцияның туындысы нөлге тең немесе туындысы болмайтын анықталу облысының ішкі нүктелері сындық нүктелер деп аталады

Экстремум болуының қажетті шарты

Егер f(x) функциясының х экстремум нүктесі болып және осы нүктенің аймағында f `(x) туындысы бар болса, онда ол туынды х нүктесінде нөлге тең, яғни f `(x ) =0

у = 1 - х²

у = х³

у = x

y =³√x

y`= - 2х

у`= 3х²

1, х > 0

-1, х < 0

1

3³√x²

у`(0) = 0

у`(0) = 0

у`(0) жоқ

у`(0) жоқ

экстремум

бар

экстремум

жоқ

экстремум

бар

экстремум

жоқ

у

х

у

х

х

у

х

у

У ` =

у `= -

у = 1 -х²

у = х³

у = x

у = ³√x

Туынды таңбасы

у`:“+” → “-”

х = 0

у`:“+” → “+”

х = 0

у`:“-” → “+”

х = 0

у`:“+” → “+”

х = 0

х = 0 -

максимум

нүктесі

Экстремум

жоқ

х = 0 -

минимум

нүктесі

Экстремум

жоқ

Экстремумның бірінші жеткілікті шарты.

у=ƒ(х) функциясы х нүктесінде үзіліссіз және қандай да бір δ-маңайында функция туындысы бар болсын (х ) нүктесінде туынды болмауы мүмкін . Онда,

1) егер х аргумент х нүкте арқылы өткенде ƒ`(х) таңбасын оңнан теріске өзгертсе, онда х нүкте максимум нүктесі болады;

2) егер х аргумент х нүкте арқылы өткенде ƒ`(х) таңбасын терістен оңға өзгертсе, онда х нүкте минимум нүктесі болады;

3) егер х аргумент х нүкте арқылы өткенде ƒ`(х ) таңбасын өзгертпесе, онда х нүкте экстремум нүктесі емес.

/’

Функцияның экстремум нүктелерін табу алгоритмі.

Функцияның туындысын табу.

Функцияның сындық нүктелерін табу.

Сындық нүктелер аймағында туындының таңбасын интервалдар әдісімен аңықтау.

Максимум және минимум нүктелерін табу.

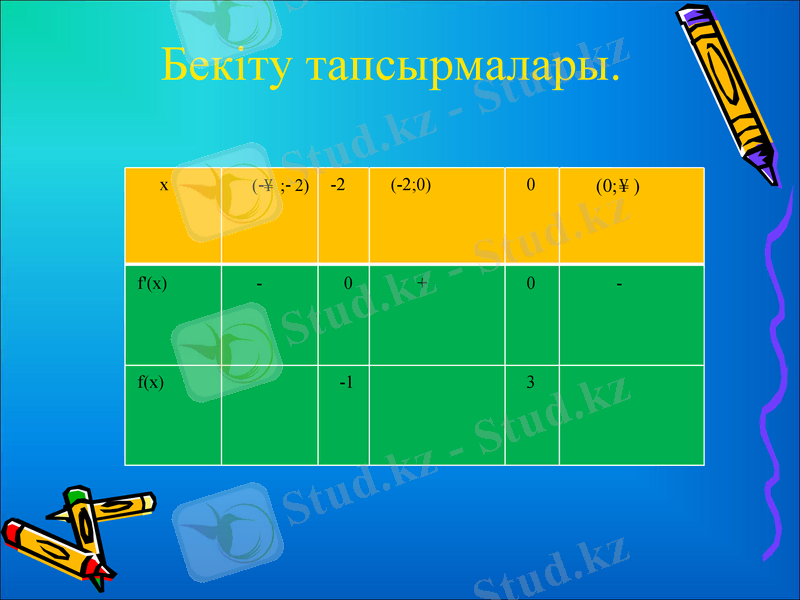
Бекіту тапсырмалары.

х

-2

(-2; 0)

0

f'(х)

-

0

+

0

-

f(х)

-1

3

х

( -7; 1)

1

(1; 6)

6

(6; 7)

f'(х)

+

0

-

0

+

f(х)

10

-3

х

(-3; 0)

0

(0; 4)

4

( 4; 8)

8

f'(х)

+

0

-

0

+

0

-

f(х)

-3

-5

6

ҰБТ - ы уақыты

Үй тапсырмасы: §20. Теореманы білу. №227 № 232

Сабақ кезеңдері

Білгендерден ғибрат ал,

Білгеніңді сөйлеп қал

Шапқан озар, жатқан қалар.

Білгенің бір тоғыз,

Білмегенің тоқсан тоғыз.

Асу бермес асқар жоқ.

Талапты ерге нұр жауар.

Жеті жұрттың тілін біл,

Жеті түрлі білім ал.

Білімнің басы бейнет,

Соңы зейнет.

Тоқсан ауыз сөздің,

Тобықтай түйіні бар.

Әдепсіз өскен баладан, Тәртіппен өскен тал жақсы.

Ұқсас жұмыстар

Функцияның сындық және экстремум нүктелері: анықтамалар мен табу алгоритмі

Бір айнымалы функцияның дифференциалдық есептеулері: туынды, дифференциалдау ережелері, айқындалмаған функциялардың туындылары және жоғары реттік туындылар

Туынды ұғымы және экономикалық талдаудағы қолданылуы

Функцияның үзіліссіздігі және үзіліс нүктелерінің жіктелуі

Туынды тақырыбына арналған есептер мен жаттығулар

Қазақ тіліндегі сындық және сандық фразеологизмдердің семантикасы

Туынды табу ережелері мен күрделі және дербес туындыларды есептеу

Сызықтық функцияның графигі: сабақ жоспары

Параметрлік функциялар, жоғары ретті туындылар мен дифференциалдар және айқындалмаған функцияның туындысы

Туынды ұғымын оқып үйренуде тарихи мағлұматтарды қолдану

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz