Математикалық және алгебралық логиканың негіздері: операциялар, заңдар және шындық кестелері



ДК Логикалық негізі
Математикалық логиканың түсініктемесі
Қарапайым логикалық операциялар
Алгебралық логиканың негізгі заңдары

Логика - (гр. λογική - «талдауға құрылған», λόγος - «сөз», «сөйлем», «ойлау», «ақыл») - ойлау, оның формалары мен заңдылықтары туралы ғылым. Логика дәлелдеу мен теріске шығарудың белгілі бір әдіс-тәсілдері қаралатын ғылым теориялар жиынтығын құрайды.

Алгебралық логика
зерттеулер дәлелдер мен құндылықтар екі элементтерін (мысалы, {0, 1}) берілген жиынтығы тиесілі функцияларын қасиеттері.
Кейде, оның орнына «термині алгебра логикасы» атты «екілік логикалық» термині «бинарлық логика» қолданылады.

Тарих
Аристотель (IV век до н. э) -
формальды логиканың пайда болуы
Лейбниц (XVII век) -
математикалық (символикалық) логиканың пайда болуы.
Лейбниц Готфрид Вильгельм
Аристотель

Дж. Буль (1815-1864)
Алгебралық логикасының атасы XIX ғасырдағы Джордж Буль болып саналады. Ол алгебрадағы формальды логикасының секцияларын бірін салған.
К. Шеннон (1916-2001)
Ұзақ уақыт бойы алгебралық логика мамандар үшін тар белгілі болды. Дж. Ьульдің алгебралық логиканы шығарғанан 100 жыл өтті. Бірақ та 1938 жылы амрекандық математигі әрі инженері Клод Шеннон бинарлық логика әртурлі процесстерде қолдана алатындығын көрсетті, сонымен қоса электронды-құбырлар тізбектер
Шеннон Клод Элвуд
Джордж Буль

Анықтама
Логика - ойлау нысандары мен тәсілдерін туралы ғылым

Ұғым - Нысанның негізгі, маңызды ерекшеліктерін бекіту ойлау формасы.
Есеп бекіту -ойлау формасы. Біз нысандар арасында өзара қарым-қатынас орнату қасиеттері тұжырымдамалармен. Ол барабар осы қарым-қатынасты көрсетеді, егер есеп рас әйтпесе жалған
Қорытынды - бір немесе бірнеше пайымдаулар (сәлемдемелер) жаңа ұсыныстар (қорытынды) арқылы алуға болады, ойлау формасы

Есеп бекіту
Есеп бекіту - нәрсе нақты объектілерін, олардың қасиеттері және олардың арасындағы қарым-қатынас туралы бекітілген немесе жоққа, ойлау формасы;
Есеп бекіту ақикат немесе жалған болуы мүмкін;
Есеп бекіту табиғи және ресми тілдерді арқылы білдіруге болады;
Есеп бекіту тек декларативтік сөйлем білдірді болады;
Есеп бекіту қарапайым немесе құрама болуы мүмкін;
Қарапайым ақиқат есеп бекітуі ой негізінде анықталады;
Құрама ақиқат есеп бекітуі алгебра пайдалана отырып айқындалады.

Ақиқат туралы
Мысалы. «Сан 1 +2 32= 4294967297 - қарапайым», Ферма (1601-1665), көп уақыт бойы ақиқат болып саналған, бірақ1732 жылы Эйлер (1707-1783) бұл сан жалған екенін дәлелдеді.

(Аристотель) .
Логикалық есеп - бұл айтуға болады, оған қатысты кез келген декларативтік сөйлем болып табылады, ол шын немесе жалған

Логикалық байланыс
Логикалық операцияның аты
Белгіленуі
Жоқ
Терістеу
‾ ¬
Және
Конъюнкция
& ^ *
Немесе
Дизъюнкция = логическое сложение
V +
Егер…онда
Импликация = следование
Сонда тек қана сонда
Эквивалентность
≡ ~

Алгебралық логика құрылымы (пішіні, құрылымы) күрделі логикалық мәлімдемелер және қалай алгебралық әдістерді қолдана отырып олардың шындықты құру.

Қарапайым логикалық оперциялар
Терістеу
Конъюнкция
Дизъюнкция
Импликация
Эквивалентілік
Штрих Шеффера
Пирс сызығы
Переход к разделу «Законы логики»

A
Ā
0
1
1
0
А - лампа жанады Ā -Терістеу?
11 санап оқушылары жақсы оқуда

Конъюнкция “және”
F = A · B=A Λ B=A & B (логикалық көбейту)
F
A
B
A
B
F
0
1
2
3
0
0
1
1
0
1
0
1
0
0
0
1
А - Ертен аяз болады
В - Ертен қар жауады
F ?
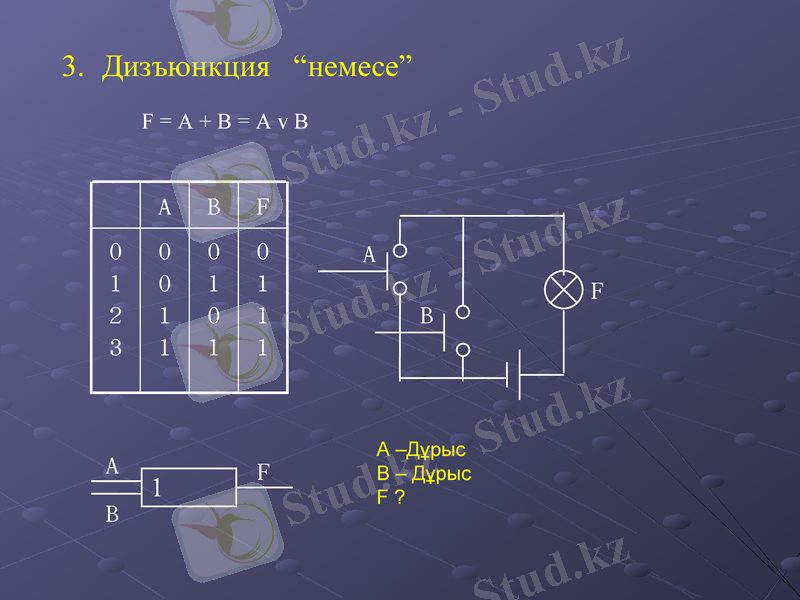
Дизъюнкция “немесе”
F = A + B = A v B
A
B
F
0
1
2
3
0
0
1
1
0
1
0
1
0
1
1
1
F
A
B
А -Дұрыс
В - Дұрыс
F ?

Импликация “егер…онда”
F = A → B = Ā v В
A
B
F
0
1
2
3
0
0
1
1
0
1
0
1
1
1
0
1

Эквивалентілік “сонда тек қана сонда” математикада- «қажетті және жеткілікті»
F = A ↔ Е = (Ā + Е) * (А + Ē)
Егер А және В сәкес келсе, онда ол жалған болады.
A
Е
F
0
1
2
3
0
0
1
1
0
1
0
1
1
0
0
1

A
B
F
0
1
2
3
0
0
1
1
0
1
0
1
1
1
1
0

A
B
F
0
1
2
3
0
0
1
1
0
1
0
1
1
0
0
0
Меню выбора операций

Логикалық заңдар
x ≡ x
x · x = 0
x + x = 1
x = x Екілік терістеу
x · x = x идемпотентілік заңы x + x = x
x · y = y · x коммутативтік заңы
x + y = y + x
x · y · z = x · ( y · z ) ассоциативтік заңы
x + y + z = x + ( y + z )
x · ( y +z ) = x · y + x · z дистрибутивтік заңы
x + ( y · z) = ( x + y ) ( x + z )
x · y = x + y Де Морган заңы
x + y = x · y
=


Ақақат кестесі
x
y
x
y
xy
xy
F
0
0
1
1
0
0
0
0
1
1
0
0
1
1
1
0
0
1
1
0
1
1
1
0
0
0
0
0
x
y
F
0
0
0
0
1
1
1
0
1
1
1
0
1-ші жол
2-ші жол

Тест сұрақтары
1) Алгебралық логикасының атасы кім? A) Дж. Буль B) Шенон C) Аристотель D) Пифагор E) Лейбниц

2) x · y = y · x x + y = y + x каңдай заң?
A) Жұту
B) Де Морган
C) ассоциативтік
D) Коммутативтік
E) Дұрыс жауабы жоқ

3) F=AB=A·B=A+B ?
A) Шеффер сызығы
B) Коньюкция
C) Дизьюнкция
D) Эквиваленттік
E) Дұрыс жауабы жоқ

4) Формальды логика дегеніміз не?
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz